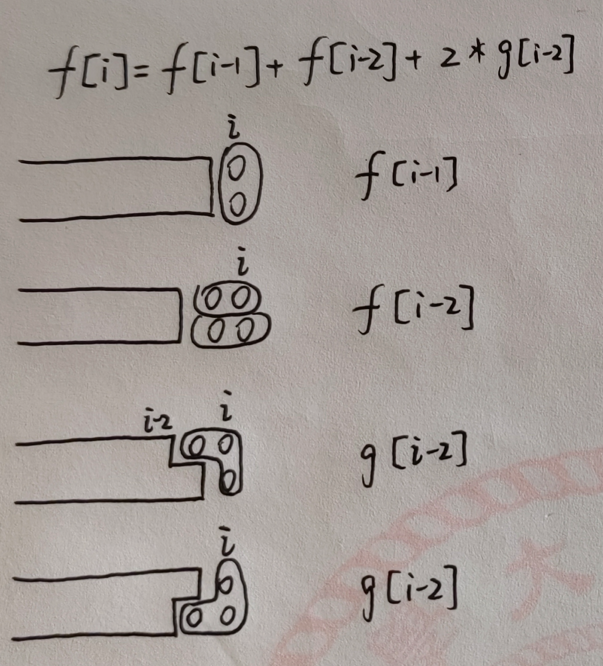进阶算法

前言¶

本文记录进阶算法的「例题解析」。

动态规划¶

动态规划的「例题解析」。

动态规划分为被动转移和主动转移，而其根本在于状态表示和状态转移。如何完整表示所有状态？如何不重不漏划分子集从而进行状态转移？

递推¶

反转字符串：https://www.acwing.com/problem/content/5574/

题意：给定 n 个字符串，每一个字符串对应一个代价 \(w_i\)，现在需要对这 n 个字符串进行可能的翻转操作使得最终的 n 个字符串呈现字典序上升的状态，给出最小翻转代价。

思路：很显然每一个字符串都有两种状态，我们可以进行二叉搜索或者二进制枚举。那么我们可以进行 dp 吗？答案是可以的。我们可以发现，对于第 i 个字符串，是否需要翻转仅仅取决于第 i-1 个字符串的大小，无后效性，可以进行递推。我们定义状态数组 f[i][j] 进行状态标识。其中

f[i][0] 表示第 i 个字符串不需要翻转时的最小代价

f[i][1] 表示第 i 个字符串需要翻转时的最小代价

状态转移就是当前一个字符串比当前字符串的字典序小时进行转移，即当前最小代价是前一个状态的最小代价加上当前翻转状态的代价。至于什么时候可以进行状态转移，一共有 4 种情况，即：

s[i-1] 不翻转，s[i] 不翻转。此时 f[i][0] = min(f[i][0], f[i-1][0])

s[i-1] 翻转，s[i] 不翻转。此时 f[i][0] = min(f[i][0], f[i-1][1])

s[i-1] 不翻转，s[i] 翻转。此时 f[i][1] = min(f[i][1], f[i-1][0] + w[i])

s[i-1] 翻转，s[i] 翻转。此时 f[i][1] = min(f[i][1], f[i-1][1] + w[i])

最终答案就在 f[n][0] 和 f[n][1] 中取 min 即可

时间复杂度：\(O(n)\)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
using ll = long long;

const int N = 100010;

int n, w[N];
string s[N][2];  // s[i][0] 表示原始字符串，s[i][1] 表示反转后的字符串
ll f[N][2];      // f[i][j] 表示第i个字符串在翻转状态为j的情况下的最小代价

ll dp() {
    f[1][0] = 0, f[1][1] = w[1];
    for (int i = 2; i <= n; i++) {
        if (s[i - 1][0] <= s[i][0]) f[i][0] = min(f[i][0], f[i - 1][0]);
        if (s[i - 1][1] <= s[i][0]) f[i][0] = min(f[i][0], f[i - 1][1]);
        if (s[i - 1][0] <= s[i][1]) f[i][1] = min(f[i][1], f[i - 1][0] + w[i]);
        if (s[i - 1][1] <= s[i][1]) f[i][1] = min(f[i][1], f[i - 1][1] + w[i]);
    }
    return min(f[n][0], f[n][1]);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    for (int i = 1; i <= n; i++) {
        cin >> s[i][0];
        s[i][1] = s[i][0];
        reverse(s[i][1].begin(), s[i][1].end());
    }
    memset(f, 0x3f, sizeof f);

    ll res = dp();
    if (res == 0x3f3f3f3f3f3f3f3fll) res = -1;
    cout << res << "\n";

    return 0;
}

最大化子数组的总成本：https://leetcode.cn/problems/maximize-total-cost-of-alternating-subarrays/

题意：给定长度为 n 的序列，现在需要将其分割为子数组，并定义每一个子数组的价值为「奇数位置为原数值，偶数位置为相反数」，返回最大分割价值

思路：~~一开始还在想着如何贪心，即仅考虑连续的负数区间，但是显然的贪不出全局最优解。~~于是转而考虑暴力 dp。思路和朴素 01 背包有相似之处。

状态定义。首先我们一定需要按照元素进行枚举，因此第一维度我们就定义为序列长度，但是仅仅这样定义就能表示全部的状态了吗？显然不行。根据题目的奇偶价值约束，我们在判定每一个负数是否可以「取相反数」价值时，是取决于上一个负数是否取了相反数价值。为了统一化，我们将正负数一起考虑前一个数是否取了相反价值的情况，因此我们需要再增加「前一个数是否取了相反价值」的状态表示，而这仅仅是一个二值逻辑，直接开两个空间即可。于是状态定义呼之欲出：

f[i][0] 表示第 i 个数取原始价值的情况下，序列 [0, i-1] 的最大价值

f[i][1] 表示第 i 个数取相反价值的情况下，序列 [0, i-1] 的最大价值

状态转移。显然对于上述状态定义，仅仅需要对「连续负数区间」进行考虑，因此对于 nums[i] >= 0 的情况是没有选择约束的，原始价值和相反价值都是可行的方案那么为了最大化最终收益显然选择原始正价值，并且可以从上一个情况的任意状态转移过来那么同样为了最大化最终受益显然选择最大的基状态，于是可得：

f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]

f[i][1] = max(f[i-1][0], f[i-1][1]) - nums[i]

而对于 nunms[i] < 0 的情况，能否选择相反数取决于前一个数的正负性。当前一个数 nums[i-1] >= 0 时，显然当前负数原始价值和相反价值都可以取到；当前一个数 nums[i-1] < 0 时，则当前负数仅有在前一个负数取原始价值的情况下才能取相反价值，于是可得：

if nums[i-1] >= 0

f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]

f[i][1] = max(f[i-1][0], f[i-1][1] - nums[i])

if nums[i-1] < 0

f[i][0] = max(f[i-1][0], f[i-1][1] + nums[i])

f[i][1] = f[i-1][0] - nums[i]

答案表示。max(f[n-1][0], f[n-1][1])

时间复杂度：\(O(n)\)

class Solution {
public:
    long long maximumTotalCost(vector<int>& nums) {
        using ll = long long;

        int n =  nums.size();

        vector<vector<ll>> f(n, vector<ll>(2, 0));
        f[0][0] = f[0][1] = nums[0];
        for (int i = 1; i < n; i++) {
            if (nums[i] >= 0 || nums[i-1] >= 0) {
                f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i];
                f[i][1] = max(f[i-1][0], f[i-1][1]) - nums[i];
            } else {
                f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i];
                f[i][1] = f[i-1][0] - nums[i];
            }
        }

        return max(f[n-1][0], f[n-1][1]);
    }
};

class Solution:
    def maximumTotalCost(self, nums: List[int]) -> int:
        n = len(nums)

        f = [[0] * 2 for _ in range(n)]
        f[0][0] = f[0][1] = nums[0]
        for i in range(1, n):
            if nums[i] >= 0 or nums[i-1] >= 0:
                f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]
                f[i][1] = max(f[i-1][0], f[i-1][1]) - nums[i]
            else:
                f[i][0] = max(f[i-1][0], f[i-1][1]) + nums[i]
                f[i][1] = f[i-1][0] - nums[i]

        return max(f[n-1][0], f[n-1][1])

费解的开关

https://www.acwing.com/problem/content/97/

题意：给定 n 个 5*5 的矩阵，代表当前局面。矩阵中每一个元素要么是 0 要么是 1，现在需要计算从当前状态操作到全 1 状态最少需要几次操作？操作描述为改变当前状态为相反状态后，四周的四个元素也需要改变为相反的状态

思路：我们采用递推的思路。为了尽可能少的进行按灯操作，我们从第二行开始考虑，若前一行的某一元素为 0，则下一行的同一列位置就需要按一下，以此类推将 \(2 \to 5\) 行全部按完。现在考虑两点，当前按下状态是否合法？当前按下状态是是否最优？ 1. 对于第一个问题：从上述思路可以看出，\(1 \to n-1\) 行一定全部都是 1 的状态，但是第 \(n-1\) 行不一定全 1，因此不合法状态就是第 \(n-1\) 行不全为 1 2. 对于第二个问题：可以发现，上述算法思路中，对于第一行是没有任何操作的（可以将第一行看做递推的初始化条件），第一行的状态影响全局的总操作数，我们不能确定不对第一行进行任何操作得到的总操作数就是最优的，故我们需要对第一行 5 个灯进行枚举按下。我们采用 5 位二进制的方法对第一行的 5 个灯进行枚举按下操作，然后对于当前第一行的按下局面（递推初始化状态）进行 \(2 \to n\) 行的按下递推操作。对于每一种合法状态更新最小的操作数即可

时间复杂度：\(O(T \times 2^5 \times 25 \times 5)\)

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 10;

char g[N][N], now[N][N];
int dx[] = {0, 1, -1, 0, 0}, dy[] = {0, 0, 0, 1, -1};

void turn(int x, int y) {
    for (int k = 0; k < 5; k++) {
        int nx = x + dx[k], ny = y + dy[k];
        now[nx][ny] ^= 1;
    }
}

void solve() {
    for (int i = 1; i <= 5; i++) {
        cin >> (g[i] + 1);
    }

    int res = 30;

    for (int op = 0; op < (1 << 5); op++) {
        memcpy(now, g, sizeof g);
        int step = 0;

        // 统计第 1 行的按下次数
        for (int i = 0; i < 5; i++) {
            if (op & (1 << i)) {
                step++;
                turn(1, 5 - i);
            }
        }

        // 统计 2 ~ 5 行的按下次数
        for (int i = 1; i <= 4; i++) {
            for (int j = 1; j <= 5; j++) {
                if (now[i][j] == '0') {
                    step++;
                    turn(i + 1, j);
                }
            }
        }

        // 判断当前操作方案是否合法
        bool ok = true;
        for (int j = 1; j <= 5; j++) {
            if (now[5][j] == '0') {
                ok = false;
            }
        }

        // 若当前操作方案合法则更新最小操作次数
        if (ok) {
            res = min(res, step);
        }
    }

    cout << (res > 6 ? -1 : res) << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
    cin >> T;
    while (T--) solve();
    return 0;
}

Decode

https://codeforces.com/contest/1996/problem/E

标签：递推/线性dp/哈希

题意：给定一个01字符串，问所有区间中01数量相等的子串总共有多少个。

思路：

我们可以最直接的想到 \(O(n^5)\) 的暴力做法，即 \(O(n^2)\) 枚举区间的左右端点，\(O(n^2)\) 枚举区间中子串的左右端点，最后 \(O(n)\) 进行检查计数。当然可以用前缀和优化掉 \(O(n)\) 的检查计数。但这样做显然无法通过 \(10^5\) 的数据量。考虑别的思路。

容易想到动态规划的思路。我们定义 dp[i] 表示右端点是 s[i] 的所有区间中，合法01子串的数量，那么显然 dp[0] = s[i] == '1'。现在考虑 dp[i] 如何转移。不难发现以 s[i] 为右端点的所有区间一定包含以 s[i - 1] 为右端点的所有区间，多出来的合法子串进存在于以 s[i] 结尾的子串中，我们假设以 s[i] 结尾的合法子串数量为 t，则状态转移方程为：dp[i] = dp[i - 1] + t。显然我们可以用一个滚动变量来代替 dp 数组，记作now，每次维护完 now 以后，将其累加到答案即可。现在我们将枚举区间从 \(O(n^2)\) 通过递推的思路优化到了 \(O(n)\)。那么如何求解递推式中的 t 呢？

通过一个小 trick 求解「以 s[i] 结尾的合法子串」的数量。显然可以通过前缀和枚举 \(j \in [1,i]\) 统计使得 i - j + 1 == 2 * (pre[i] - pre[j - 1]) 的数量。但是这样就是 \(O(n^2)\) 的了，仍然无法通过本题。引入 trick：我们稍微修改一下前缀和的维护逻辑，即当 s[i] == '0' 时，将其记作 -1，当 s[i] == '1' 时，保持不变仍然记作 1。这样我们在向前枚举 j 寻找合法区间时，本质上就是在寻找 pre[i] - pre[j - 1] == 0，即 pre[j - 1] == pre[i] 的个数。假设下标从 0 开始，则每找到一个合法的 j，都会对答案贡献 j + 1。因此我们只需要哈希存储每一个前缀和对应的下标累计值即可。

时间复杂度：\(O(n)\)

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

void solve() {
    string s;
    cin >> s;

    int n = s.size();
    vector<ll> pre(n + 1);
    for (int i = 0; i < n; i++) {
        pre[i + 1] = pre[i] + (s[i] == '0' ? -1 : 1);
    }

    auto add = [&](ll x, ll y) {
        ll mod = 1e9 + 7;
        return ((x % mod) + (y % mod)) % mod;
    };

    ll res = 0, now = 0;
    unordered_map<ll, ll> f;
    for (ll i = 0; i <= n; i++) {
        now = add(now, f[pre[i]]);
        res = add(res, now);
        f[pre[i]] += i + 1;
    }

    cout << res << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
    std::cin >> T;
    while (T--) solve();
    return 0;
}

Squaring

https://codeforces.com/contest/1995/problem/C

标签：递推、数学

题意：给定一个序列，可以对其中任何一个数进行任意次平方操作，即 \(a_i \to a_i^2\)，问最少需要执行多少次操作可以使得序列不减。

思路：

首先显然的我们不希望第一个数 \(a_0\) 变大，因此我们应该从第二个数开始和前一个数进行比较，从而进行可能的平方操作并计数。但是由于数字可能会很大，使用高精度显然会超时，而这些数字本身的意义是用来和前一个数进行大小比较的，并且变化的形式也仅仅是平方操作。我们不妨维护其指数，这样既可以进行大小比较，也不用存储数字本身而造成溢出。当然变为使用指数存储以后如何进行大小比较以及如何维护指数序列有所不同，我们先从一般的角度出发，进而从表达式本身的数学角度讨论特殊情况的处理。

对于当前数字 \(a_i\) 和前一个数字 \(a_{i-1}\) 及其指数 \(z_{i-1}\)，如果想要当前数字经过可能的 k 次平方操作后不小于前一个数，即 \(\displaystyle a_{i-1}^{2^{z_{i-1}}}\le a_i^{2^{k}}\)，则易得下面的表达式：

\[ k:= z_{i-1}+ \left\lceil \log_2(\frac{\log_2 {a_{i-1}}}{\log_2{a_i}}) \right \rceil \]

由于 \(a_j \in [1, 10^6],z_j\ge 0,k \ge 0\)，因此我们有必要：

讨论 \(a_i\) 和 \(a_{i-1}\) 和 \(1\) 的大小关系。因为它们的对数计算结果在真数部分。

讨论 \(k\) 和 \(0\) 的大小关系。因为一旦 \(a_{i-1} < a_i\)，则有可能出现计算结果为负的情况，这种情况表明需要对当前数 \(a_i\) 进行开根的操作。又由于 \(a_i\ge1\)，因此开根操作就表明减小当前的数，也就表明当前数在不进行平方操作的情况下就已经满足不减的条件了，也就不需要操作了。此时对应的指数 \(z_i\) 就是 \(0\)，对于答案的贡献也是 \(0\)。

时间复杂度：\(O(n)\)

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

void solve() {
    int n;
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<ll> z(n, 0);
    ll res = 0;
    for (int i = 1; i < n; i++) {
        if (a[i] == 1 && a[i - 1] > 1) {
            cout << -1 << "\n";
            return;
        } else if (a[i] == 1 && a[i - 1] == 1 || a[i - 1] == 1) {
            continue;
        }
        ll t = z[i - 1] + ceil(log2(log2(a[i - 1]) / log2(a[i])));
        z[i] = max(0ll, t);
        res += z[i];
    }

    cout << res << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
    std::cin >> T;
    while (T--) solve();
    return 0;
}

from typing import List, Tuple
from collections import defaultdict, deque
from itertools import combinations, permutations
import math, heapq, queue

II = lambda: int(input())
FI = lambda: float(input())
MII = lambda: tuple(map(int, input().split()))
LII = lambda: list(map(int, input().split()))


def solve() -> None:
    n = II()
    a = LII()

    z = [0] * n
    for i in range(1, n):
        if a[i] == 1 and a[i - 1] > 1:
            print(-1)
            return
        elif a[i] == 1 and a[i - 1] == 1 or a[i - 1] == 1:
            continue
        t = z[i - 1] + math.ceil(math.log2(math.log2(a[i - 1]) / math.log2(a[i])))
        z[i] = max(0, t)

    print(sum(z))


if __name__ == '__main__':
    T = 1
    T = II()
    while T: solve(); T -= 1

牛的语言学

https://www.acwing.com/problem/content/description/5559/

标签：递推、dfs

题意：已知一个字符串由前段的一个词根和后段的多个词缀组成。词根的要求是长度至少为 5，词缀的要求是长度要么是 2, 要么是 3，以及不允许连续的相同词缀组成后段。现在给定最终的字符串，问一共有多少种词缀？按照字典序输出所有可能的词缀

思路一：搜索。很显然我们应该从字符串的最后开始枚举词缀进行搜索，因为词缀前面的所有字符全部都可以作为词根合法存在，我们只需要考虑当前划分出来的词缀是否合法即可。约束只有一个，不能与后面划分出来的词缀相同即可，由于我们是从后往前搜索，因此我们在搜索时保留后一个词缀即可。如果当前词缀和上一个词缀相同则返回，反之如果合法则加入 set 自动进行字典序排序。

时间复杂度：\(O(2^{\frac{n}{2}})\)

思路二：动态规划（递推）。动规其实就是 dfs 的逆过程，我们从已知结果判断当前局面是否合法。很显然词根是包罗万象的，只要长度合法，不管什么样的都是可行的，故我们在判断当前局面是否合法时，只需要判断当前词缀是否合法即可。于是便可知当前状态是从后面的字符串转移过来的。我们定义状态转移记忆数组 f[i] 表示字符串 s[1,i] 是否可以组成词根。如果 f[i] 为真，则表示 s[1,i] 为一个合法的词根，s[i+1,n] 为一个合法的词缀串，那么词根后面紧跟着的一定是一个长度为 2 或 3 的合法词缀。

我们以紧跟着长度为 2 的合法词缀为例。如果 s[i+1,i+2] 为一个合法的词缀，则必须要满足以下两个条件之一

s[i+1,i+2] 与 s[i+3,i+4] 不相等，即后面的后面是一个长度也为 2 且合法的词缀

s[1,i+5] 是一个合法的词根，即 f[i+5] 标记为真，即后面的后面是一个长度为 3 且合法的词缀

以紧跟着长度为 3 的哈法词缀同理。如果 s[i+1,i+3] 为一个合法的词缀，则必须要满足以下两个条件之一

s[i+1,i+3] 与 s[i+4,i+6] 不相等，即后面的后面是一个长度也为 3 且合法的词缀

s[1,i+5] 是一个合法的词根，即 f[i+5] 标记为真，即后面的后面是一个长度为 2 且合法的词缀

时间复杂度：\(O(n \log n)\) - dp 的过程是线性的，主要时间开销在 set 的自动排序上

dfs 代码

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#include <set>
using namespace std;

string s;
set<string> res;

// 当前词缀起始下标 idx，当前词缀长度 length，后方相邻的词缀 post
void dfs(int idx, int length, string post) {
    if (idx <= 5) return;

    string now = s.substr(idx, length);

    if (now == post) {
        // 不合法直接返回
        return;
    } else {
        // 合法则将当前词缀加入集合自动排序，并继续搜索接下来可能的词缀
        res.insert(now);
        dfs(idx - 2, 2, now);
        dfs(idx - 3, 3, now);
    }
}

void solve() {
    cin >> s;
    s = "$" + s;

    int tail_point = s.size();

    dfs(tail_point - 2, 2, "");
    dfs(tail_point - 3, 3, "");

    cout << res.size() << "\n";
    for (auto& str: res) cout << str << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

dp 代码

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#include <set>
using namespace std;

const int N = 50010;

string s;
set<string> res;
bool f[N]; // f[i] 表示 s[1,i] 是否可以作为词根存在

void solve() {
    cin >> s;
    s = "$" + s;

    // 字符串定义在 [1,n] 上
    int n = s.size() - 1;

    // 长度为 n 的字符串一定可以作为词根
    f[n] = true;

    for (int i = n; i >= 5; i--) {
        for (int len = 2; len <= 3; len++) {
            if (f[i + len]) {
                string a = s.substr(i + 1, len);
                string b = s.substr(i + 1 + len, len);
                if (a != b || f[i + 5]) {
                    res.insert(a);
                    f[i] = true;
                }
            }
        }
    }

    cout << res.size() << "\n";

    for (auto& x: res) cout << x << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

线性 dp¶

最小化网络并发线程分配

https://vijos.org/d/nnu_contest/p/1492

题意：现在有一个线性网络需要分配并发线程，每一个网络有一个权重，现在有一个线程分配规则。对于当前网络，如果权重比相邻的网络大，则线程就必须比相邻的网络大。

思路：我们从答案角度来看，对于一个网络，我们想知道它的相邻的左边线程数和右边线程数，如果当前网络比左边和右边的权重都大，则就是左右线程数的最大值+1，当然这些的前提是左右线程数已经是最优的状态，因此我们要先求“左右线程”。分析可知，左线程只取决于左边的权重与线程数，右线程同样只取决于右边的权重和线程数，因此我们可以双向扫描一遍即可求得“左右线程”。最后根据“左右线程”即可求得每一个点的最优状态。

void solve() {
    int n; cin >> n;
    vector<int> w(n + 1), l(n + 1, 1), r(n + 1, 1);
    for (int i = 1; i <= n; i++) {
        cin >> w[i];
    }
    for (int i = 2, j = n - 1; i <= n && j >= 1; i++, j--) {
        if (w[i] > w[i - 1]) {
            l[i] = l[i - 1] + 1;
        }
        if (w[j] > w[j + 1]) {
            r[j] = r[j + 1] + 1;
        }
    }
    int res = 0;
    for (int i = 1; i <= n; i++) {
        res += max(l[i], r[i]);
    }
    cout << res << "\n";
}

Block Sequence

https://codeforces.com/contest/1881/problem/E

题意：给定一个长为 \(n\le 2\times 10^5\) 的数组 a，问最少可以删除其中的几个元素，使得最终的数组可以被划分为连续的子数组且每一个子数组的元素个数均为「子数组首元素数值 \(-1\)」的形式。

思路：

首先可以看出，序列的首元素一定是对应子数组剩余元素的个数。我们不妨倒序枚举每一个元素并定义 f[i] 表示使数组 a[i:] 符合定义的最小删除次数，这样每次枚举到的元素都一定是所在子数组的首元素。

接下来考虑状态转移。对于当前枚举到的元素 a[i]，如果不删除，则 f[i] 将从 f[i+a[i]+1] 转移过来；如果删除，则 f[i] 将从 f[i+1] 转移过来。两者取最小值即可。

时间复杂度 \(O(n)\)

def solve() -> Optional:
    n = II()
    a = LII()
    f = [INF] * (n + 1)
    f[n] = 0
    for i in range(n - 1, -1, -1):
        f[i] = f[i + 1] + 1
        if i + a[i] + 1 <= n:
            f[i] = min(f[i], f[i + a[i] + 1])
    return f[0]

覆盖墙壁

https://www.luogu.com.cn/problem/P1990

题意：给定两种砖块，分别为日字型与L型，问铺满 \(2*n\) 的地板一共有多少种铺法

思路：

我们采用递推的思路

\(define:\) f[i] 表示铺满前 \(2*i\) 个地板的方案数，g[i] 表示铺满前 \(2*i+1\) 块地板的方案数

\(base:\) f[0] = 1, f[1] = 1, g[0] = 0, g[1] = 1

\(dp:\) f[i] = f[i-1] + f[i-2] + g[i-1] \(||\) g[i] = f[i-1] + g[i-1]

\(result:\) f[n]

手绘：

#include <bits/stdc++.h>
using namespace std;

const int N = 1000010, mod = 10000;

int n;
int f[N], g[N];

void solve() {
    cin >> n;

    // base
    f[0] = 1, f[1] = 1;
    g[0] = 0, g[1] = 1;

    // dp
    for (int i = 2; i <= n; i++) {
        f[i] = (f[i - 1] + f[i - 2] + 2 * g[i - 2]) % mod;
        g[i] = (f[i - 1] + g[i - 1]) % mod;
    }

    // result
    cout << f[n] << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

施咒的最大总伤害

https://leetcode.cn/problems/maximum-total-damage-with-spell-casting/

标签：线性 dp

题意：给定一个数组，选择一个子序列使得总和最大。约束为：如果选择了值为 \(x\) 的元素，则不允许选择值为 \(x-2,x-1,x+1,x+2\) 的元素

思路：

哈希计数。首先很显然的我们需要进行哈希计数，便于按数值升序枚举元素。我们定义哈希后的序列为 v，大小为 m，存储每一种数的数值 val: int 和个数 cnt: int

状态定义。我们定义状态 f[i] 表示哈希序列 [1,i] 中子序列总和的最大值，则最终答案就是 f[m]

状态转移。对于每一个哈希元素，都有选择和不选两种状态。假设当前枚举到的哈希元素为 i，

不选当前元素。就相当于没有当前元素，则 f[i] = f[i-1]

选择当前元素。我们就需要从哈希序列 [1,i-1] 中，比当前哈希元素 v[i].val 小 2 且对应子序列之和最大的那个状态 f[j] 转移过来。显然我们可以直接枚举哈希序列 [1,i-1]，但是这样就是 \(O(n^2)\) 必然超时，考虑优化。不难发现 f[] 数组是单调递增的并且哈希序列的元素数值 v[].val 也是单调递增的。也就是说对于当前状态 f[i]，在枚举哈希序列 [1,i-1] 时，其实并不需要从 1 开始枚举，可以从上一个状态枚举到的状态（记作 j）开始枚举（因为上一个状态对应的 f[j] 是上一个状态可转移的方案中最大的并且 v[j].val 一定比当前方案的哈希数值 v[i].val 小 2）。于是状态转移的时间开销就从 \(O(n)\) 优化到 \(O(1)\)，可以通过此题

时间复杂度：\(O(n)\)

空间复杂度：\(O(n)\)

class Solution {
public:
    long long maximumTotalDamage(vector<int>& power) {
        using ll = long long;

        // hash
        map<int, int> a;
        for (int x: power) {
            a[x]++;
        }
        int m = a.size(), idx = 1;
        struct node { ll val, cnt; };
        vector<node> v(m + 1);
        for (auto it: a) {
            v[idx++] = {it.first, it.second};
        }

        // dp
        vector<ll> f(m + 1);
        f[1] = v[1].val * v[1].cnt;
        for (int i = 2, j = 1; i <= m; i++) {
            while (j < i && v[j].val < v[i].val - 2) {
                j++;
            }
            j--;

            f[i] = max(f[i - 1], f[j] + v[i].val * v[i].cnt);
        }

        return f[m];
    }
};

class Solution:
    def maximumTotalDamage(self, power: List[int]) -> int:
        from collections import defaultdict

        # hash
        a = defaultdict(int)
        for x in power:
            a[x] += 1
        a = sorted(a.items(), key=lambda x: x[0])

        class node:
            def __init__(self, val: int, cnt: int) -> None:
                self.val = val
                self.cnt = cnt

        m, idx = len(a), 1
        v = [node(0, 0)] * (m + 1)
        for it in a:
            v[idx] = node(it[0], it[1])
            idx += 1

        # dp
        f = [0] * (m + 1)
        f[1], j = v[1].val * v[1].cnt, 1
        for i in range(2, m + 1):
            while j < i and v[j].val < v[i].val - 2:
                j += 1
            j -= 1

            f[i] = max(f[i - 1], f[j] + v[i].val * v[i].cnt)

        return f[m]

奇怪的汉诺塔

https://www.acwing.com/problem/content/98/

题意：四塔汉诺塔问题。求在给定 \(n\) 个圆盘的情况下的最少移动方案数。

思路：

我们定义「最小完成单元」为：在满足游戏规则的情况下，将一座塔的所有圆盘移动到另一座塔所需的最少塔数。那么显然的最小完成单元为 3 座塔。定义 d[i] 表示三塔模式下 \(i\) 个盘的最少移动次数，f[i] 表示四塔模式下 \(i\) 个盘的最少移动次数。

对于 4 座塔的情况，相当于最小完成单元又多了 1 座塔。那么显然多出来的这座塔有两个处置方案：

如果我们不利用这座塔。那么还剩 3 座塔，也就是最小完成单元，此时的最少移动次数是唯一的，也就是 f[i] = d[i]

如果我们要利用这座塔。那么我们只能在这一座塔上按规则放圆盘。因为要确保最小完成单元来让剩余的圆盘移动到另一座塔。如果还在别的塔上放置了圆盘，那么将不符合最小完成单元的定义，游戏无法结束。当然我们不能将所有的圆盘都先放到这座塔上，因为这种情况下是不可能成立的，我们不可能让一个「我们正在求解的问题」作为我们的答案。也就是说 \(j<i\)

至此四塔模式下 \(i\) 个圆盘游戏方案的组成集合已全部确定，如下图所示，即：在四塔模式下移动 \(j \in [0,i-1]\) 个圆盘到其中一座空塔上，方案数为 \(f[j]\)；剩余的 \(i-j\) 个圆盘处于最小完成单元的局面，方案数是唯一的 \(d[i-j]\)；最后再将一开始移动的 \(j\) 个圆盘在四塔模式下移动到刚才剩余圆盘移动到的塔上，方案数为 \(f[j]\)。

于是最终的状态转移方程为：

\[ f_i = \min{ \{ f_j+d_{i-j}+f_j \} },\quad i \in [1,n],\quad j \in [0,i-1] \]

时间复杂度：\(O(n^2)\)

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

void solve() {
    int n = 12;
    vector<int> d(n + 1);       // d[i] means move i pans to another tower with 3 towers
    vector<int> f(n + 1, 1e9);  // f[i] means move i pans to another tower with 4 towers

    d[1] = 1;
    for (int i = 1; i <= n; i++) {
        d[i] = 1 + 2 * d[i - 1];
    }
    f[1] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= i - 1; j++) {
            f[i] = min(f[i], f[j] + d[i - j] + f[j]);
        }
        cout << f[i] << "\n";
    }
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
//    std::cin >> T;
    while (T--) solve();
    return 0;
}

数的计算

https://www.luogu.com.cn/problem/P1028

题意：给定一个数和一种构造方法，即对于当前的数，可以在其后面添加一个最大为当前一半大的数，以此类推构造成一个数列。问一共可以构造出多少个这种数列

思路一：dfs

非常显然的一个搜索树，答案就是结点数

时间复杂度：\(O(\text{方案数})\)

思路二：dp

非常显然的一个dp，我们定义一个dp记忆数组。其中 dp[i] 表示数字 i 的构造方案总数，那么状态转移方程就是

\[ dp[i]=\sum_{j=1}^{\left\lfloor i/2 \right\rfloor}dp[j]+1 \]

时间复杂度：\(O(n^2)\)

dfs代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int n, res;

void dfs(int x) {
    res++;
    for (int i = x >> 1; i >= 1; i--) {
        dfs(i);
    }
}

void solve() {
    cin >> n;
    dfs(n);
    cout << res << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

dp代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int n;

void solve() {
    cin >> n;

    vector<ll> dp(n + 1, 1);
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= i >> 1; j++) {
            dp[i] += dp[j];
        }
    }

    cout << dp[n] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

规划兼职工作

https://leetcode.cn/problems/maximum-profit-in-job-scheduling/description/

标签：线性dp、二分答案

题意：给定 n 份工作的起始时间、终止时间、收益值，现在需要不重叠时间的选择工作使得收益最大

思路：动态规划、二分答案。为了不重不漏的枚举每一份工作，我们将工作按照结束时间进行排序，然后就可以枚举每一份工作了。接下来要解决的问题是，如何根据起始时间和终止时间进行工作的选择。显然的，每一份工作有选与不选两种状态，是否选择取决于收益是否更优，我们考虑动态规划。我们定义状态表 f[i] 表示在前 i 个工作中选择的最大工作收益，返回值就是 f[n]，先看图

选择第 i 个工作：f[i] = f[r] + profit[i]（其中 r 表示 [1,i-1] 份工作中，结束时间早于当前工作起始时间的最右边的工作，在 [1,i-1] 中二分查找即可）

不选第 i 个工作：f[i] = f[i - 1]

选择最大属性进行状态转移即可：f[i] = max(f[i - 1], f[r] + profit[i])

时间复杂度：\(O(n\log n)\)

class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = startTime.size();
        vector<array<int, 3>> jobs(n + 1);

        for (int i = 1; i <= n; i++) {
            jobs[i] = {startTime[i - 1], endTime[i - 1], profit[i - 1]};
        }

        sort(jobs.begin() + 1, jobs.end(), [&](array<int, 3>& x, array<int, 3>& y){
            return x[1] < y[1];
        });

        vector<int> f(n + 1);
        for (int i = 1; i <= n; i++) {
            int l = 0, r = i - 1;
            while (l < r) {
                int mid = (l + r + 1) >> 1;
                if (jobs[mid][1] <= jobs[i][0]) l = mid;
                else r = mid - 1;
            }
            f[i] = max(f[i - 1], f[r] + jobs[i][2]);
        }

        return f[n];
    }
};

最长上升子序列

https://www.luogu.com.cn/problem/B3637

标签：线性dp、二分查找

题意：给定序列，求解其中最长上升子序列 (Longest Increasing Subsequence, 简称 LIS) 的长度。

思路：我们采用动态规划。

状态定义：定义状态数组 f[i] 表示以元素 a[i] 结尾的最长上升子序列的长度，显然的初始状态全都是 1

状态转移：

暴力枚举。首先很显然的 f[i] 一定是从 [0,i-1] 中比当前元素值小的状态转移过来，于是可以很轻松的写出双重循环的代码，时间复杂度 \(O(n^2)\)。

贪心+二分优化。

回顾朴素。优化需要在理解转移本质的基础上展开，因此我们先来回顾一下朴素版的转移方案：从 [0,i-1] 中比当前元素小的元素 a[j] 对应的最长上升子序列长度 f[j] 转移过来。我们枚举了 [0,i-1] 所有的状态确保了不重不漏。对于 i = 6 来说，如下图所示。其中✔表示进入了 if 的判断逻辑。最终我们选择从 j = 5 对应的 f[j] = 3 转移而来。这里的判断准则为：对于每一个元素，需要找前面的元素中比当前元素小的元素。

转换视角。同样对于每一个元素 a[i]，我们不再按顺序枚举前面已经计算出来的 f[1:i-1]，而是预先按照长度存储所有的 f[1:i-1] 从而枚举长度 j，显然可以贪心的从最大长度 mxa_len 开始枚举。一旦遇到比 a[i] 小的元素，那么 f[i] 就等于当前枚举的长度+1，即 f[i] = j + 1。对于 i = 6 来说，如下图所示。这样也可以做到不重不漏的枚举所有状态。但是显然的，这种方法只是变相地枚举了所有的元素，仍然是 \(O(n^2)\)，并且和枚举元素相比还多了一点思维量和代码量。

优化诞生。在枚举元素时，并没有额外有价值的信息，比如元素并非单调排列，f[] 数组也并非单调。但转换到枚举长度，让我们有机会进行优化！不难发现，对于每一个元素 a[i]，我们在按长度 [1,max_len] 枚举可能的尾元素 f[1:i-1] 时，由于 max_len 每一次更新时的增量都是 1，因此 [1,max_len] 的每一个取值都一定会有对应的元素存在！贪心的，对于同一个长度下所有子序列的尾元素，我们只关心其中值最小的那一个尾元素，因此我们定义一个 mi[] 数组来存储每一个长度下子序列尾元素的最小值，其中 mi[i] 表示长度为 i 的最长上升子序列中，最小的尾元素值。这样在枚举长度 [1,max_len] 时，就不再需要枚举每一个长度下所有的尾元素，仅需枚举每一个长度下唯一的那个最小尾元素。但如果每一个长度都刚好只有一个元素，那岂不是还是需要线性枚举？更进一步的，我们可以发现，此时每一个长度对应的唯一元素组成的序列是严格单调递增的（反证法易证）！有了这样单调的性质我们就可以利用二分加速枚举，这样可以将枚举的时间复杂度严格控制在 \(O(\log n)\)。显然的，我们希望当前的元素可以拼接在尽可能长的子序列后面，因此此处的二分使用的是寻找右边界的板子。

代码实现。枚举每一个元素肯定是少不了的，我们使用 mi[j] 表示最长上升子序列长度为 j 的序列尾元素的最小值。初始状态显然就是 mi[1] = a[0]。在每一个元素二分查询「最大的比当前元素小的元素」时，如果查出来的元素 mi[r] 确实比当前元素小，则需要更新 mi[r+1] 的值；反之如果查出来的元素 mi[r] 比当前元素还小，则表明二分到了左边界，此时 r 一定是 1，直接用当前元素覆盖 mi[1] 即可。

答案表示。最终答案就是 max_len

时间复杂度：\(O(n \log n)\)

暴力枚举元素

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

void solve() {
    int n;
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<int> f(n, 1);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < i; j++) {
            if (a[i] > a[j]) {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }

    cout << *max_element(f.begin(), f.end()) << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
//    std::cin >> T;
    while (T--) solve();
    return 0;
}

暴力枚举长度

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

void solve() {
    int n;
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<vector<int>> dp(n + 1, vector<int>());
    int max_len = 1;
    dp[1].push_back(a[0]);
    for (int i = 1; i < n; i++) {
        bool ok = false;
        // 贪心的从已经出现过的最大长度开始枚举
        for (int j = max_len; j >= 1; j--) {
            // 对于当前长度下的所有元素
            for (int x: dp[j]) {
                if (a[i] > x) {
                    dp[j + 1].push_back(a[i]);
                    max_len = max(max_len, j + 1);
                    ok = true;
                    goto flag;
                }
            }
        }
        flag:
        if (!ok) {
            dp[1].push_back(a[i]);
        }
    }

    cout << max_len << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
//    std::cin >> T;
    while (T--) solve();
    return 0;
}

贪心二分优化

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

void solve() {
    int n;
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<int> mi(n + 1, INT_MAX);
    int max_len = 1;
    mi[1] = a[0];
    for (int i = 1; i < n; i++) {
        int l = 1, r = max_len;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (a[i] > mi[mid]) l = mid;
            else r = mid - 1;
        }

        if (a[i] > mi[r]) {
            mi[r + 1] = min(mi[r + 1], a[i]);
            max_len = max(max_len, r + 1);
        } else {
            // 此时长度 r 一定是 1 并且当前元素是长度为 1 的子序列尾元素中最小的
            mi[1] = a[i];
        }
    }

    cout << max_len << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
//    std::cin >> T;
    while (T--) solve();
    return 0;
}

网格图dp¶

过河卒

https://www.luogu.com.cn/problem/P1002

标签：网格图dp、dfs

题意：给定一个矩阵，现在需要从左上角走到右下角，问一共有多少种走法？有一个特殊限制是，对于图中的9个点是无法通过的。

思路一：dfs

我们可以采用深搜的方法。但是会超时，我们可以这样估算时间复杂度：对于每一个点，我们都需要计算当前点的右下角的矩阵中的每一个点，那么总运算次数就近似为阶乘级别。当然实际的时间复杂度不会这么大，但是这种做法 \(n*m\) 一旦超过100就很容易tle

时间复杂度：\(O(nm!)\)

思路二：dp

我们可以考虑，对于当前的点，可以从哪些点走过来，很显然就是上面一个点和左边一个点，而对于走到当前这个点的路线就是走到上面的点和左边的点的路线之和，base状态就是 dp[1][1] = 1，即起点的路线数为1

时间复杂度：\(O(nm)\)

dfs代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 30;

int n, m, a, b;
int res;
bool notsafe[N][N];

void init() {
    int px[9] = {0, -1, -2, -2, -1, 1, 2, 2, 1};
    int py[9] = {0, 2, 1, -1, -2, -2, -1, 1, 2};
    for (int i = 0; i < 9; i++) {
        int na = a + px[i], nb = b + py[i];
        if (na < 0 || nb < 0) continue;
        notsafe[na][nb] = true;
    }
}

void dfs(int x, int y) {
    if (x > n || y > m || notsafe[x][y]) {
        return;
    }

    if (x == n && y == m) {
        res++;
        return;
    }

    dfs(x, y + 1);
    dfs(x + 1, y);
}

void solve() {
    cin >> n >> m >> a >> b;
    init();
    dfs(0, 0);
    cout << res << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

dp代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 30;

int n, m, a, b;
bool notsafe[N][N];
ll dp[N][N];

void solve() {
    cin >> n >> m >> a >> b;

    // 初始化
    ++n, ++m, ++a, ++b;
    int px[9] = {0, -1, -2, -2, -1, 1, 2, 2, 1};
    int py[9] = {0, 2, 1, -1, -2, -2, -1, 1, 2};
    for (int i = 0; i < 9; i++) {
        int na = a + px[i], nb = b + py[i];
        if (na < 0 || nb < 0) continue;
        notsafe[na][nb] = true;
    }

    // dp求解
    dp[1][1] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (!notsafe[i - 1][j]) dp[i][j] += dp[i - 1][j];
            if (!notsafe[i][j - 1]) dp[i][j] += dp[i][j - 1];
        }
    }

    cout << dp[n][m] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

摘樱桃 II

https://leetcode.cn/problems/cherry-pickup-ii/

题意：给定一个 \(n\) 行 \(m\) 列的网格图，每个格子拥有一个价值。现在有两个人分别从左上角和右上角开始移动，移动方式为「左下、下、右下」三个方向，问两人最终最多一共可以获得多少价值？如果两人同时经过一个位置，则只能算一次价值。

思路：

状态定义。最终状态一定是两人都在最后一行的任意两列，我们如何定义状态可以不重不漏的表示两人的运动状态呢？可以发现两人始终在同一行，但是列数不一定相同，我们定义状态 \(f[i][j][k]\) 表示两人走到第 \(i\) 行时，一人在第 \(j\) 列，另一人在第 \(k\) 列时的总价值。则答案就是：

\[ \max{(f[n-1][j][k])},j,k\in[0,m] \]

状态转移。本题难点在于状态定义，一旦定义好了以后状态转移就不困难了。对于当前状态 \(f[i][j][k]\)，根据乘法原理，两人均有 3 种走法，因此当前状态可以从 \(3\times 3=9\) 种合法状态转移过来。取最大值即可。

时间复杂度：\(O(nm^2)\)

class Solution:
    def cherryPickup(self, g: List[List[int]]) -> int:
        n, m = len(g), len(g[0])
        f = [[[-1] * m for _ in range(m)] for _ in range(n)]
        f[0][0][m - 1] = g[0][0] + g[0][m - 1]
        for i in range(1, n):
            for j in range(m):
                for k in range(m):
                    # 枚举 9 个子问题
                    for p in range(j - 1, j + 2):
                        for q in range(k - 1, k + 2):
                            if 0 <= p < m and 0 <= q < m and f[i - 1][p][q] != -1:
                                f[i][j][k] = max(f[i][j][k], f[i - 1][p][q] + g[i][j] + (0 if j == k else g[i][k]))

        res = 0
        for j in range(m):
            for k in range(j, m):
                res = max(res, f[n - 1][j][k])

        return res

摘樱桃

弱化版 \((n\le 50)\) ：https://leetcode.cn/problems/cherry-pickup/

强化版 \((n\le300)\) ：https://codeforces.com/problemset/problem/213/C

题意：给定一个 n 行 n 列的网格图，问从左上走到右下，再从右下走到左上最多可以获得多少价值？一个单元格只能被计算一次价值。

注：弱化版中 -1 表示不可达，强化版没有不可达的约束。强化版 AC 代码

思路一：暴力dp

首先对于来回问题可以转化为两次去的问题，即问题等价于求解「两个人从左上角走到右下角」的最大收益。

显然我们可以定义四维的状态，其中 \(f[i][j][p][q]\) 表示第一个人走到 \((i,j)\) 且第二个人走到 \((p,q)\) 时的最大收益。直接枚举这四个维度，然后从 4 个合法的子问题转移过来即可。

时间复杂度：\(O(n^4)\)

思路二：优化dp

注意到问题可以进一步等价于「两个人同时从左上角走到右下角」的最大收益。也就是两个人到起点 \((0,0)\) 的曼哈顿距离应该是一样的，即 \(i+j=p+q\)，也就是说如果其中一个人 \((i,j)\) 的位置确定了，则另一个人只需要枚举一个下标，另一个下标就可以 \(O(1)\) 的确定了。可以将时间复杂度降低一个维度。

状态定义。我们定义 \(f[k][i_1][i_2]\) 表示第一个人走到 \((i_1,k-i_1)\) 且第二个人走到 \((i_2,k-i_2)\) 时的最大收益。则最终答案就是 \(f[2n-2][n-1][n-1]\)。状态转移同理，从 4 个合法子问题转移过来即可。

时间复杂度：\(O(n^3)\)

暴力dp：

template<class T>
void chmax(T& a, T b) {
    a = max(a, b);
}

int di[4] = {-1, -1, 0, 0};
int dj[4] = {0, 0, -1, -1};
int dp[4] = {-1, 0, -1, 0};
int dq[4] = {0, -1, 0, -1};

class Solution {
public:
    int cherryPickup(vector<vector<int>>& g) {
        int n = g.size();
        int f[n][n][n][n];
        memset(f, -1, sizeof f);
        f[0][0][0][0] = g[0][0] == -1 ? -1 : g[0][0];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (g[i][j] == -1) {
                    continue;
                }
                for (int p = 0; p < n; p++) {
                    for (int q = 0; q < n; q++) {
                        if (g[p][q] == -1) {
                            continue;
                        }
                        // 枚举 4 个子问题
                        for (int k = 0; k < 4; k++) {
                            int ni = i + di[k], nj = j + dj[k];
                            int np = p + dp[k], nq = q + dq[k];
                            if (ni >= 0 && nj >= 0 && np >= 0 && nq >= 0 && f[ni][nj][np][nq] != -1) {
                                chmax(f[i][j][p][q], f[ni][nj][np][nq] + g[i][j] + (i == p && j == q ? 0 : g[p][q]));
                            }
                        }
                    }
                }
            }
        }
        return f[n - 1][n - 1][n - 1][n - 1] == -1 ? 0 : f[n - 1][n - 1][n - 1][n - 1];
    }
};

优化dp：

template<class T>
void chmax(T& a, T b) {
    a = max(a, b);
}

int dx[] = {0, 0, -1, -1};
int dy[] = {0, -1, 0, -1};

class Solution {
public:
    int cherryPickup(vector<vector<int>>& g) {
        int n = g.size();
        int f[2 * n - 1][n][n];
        memset(f, -1, sizeof f);
        f[0][0][0] = g[0][0] == -1 ? -1 : g[0][0];
        for (int k = 1; k <= 2 * n - 2; k++) {
            for (int i1 = 0; i1 < n; i1++) {
                for (int i2 = 0; i2 < n; i2++) {
                    int j1 = k - i1, j2 = k - i2;
                    if (j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || g[i1][j1] == -1 || g[i2][j2] == -1) {
                        continue;
                    }
                    // 枚举 4 个子问题
                    for (int t = 0; t < 4; t++) {
                        int ni1 = i1 + dx[t], nj1 = k - ni1;
                        int ni2 = i2 + dy[t], nj2 = k - ni2;
                        if (ni1 >= 0 && nj1 >= 0 && ni2 >= 0 && nj2 >= 0 && f[k - 1][ni1][ni2] != -1) {
                            chmax(f[k][i1][i2], f[k - 1][ni1][ni2] + g[i1][j1] + (i1 == i2 && j1 == j2 ? 0 : g[i2][j2]));
                        }
                    }
                }
            }
        }
        return f[2 * n - 2][n - 1][n - 1] == -1 ? 0 : f[2 * n - 2][n - 1][n - 1];
    }
};

树形dp¶

最大社交深度和

https://vijos.org/d/nnu_contest/p/1534

算法：树形dp、BFS

题意：给定一棵树，现在需要选择其中的一个结点为根节点，使得深度和最大。深度的定义是以每个结点到树根所经历的结点数

思路一：暴力

显然可以直接遍历每一个结点，计算每个结点的深度和，然后取最大值即可

时间复杂度：\(O(n^2)\)

思路二：树形dp
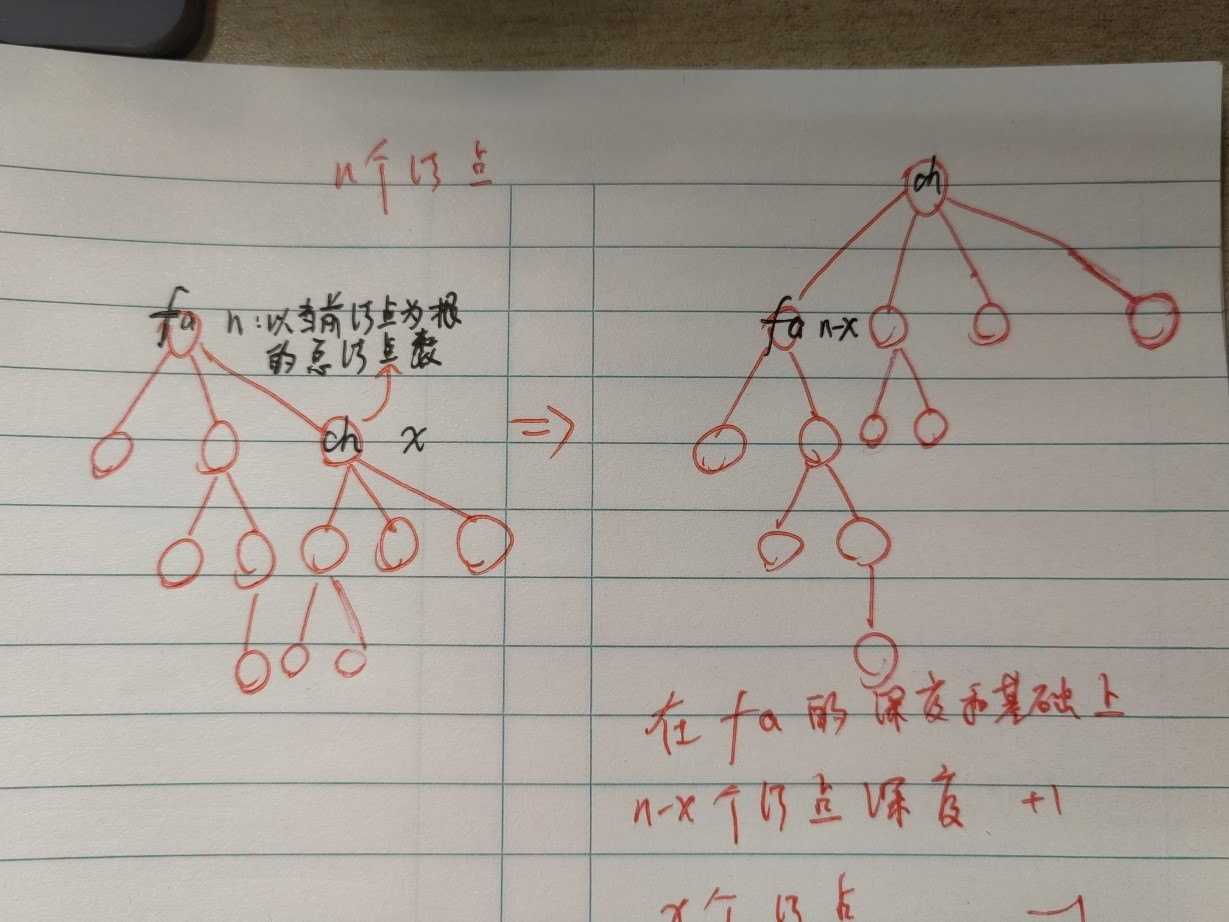
我们可以发现，对于当前的根结点 fa，我们选择其中的一个子结点 ch，将 ch 作为新的根结点（如右图）。那么对于当前的 ch 的深度和，我们可以借助 fa 的深度和进行求解。我们假设以 ch 为子树的结点总数为 x，那么这 x 个结点在换根之后，相对于 ch 的深度和，贡献了 -x 的深度；而对于 fa 的剩下来的 n-x 个结点，相对于 ch 的深度和，贡献了 n-x 的深度。于是 ch 的深度和就是 fa的深度和 -x+n-x，即：

\[ dep[ch] = dep[fa]-x+n-x = dep[fa]+n-2\times x \]

于是我们很快就能想到利用前后层的递推关系，\(O(1)\) 的计算出所有子结点的深度和。

代码实现：我们可以先计算出 base 的情况，即任选一个结点作为根结点，然后基于此进行迭代计算。在迭代计算的时候需要注意的点就是在一遍 dfs 计算某个结点的深度和 dep[root] 时，如果希望同时计算出每一个结点作为子树时，子树的结点数，显然需要分治计算一波。关于分治的计算我熟练度不够高，~~特此标注一下debug了3h的点~~：即在递归到最底层，进行回溯计算的时候，需要注意不能统计父结点的结点值（因为建的是双向图，所以一定会有从父结点回溯的情况），那么为了避开这个点，就需要在 \(O(1)\) 的时间复杂度内获得当前结点的父结点的编号，从而进行特判，采用的方式就是增加递归参数 fa。
没有考虑从父结点回溯的情况的dfs代码
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
void dfs(int now, int depth) {
    if (!st[now]) {
        st[now] = true;
        dep[root] += depth;
        for (auto& ch: G[now]) {
            dfs(ch, depth + 1);
            cnt[now] += cnt[ch];
        }
    }
}
考虑了从父结点回溯的情况的dfs代码
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
void dfs(int now, int fa, int depth) {
    if (!st[now]) {
        st[now] = true;
        dep[root] += depth;
        for (auto& ch: G[now]) {
            dfs(ch, now, depth + 1);
            if (ch != fa) {
                cnt[now] += cnt[ch];
            }
        }
    }
}
时间复杂度：\(\Theta(2n)\)

暴力代码：

const int N = 500010;

int n;
vector<int> G[N];
int st[N], dep[N];

void dfs(int id, int now, int depth) {
    if (!st[now]) {
        st[now] = 1;
        dep[id] += depth;
        for (auto& node: G[now]) {
            dfs(id, node, depth + 1);
        }
    }
}

void solve() {
    cin >> n;
    for (int i = 1; i <= n - 1; i++) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        G[b].push_back(a);
    }

    int res = 0;

    for (int i = 1; i <= n; i++) {
        memset(st, 0, sizeof st);
        dfs(i, i, 1);
        res = max(res, dep[i]);
    }

    cout << res << "\n";
}

优化代码：

const int N = 500010;

int n, dep[N], root = 1;
vector<int> G[N], cnt(N, 1);;
bool st[N];

// 当前结点编号 now，当前结点的父结点 fa，当前结点深度 depth
void dfs(int now, int fa, int depth) {
    if (!st[now]) {
        st[now] = true;
        dep[root] += depth;
        for (auto& ch: G[now]) {
            dfs(ch, now, depth + 1);
            if (ch != fa) {
                cnt[now] += cnt[ch];
            }
        }
    }
}

void bfs() {
    memset(st, 0, sizeof st);
    queue<int> q;
    q.push(root);
    st[root] = true;

    while (q.size()) {
        int fa = q.front(); // 父结点编号 fa
        q.pop();
        for (auto& ch: G[fa]) {
            if (!st[ch]) {
                st[ch] = true;
                dep[ch] = dep[fa] + n - 2 * cnt[ch];
                q.push(ch);
            }
        }
    }
}

void solve() {
    cin >> n;
    for (int i = 1; i <= n - 1; i++) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        G[b].push_back(a);
    }

    dfs(root, -1, 1);
    bfs();

    cout << *max_element(dep, dep + n + 1) << "\n";
}

高维dp¶

栈

https://www.luogu.com.cn/problem/P1044

题意：n个数依次进栈，随机出栈，问一共有多少种出栈序列？

思路一：dfs

我们可以这么构造搜索树：已知对于当前的栈，一共有两种状态

入栈 - 如果当前还有数没有入栈

出栈 - 如果当前栈内还有元素

搜索参数：i,j 表示入栈数为 i 出栈数为 j 的状态

搜索终止条件

入栈数 < 出栈数 - \(i<j\)

入栈数 > 总数 \(n\) - \(i = n\)

答案状态：入栈数为n，出栈数也为n

时间复杂度：\(O(\text{方案数})\)

思路二：dp

采用上述dfs时的状态表示方法，i,j 表示入栈数为 i 出栈数为 j 的状态。

我们在搜索的时候，考虑的是接下来可以搜索的状态

即出栈一个数的状态 - i+1,j

和入栈一个数的状态 - i,j+1

如图：

而我们在dp的时候，需要考虑的是子结构的解来得出当前状态的答案，就需要考虑之前的状态。即当前状态是从之前的哪些状态转移过来的。和上述dfs思路是相反的。我们需要考虑的是

上一个状态入栈一个数到当前状态 - i-1,j \(\to\) i,j

上一个状态出栈一个数到当前状态 - i,j-1 \(\to\) i,j

特例：\(i=j\) 时，只能是上述第二种状态转移而来，因为要始终保证入栈数大于等于出栈数，即 \(i \ge j\)

如图：

我们知道，入栈数一定是大于等于出栈数的，即 \(i\ge j\)。于是我们在枚举 \(j\) 的时候，枚举的范围是 \([1,i]\)

\(base\) 状态的构建取决于 \(j=0\) 时的所有状态，我们知道没有任何数出栈也是一种状态，于是

\[ dp[i][0]=0,(i=1,2,3,...,n) \]

时间复杂度：\(O(n^2)\)

dfs代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int n, res;

// 入栈i个数，出栈j个数
void dfs(int i, int j) {
    if (i < j || i > n) return;

    if (i == n && j == n) res++;

    dfs(i + 1, j);
    dfs(i, j + 1);
}

void solve() {
    cin >> n;
    dfs(0, 0);
    cout << res << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

dp代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 20;

int n;
ll dp[N][N]; // dp[i][j] 表示入栈数为i，出栈数为j的方案总数

void solve() {
    cin >> n;

    // base状态：没有数出栈也是一种状态
    for (int i = 1; i <= n; i++) dp[i][0] = 1;

    // dp转移
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= i; j++)
            if (i == j) dp[i][j] = dp[i][j - 1];
            else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

    cout << dp[n][n] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

找出所有稳定的二进制数组 II

https://leetcode.cn/problems/find-all-possible-stable-binary-arrays-ii/

题意：构造一个仅含有 \(n\) 个 \(0\)，\(m\) 个 \(1\) 的数组，且长度超过 \(k\) 的子数组必须同时含有 \(0\) 和 \(1\)。给出构造的总方案数对 \(10^9+7\) 取余后的结果。

思路：

定义状态表。我们从左到右确定每一位的数字时，需要确定这么三个信息：当前是哪一位？还剩几个 \(0\) 和 \(1\)？这一位填 \(0\) 还是 \(1\)？对于这三个信息，我们可以定义状态数组 \(f[i][j][k]\) 表示当前已经选了 \(i\) 个 \(0\)，\(j\) 个 \(1\)，且第 \(i+j\) 位填 \(k\) 时的方案数。这样最终答案就是 \(f[n][m][0]+f[n][m][1]\)。

定义子问题。以当前第 \(i+j\) 位填 \(0\) 为例，填 \(1\) 同理，即当前需要维护的是 \(f[i][j][0]\)。显然的如果前一位是和当前位不同，即 \(1\) 时，可以直接转移过来；如果前一位和当前位相同，即 \(0\) 时，有可能会出现长度超过 \(k\) 的连续 \(0\) 子数组，即前段数组刚好是以「一个 \(1\) 和 \(k\) 个 \(0\) 结尾的」合法数组，此时再拼接一个 \(0\) 就不合法了。

状态转移方程。综上所述，可以得到以下两个状态转移方程：

\[ \begin{aligned} f[i][j][0] = f[i - 1][j][1] + f[i - 1][j][0] - f[i - k - 1][j][1] \\ f[i][j][1] = f[i][j - 1][0] + f[i][j - 1][1] - f[i][j - k - 1][0] \end{aligned} \]

时间复杂度：\(O(nm)\)

class Solution {
public:
    int numberOfStableArrays(int n, int m, int k) {
        const int mod = 1e9 + 7;
        vector<vector<array<int, 2>>> f(n + 1, vector<array<int, 2>>(m + 1));

        for (int i = 0; i <= min(n, k); i++) {
            f[i][0][0] = 1;
        }
        for (int j = 0; j <= min(m, k); j++) {
            f[0][j][1] = 1;
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                f[i][j][0] = (f[i - 1][j][1] + f[i - 1][j][0]) % mod;
                if (i - k - 1 >= 0) {
                    f[i][j][0] = (f[i][j][0] - f[i - k - 1][j][1] + mod) % mod;
                }
                f[i][j][1] = (f[i][j - 1][0] + f[i][j - 1][1]) % mod;
                if (j - k - 1 >= 0) {
                    f[i][j][1] = (f[i][j][1] - f[i][j - k - 1][0] + mod) % mod;
                }
            }
        }

        return (f[n][m][0] + f[n][m][1]) % mod;
    }
};

学生出勤记录 II

https://leetcode.cn/problems/student-attendance-record-ii/description/

题意：构造一个仅含有 \(P,A,L\) 三种字符的字符串，使得 \(A\) 最多出现 \(1\) 次，同时 \(L\) 最多连续出现 \(2\) 次。问一共有多少种构造方案？对 \(10^9+7\) 取模。

思路：

模拟分析问题。我们从前往后构造。对于当前第 \(i\) 个字符 \(s[i]\)，有 \(3\) 种可能的选项，其中 \(P\) 是一定合法的选项，\(A\) 是否合法取决于 \(s[0:i-1]\) 中的 \(A\) 的数量，\(L\) 是否合法取决于 \(s[0:i-1]\) 的末尾连续 \(L\) 的数量。因此我们可以通过被动转移的动态规划求解。

状态定义。从上述分析不难发现需要 \(3\) 种状态来表示所有情况，因此我们定义 \(f[i][j][k]\) 表示构造第 \(i\) 位时，\(s[0:i]\) 中含有 \(j\) 个 \(A\) 且末尾含有连续 \(k\) 个 \(L\) 时的方案数。

初始化。每一位填什么取决于前缀 \(s[0:i-1]\) 的情况，因此我们需要初始化 \(f[0][][]\) 即第 \(0\) 位的情况。显然的第 \(0\) 位 \(P,A,L\) 三种都可以填，对应的就是 \(f[0][0][0] = f[0][1][0] = f[0][0][1] = 1\)，其余初始化为 \(0\) 即可。

状态转移。考虑第 \(i\) 位的三种情况：

填 \(P\)：可以用前缀的所有状态来更新 \(f[i][j][0]\)

填 \(A\)：可以用前缀中不含 \(A\) 的所有状态来更新 \(f[i][1][0]\)

填 \(L\)：可以用前缀中末尾不超过 \(1\) 位 \(L\) 的所有状态来更新 \(f[i][j][k]\)

最终答案。为 \(\displaystyle \sum_{j=0}^{1}\sum_{k=0}^{2}f[n-1][j][k]\)。

时间复杂度：\(\Theta (6n)\)

class Solution {
public:
    int checkRecord(int n) {
        const int mod = 1e9 + 7;

        // f[i][j][k]表示从左往右构造第i位时，s[0:i]中含有j个A且尾部含有连续k个L时的方案数
        int f[n][2][3];
        memset(f, 0, sizeof f);

        // 初始化
        f[0][0][0] = f[0][1][0] = f[0][0][1] = 1;

        // 转移
        for (int i = 1; i < n; i++) {
            // s[i]填P
            for (int j = 0; j <= 1; j++) {
                for (int k = 0; k <= 2; k++) {
                    f[i][j][0] = (f[i][j][0] + f[i - 1][j][k]) % mod;
                }
            }
            // s[i]填A
            for (int k = 0; k <= 2; k++) {
                f[i][1][0] = (f[i][1][0] + f[i - 1][0][k]) % mod;
            }
            // s[i]填L
            for (int j = 0; j <= 1; j++) {
                for (int k = 1; k <= 2; k++) {
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j][k - 1]) % mod;
                }
            }
        }

        // 计算答案
        int res = 0;
        for (int j = 0; j <= 1; j++) {
            for (int k = 0; k <= 2; k++) {
                res = (res + f[n - 1][j][k]) % mod;
            }
        }
        return res;
    }
};

class Solution:
    def checkRecord(self, n: int) -> int:
        mod = int(1e9 + 7)
        f = [[[0, 0, 0] for _ in range(2)] for _ in range(n)]
        f[0][0][0] = f[0][1][0] = f[0][0][1] = 1
        for i in range(1, n):
            # P
            for j in range(2):
                for k in range(3):
                    f[i][j][0] = (f[i][j][0] + f[i - 1][j][k]) % mod
            # A
            for k in range(3):
                f[i][1][0] = (f[i][1][0] + f[i - 1][0][k]) % mod
            # L
            for j in range(2):
                for k in range(1, 3):
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j][k - 1]) % mod
        res = 0
        for j in range(2):
            for k in range(3):
                res = (res + f[n - 1][j][k]) % mod
        return res

区间dp¶

对称山脉

https://www.acwing.com/problem/content/5169/

模拟，时间复杂度 \(O(n^3)\)

#include <iostream>
#include <cmath>

using namespace std;

const int N = 5010;

int n;
int a[N];

int main() {
    cin >> n;

    for (int i = 1; i <= n; i++)
        cin >> a[i];

    // 枚举区间长度
    for (int len = 1; len <= n; len++) {
        int res = 2e9;
        // 枚举相应长度的所有区间
        for (int i = 1, j = i + len - 1; j <= n; i++, j++) {
            // 计算区间的不对称值
            int l = i, r = j;
            int sum = 0;
            while (l < r) {
                sum += abs(a[l] - a[r]);
                l++, r--;
            }
            res = min(res, sum);
        }
        cout << res << ' ';
    }

    return 0;
}

dp优化，时间复杂度 \(O(n^2)\)

#include <iostream>
#include <cmath>
#include <cstring>

using namespace std;

const int N = 5010;

int n;
int a[N];

int dp[N][N]; // dp[i][j] 表示第 i 到 j 的不对称值
int res[N];   // res[len] 表示长度为 len 的山脉的最小不对称值 

int main() {
    cin >> n;

    for (int i = 1; i <= n; i++)
        cin >> a[i];

    memset(res, 0x3f, sizeof res);

    // 长度为 1 的情况
    res[1] = 0;

    // 长度为 2 的情况
    for (int i = 1, j = i + 1; j <= n; i++, j++) {
        dp[i][j] = abs(a[i] - a[j]);
        res[2] = min(res[2], dp[i][j]);
    }

    // 长度 >= 3 的情况 
    for (int len = 3; len <= n; len++) {
        for (int i = 1, j = i + len - 1; j <= n; i++, j++) {
            dp[i][j] = dp[i + 1][j - 1] + abs(a[i] - a[j]);
            res[len] = min(res[len], dp[i][j]);
        }
    }

    for (int i = 1; i <= n; i++)
        cout << res[i] << ' ';

    return 0;
}

状压dp¶

Avoid K Palindrome

https://atcoder.jp/contests/abc359/tasks/abc359_d

题意：给定一个长度为 \(n\le 1000\) 的字符串 \(s\) 和一个整数 \(k\le10\)，其中含有若干个 'A','B' 和 '?'。其中 '?' 可以转化为 'A' 或 'B'，假设有 \(q\) 和 '?'，则一共可以转化出 \(2^q\) 个不同的 \(s\)。问所有转化出的 \(s\) 中，有多少是不含有长度为 \(k\) 的回文子串的。

思路：最暴力的做法就是 2^q 枚举所有可能的字符串，然后再 O(n) 的检查，这样时间复杂度为 \(O(n2^n)\)，只能通过 20 以内的数据。一般字符串回文问题可以考虑 dp。

图论¶

图论的「例题解析」。

拓扑¶

有向图的拓扑序列

https://www.acwing.com/problem/content/850/

题意：输出一个图的拓扑序，不存在则输出-1

思路：

首先我们要知道拓扑图的概念，感官上就是一张图可以从一个方向拓展到全图，用数学语言就是：若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列

接着我们就想要寻找这样的序列 A 了，可以发现对于每一个可扩展的点，入度一定为0，那么我们就从这些点开始宽搜，将搜到的点的入度-1，即删除这条边，直到最后。如果全图的点的入度都变为了0，则此图可拓扑

时间复杂度：\(O(n+m)\)

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int n, m;
vector<int> G[N];

void solve() {
    // 建图 
    cin >> n >> m;
    vector<int> d(n + 1, 0);
    for (int i = 1; i <= m; i++) {
        int a, b;
        cin >> a >> b;
        d[b]++;
        G[a].push_back(b);
    }

    // 预处理宽搜起始点集
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (!d[i])
            q.push(i);

    // 宽搜处理
    vector<int> res;
    while (q.size()) {
        auto h = q.front();
        q.pop();
        res.push_back(h);

        for (auto& ch: G[h]) {
            d[ch]--;
            if (!d[ch]) q.push(ch);
        }
    }

    // 输出合法拓扑序
    if (res.size() == n) {
        for (auto& x: res) {
            cout << x << " ";
        }
    } else {
        cout << -1 << "\n";
    }
}

int main() {
    solve();
    return 0;
}

Mad City

https://codeforces.com/contest/1873/problem/H

标签：基环树、拓扑排序

题意：给定一个基环树，现在图上有两个点，分别叫做A，B。现在B想要逃脱A的抓捕，问对于给定的局面，B能否永远逃离A的抓捕

思路：思路很简单，我们只需要分B所在位置的两种情况讨论即可

B不在环上：此时我们记距离B最近的环上的那个点叫 \(tag\)，我们需要比较的是A到tag点的距离 \(d_A\) 和B到tag的距离 \(d_B\)，如果 \(d_B < d_A\)，则一定可以逃脱，否则一定不可以逃脱

B在环上：此时我们只需要判断当前的A点是否与B的位置重合即可，如果重合那就无法逃脱，反之B一定可以逃脱。

代码实现：

对于第一种情况，我们需要找到tag点以及计算A和B到tag点的距离，

时间复杂度：

#include <bits/stdc++.h>
using namespace std;

const int N = 200010;

int n, a, b;
vector<int> G[N];
int rd[N], tag, d[N];
bool del[N], vis[N];

void init() {
    for (int i = 1; i <= n; i++) {
        G[i].clear();        // 存无向图 
        rd[i] = 0;            // 统计每一个结点的入度 
        del[i] = false;        // 拓扑删点删边时使用 
        d[i] = 0;            // 图上所有点到 tag 点的距离 
        vis[i] = false;        // bfs计算距离时使用 
    }
}

void topu(int now) {
    if (rd[now] == 1) {
        rd[now]--;
        del[now] = true;
        for (auto& ch: G[now]) {
            if (del[ch]) continue;
            rd[ch]--;
            if (now == tag) {
                tag = ch;
            }
            topu(ch);
        }
    }
}

void bfs() {
    queue<int> q;
    q.push(tag);
    d[tag] = 0;

    while (q.size()) {
        auto now = q.front();
        vis[now] = true;
        q.pop();

        for (auto& ch: G[now]) {
            if (!vis[ch]) {
                d[ch] = d[now] + 1;
                q.push(ch);
                vis[ch] = true;
            }
        }
    }
}

void solve() {
    // 初始化
    cin >> n >> a >> b; 
    init();

    // 建图 
    for (int i = 1; i <= n; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v), rd[v]++;
        G[v].push_back(u), rd[u]++;
    }

    // 拓扑删边 & 缩b点
    tag = b;
    for (int i = 1; i <= n; i++) {
        topu(i);
    }

    // 判断结果 & 计算距离 
    if (rd[b] == 2 && a != b) {
        // b点在环上
        cout << "Yes\n";
    } else {
        // b不在环上
        bfs();
        cout << (d[a] > d[b] ? "Yes\n" : "No\n");
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T = 1;
    cin >> T;
    while (T--) solve();
    return 0;
}

二分图¶

染色法判定二分图

https://www.acwing.com/problem/content/862/

题意：给定一个无向图，可能有重边和自环。问是否可以构成二分图。

二分图的定义：一个图可以被分成两个点集，每个点集内部没有边相连（可以不是连通图）

思路：利用染色法，遍历每一个连通分量，选择连通分量中的任意一点进行染色扩展

如果扩展到的点没有染过色，则染成与当前点相对的颜色

如果扩展到的点已经被染过色了且染的颜色和当前点的颜色相同，则无法构成二分图（奇数环）

时间复杂度：\(O(n+e)\)

const int N = 100010;

int n, m;
vector<int> G[N], col(N);

bool bfs(int u) {
    queue<int> q;
    q.push(u);
    col[u] = 1;

    while (q.size()) {
        int now = q.front();
        q.pop();
        for (auto& ch: G[now]) {
            if (!col[ch]) {
                col[ch] = -col[now];
                q.push(ch);
            }
            else if (col[ch] == col[now]) {
                return false;
            }
        }
    }

    return true;
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }

    // 遍历每一个连通分量
    for (int i = 1; i <= n; i++) {
        if (!col[i]) {
            bool ok = bfs(i);
            if (!ok) {
                cout << "No\n";
                return;
            }
        }
    }

    cout << "Yes\n";
}

最小生成树¶

Kruskal算法求最小生成树

https://www.acwing.com/problem/content/861/

题意：给定一个无向图，可能含有重边和自环。试判断能否求解其中的最小生成树，如果可以给出最小生成树的权值

思路：根据数据量，可以发现顶点数很大，不适用 \(Prim\) 算法，只能用 \(Kruskal\) 算法，下面简单介绍一下该算法的流程

自环首先排除 - 显然这条边连接的“两个”顶点是不可能选进 \(MST\) 的

首先将每一个结点看成一个连通分量

接着按照权值将所有的边升序排序后，依次选择

如果选出的这条边的两个顶点不在一个连通分量中，则选择这条边并将两个顶点所在的连通分量合并

如果选出的这条边的两个顶点在同一个连通分量中，则不能选择这条边（否则会使得构造的树形成环）

最后统计选择的边的数量 \(num\) 进行判断即可

\(num=n-1\)，则可以生成最小生成树

\(num<n-1\)，则无法生成最小生成树

时间复杂度：\(O(e\log e)\) - 因为最大的时间开销在对所有的边的权值进行排序上

C++

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 100010;

struct edge {
    int a, b;
    int w;
};

int n, m;
vector<edge> edges;
vector<int> p(N);

int Find(int now) {
    if (p[now] != now) {
        p[now] = Find(p[now]);
    }
    return p[now];
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        if (a == b) {
            continue;
        }
        edges.push_back({a, b, w});
    }

    // 按照边权升序排序
    sort(edges.begin(), edges.end(), [&](edge& x, edge& y) {
        return x.w < y.w;
    });

    // 选边
    for (int i = 1; i <= n; i++) {
        p[i] = i;
    }

    int res = 0, num = 0;

    for (auto& e: edges) {
        int pa = Find(e.a), pb = Find(e.b);
        if (pa != pb) {
            num++;
            p[pa] = pb;
            res += e.w;
        }

        if (num == n - 1) {
            break;
        }
    }

    // 特判：选出来的边数无法构成一棵树
    if (num < n - 1) {
        cout << "impossible\n";
        return;
    }

    cout << res << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

Python

def Find(x: int, p: list) -> int:
    if p[x] != x: p[x] = Find(p[x], p)
    return p[x]

def kruskal(n: int, m: int, edges: list) -> int:
    # 按边权对边进行降序排序
    edges.sort(key=lambda edge: edge[-1])

    # dsu 初始化
    p = [None] + [i for i in range(1, n + 1)]

    # 选边
    cnt = sum = 0
    for edge in edges:
        if cnt == n - 1: break

        pa, pb = Find(edge[0], p), Find(edge[1], p)
        if pa != pb:
            p[pa] = pb
            cnt += 1
            sum += edge[2]

    return sum if cnt == n - 1 else 0


if __name__ == "__main__":
    n, m = map(int, input().split())

    edges = []
    for i in range(m):
        edge = tuple(map(int, input().split()))
        edges.append(edge)

    res = kruskal(n, m, edges)

    if res: print(res)
    else: print("impossible")

JavaScript

const readline = require('readline');
const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout,
});

let n = null;
let m = null;
const edges = [];

rl.on('line', line => {
    const [a, b, c] = line.split(' ').map(i => Number(i));
    if (n === null) {
        n = a;
        m = b;
    } else {
        edges.push([a, b, c]);
    }
});

rl.on('close', () => {
    const res = kurskal(n, m, edges);
    console.log(res === Infinity ? 'impossible' : res);
});

function Find(x, p) {
    if (p[x] != x) p[x] = Find(p[x], p);
    return p[x];
}

function kurskal(n, m, edges) {
    // 对边进行升序排序
    edges.sort((a, b) => a[2] - b[2]);

    // 初始化 dsu
    p = [];
    for (let i = 1; i <= n; i++) p[i] = i;

    // 选边
    let cnt = 0, sum = 0;
    for (let [a, b, w] of edges) {
        if (cnt == n - 1) {
            break;
        }

        let pa = Find(a, p), pb = Find(b, p);
        if (pa !== pb) {
            cnt++;
            p[pa] = pb;
            sum += w;
        }
    }

    if (cnt === n - 1) return sum;
    else return Infinity;
}

Prim算法求最小生成树

https://www.acwing.com/problem/content/860/

题意：给定一个稠密无向图，有重边和自环。求出最小生成树

思路：根据题目的数据量，可以使用邻接矩阵存储的方法配合 \(Prim\) 算法求解最小生成树，下面给出该算法的流程

首先明确一下变量的定义：

g[i][j] 为无向图的邻接矩阵存储结构

MST[i] 表示 \(i\) 号点是否加入了 \(MST\) 集合

d[i] 表示 i 号点到 \(MST\) 集合的最短边长度

自环不存储，重边只保留最短的一条

任选一个点到集合 \(MST\) 中，并且更新 \(d\) 数组

选择剩余的 \(n-1\) 个点，每次选择有以下流程

找到最短边，记录最短边长度 \(e\) 和相应的在 \(U-MST\) 集合中对应的顶点序号 \(v\)

将 \(v\) 号点加入 \(MST\) 集合，同时根据此时选出的最短边的长度来判断是否存在最小生成树

根据 \(v\) 号点，更新 \(d\) 数组，即更新在集合 \(U-MST\) 中的点到 \(MST\) 集合中的点的交叉边的最短长度

时间复杂度：\(O(n^2)\)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 510;

int n, m;
vector<vector<int>> g(N, vector<int>(N, INT_MAX));
vector<int> d(N, INT_MAX); // d[i]表示i号点到MST集合中的最短边长度
bool MST[N];
int res;

void prim() {
    // 选任意一个点到MST中并更新d数组
    MST[1] = true;
    for (int i = 1; i <= n; i++)
        if (!MST[i])
            d[i] = min(d[i], g[i][1]);

    // 选剩下的n-1个点到MST中
    for (int i = 2; i <= n; i++) {
        // 1. 找到最短边
        int e = INT_MAX, v = -1; // e: 最短边长度，v: 最短边不在MST集合中的顶点
        for (int j = 1; j <= n; j++)
            if (!MST[j] && d[j] < e)
                e = d[j], v = j;

        // 2. 加入MST集合
        MST[v] = true;
        if (e == INT_MAX) {
            // 特判无法构造MST的情况
            cout << "impossible\n";
            return;
        } else {
            res += e;
        }

        // 3. 更新交叉边 - 迭代（覆盖更新）
        for (int j = 1; j <= n; j++)
            if (!MST[j])
                d[j] = min(d[j], g[j][v]);
    }

    cout << res << "\n";
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;

        if (a == b) {
            continue;
        }

        if (g[a][b] == INT_MAX) {
            g[a][b] = w;
            g[b][a] = w;
        } else {
            g[a][b] = min(g[a][b], w);
            g[b][a] = min(g[b][a], w);
        }
    }

    prim();
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

最短路¶

Dijkstra求最短路

朴素版 - https://www.acwing.com/problem/content/851/

堆优化 - https://www.acwing.com/problem/content/852/

题意：给定一个正边权的有向图，可能存在重边与自环，问 \(1\) 号点到 \(n\) 号点的最短路径长度是多少，如果不可达就输出 \(-1\)。

思路一：朴素版。点数 \(1\le n \le 500\)，边数 \(1 \le m\le 10^5\)

思路：根据数据量，我们采用邻接矩阵的方式存储「点少边多」的稠密图。我们定义 d[i] 数组表示起点到 i 号点的最短距离。先将起点放入 SPT (Shortest Path Tree) 集合，然后更新所有 V-SPT 中的点到 SPT 集合的最短路径长度。接着循环 n-1 次迭代更新剩余的 n-1 个点，每次迭代的过程中，首先选择距离起点最近的点 vex，然后将该点加入 SPT 集合，最后利用该点更新 V-SPT 集合中和该点有连边的点到起点的最短距离。最终的 d[end] 就是起点 start 到终点 end 的最短距离。

总结：算法整体采用贪心与动态规划的思路。与 \(\text{Prim}\) 算法仔细比对可知，其中的贪心过程几乎一致，即每次选择加入 SPT 集合的点均为当前局面 V-SPT 集合中距离起点最近的点。而动态规划的过程体现在，在求解出集合 V-SPT 中到集合 STP 最短距离的点 vex 之后，利用该点对「在 V-SPT 集合且和 vex 点有连边的点 i」更新 d[i] 的过程。更新前的状态都是在之前的子结构下的最优解。

时间复杂度：\(O(n^2)\)

思路二：堆优化。点数 \(1\le n \le 1.5 \times 10^5\)，边数 \(1 \le m \le 1.5 \times 10^5\)

思路：根据数据量，我们采用邻接表的方式存储「点多边少」的稀疏图。如果采用上述朴素 Dijkstra 算法进行求解必然会因为点数过多而超时，因此我们利用数据结构「堆」进行时间开销上的优化。不难发现朴素 Dijkstra 算法在迭代过程中主要有三部分：

选择距离起点最近的点 vex。因为需要枚举所有的顶点，因此总的时间复杂度为 \(O(n^2)\)

将该点加入 SPT 集合。因为只是简单的打个标记，因此总的时间复杂度为 \(O(n)\)

利用该点更新 V-SPT 集合中和该点相连的点到起点的最短距离。因为此时枚举的是该点所有的连边，而邻接表的图存储方式无法进行重边的删除，因此最坏情况下会枚举所有的边，时间复杂度为 \(O(m)\)

时间复杂度：

朴素版C++：

#include <bits/stdc++.h>

using ll = long long;
using namespace std;

int dijkstra_ori(std::vector<std::vector<int>>& g, int start, int end) {
    int n = g.size() - 1;
    std::vector<int> d(n + 1, INT_MAX >> 1);
    std::vector<bool> SPT(n + 1, false);

    // update start vex
    d[start] = 0;
    SPT[start] = true;
    for (int i = 1; i <= n; i++) {
        if (!SPT[i] && g[start][i] != INT_MAX >> 1) {
            d[i] = std::min(d[i], d[start] + g[start][i]);
        }
    }

    // update remain n-1 vex
    for (int k = 0; k < n - 1; k++) {
        int vex = -1;
        for (int i = 1; i <= n; i++) {
            if (!SPT[i] && (vex == -1 || d[i] < d[vex])) {
                vex = i;
            }
        }
        SPT[vex] = true;
        for (int i = 1; i <= n; i++) {
            if (!SPT[i] && g[vex][i] != INT_MAX >> 1) {
                d[i] = std::min(d[i], d[vex] + g[vex][i]);
            }
        }
    }

    return d[end] == INT_MAX >> 1 ? -1 : d[end];
}

void solve() {
    int n, m;
    cin >> n >> m;

    vector<vector<int>> g(n + 1, vector<int>(n + 1, INT_MAX >> 1));

    while (m--) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u][v] = min(g[u][v], w);
    }

    cout << dijkstra_ori(g, 1, n) << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
//    std::cin >> T;
    while (T--) solve();
    return 0;
}

朴素版Python：

import heapq
from collections import defaultdict
from typing import List, Tuple
import math
from itertools import combinations

II = lambda: int(input())
FI = lambda: float(input())
MII = lambda: tuple(map(int, input().split()))
LII = lambda: list(map(int, input().split()))


def dijkstra_ori(g: List[List[int]], start: int, end: int) -> int:
    n = len(g) - 1
    d = [10 ** 5] * (n + 1)
    SPT = [False] * (n + 1)

    d[start] = 0
    SPT[start] = True
    for i in range(1, n + 1):
        if not SPT[i] and g[start][i] != 10 ** 5:
            d[i] = min(d[i], d[start] + g[start][i])

    for _ in range(n - 1):
        vex = -1
        for i in range(1, n + 1):
            if not SPT[i] and (vex == -1 or d[i] < d[vex]):
                vex = i
        SPT[vex] = True
        for i in range(1, n + 1):
            if not SPT[i] and g[vex][i] != 10 ** 5:
                d[i] = min(d[i], d[vex] + g[vex][i])

    return -1 if d[end] == 10 ** 5 else d[end]


def solve() -> None:
    n, m = MII()
    g = [[10 ** 5] * (n + 1) for _ in range(n + 1)]
    for _ in range(m):
        u, v, w = MII()
        g[u][v] = min(g[u][v], w)
    print(dijkstra_ori(g, 1, n))


if __name__ == '__main__':
    T = 1
    # T = II()
    while T: solve(); T -= 1

堆优化版C++：

堆优化版Python：

Floyd求最短路

https://www.acwing.com/problem/content/856/

题意：给定一个稠密有向图，可能存在重边与自环，给出多个询问，需要给出每一个询问的两个点之前的最短路径长度

思路：我们采用动态规划的思路。在此使用多阶段决策的方法，即每一个路径状态为选择 \(1\to k\) 个点的情况下的最短路径长度

状态表示：f[k][i][j] 表示在前 \(k\) 个顶点中进行选择（中转），\(i\) 号点到 \(j\) 号点的最短路径长度

状态转移：对于第 \(k\) 个顶点，我们可以选择中转，也可以不中转。

对于不选择中转的情况：f[k][i][j] = f[k-1][i][j]

对于可选择中转的情况：f[k][i][j] = f[k-1][i][k] + f[k-1][k][j]

在其中取最小值即可，但是有一个注意点：对于第二种情况，选择是有一个约束的：即如果选择了 \(k\) 号点进行转移的话，那么 \(i\) 号点到 \(k\) 号点以及 \(k\) 号点到 \(j\) 号点都是需要有路径可达的，从而可以选择最小距离

初始化：即选择 0 个站点进行中转时，即 f[0][i][j] 的情况中，

如果 \(i\) 号点与 \(j\) 号点自环，则取 \(0\)

如果 \(i\) 号点与 \(j\) 号点之间有边，则取重边的最小值

如果 \(i\) 号点与 \(j\) 号点之间无边，则初始化为正无穷

答案状态：对于 \(a\) 号点到 \(b\) 号点之间的最小路径长度，就是 f[n][a][b]

时间复杂度：\(O(n^3)\)

空间复杂度：\(O(n^3)\)

空间优化推导：我们尝试优化掉记忆数组的第一维度

对于不选择的情况：由于决策局面 \(k\) 是从前往后枚举，故当前状态 f[k][i][j] 可以直接依赖于已经更新出来且不会被当前状态之后的状态再次覆盖的最优子结构 f[i][j]。即上一个局面的选择情况，就是不选择第 \(k\) 个顶点的情况

对于选择的情况：如果删除第一维度，我们担心的是当前状态 f[k][i][j] 依赖的两个状态 f[i][k] 与 f[k][j] 会不会被后续覆盖掉，即我们不确定 f[i][k] 与 f[k][j] 是否是当前第 k 个局面的最优子结构。尝试推导：

为了确定 f[i][k] 与 f[k][j] 是否是当前第 \(k\) 个局面的最优子结构，其实就是确定对于当前第 \(k\) 个局面，这两个状态会不会在当前状态 f[i][j] 之后被更新覆盖，那么我们就看这两个状态是从哪里转移过来进行更新的。如果 f[i][k] 与 f[k][j] 这两个状态的转移会依赖于当前状态之后的状态，那么删除第一维度就是错误的，反之就是成立的。

尝试推导 f[i][k] 与 f[k][j] 从何转移更新：利用我们未删除维度时正确的状态转移方程进行推演

我们知道：f[k][i][k] = min(f[k-1][i][k], f[k-1][i][k] + f[k-1][k][k])，其中的 f[k-1][k][k] 就是一个自环的路径长度，由于 \(floyd\) 算法的约束条件是没有负环，因此 f[k-1][k][k] 一定大于零，故 f[k][i][k] 一定取前者，即 f[k][i][k] = f[k-1][i][k]

同理可知：

f[k][k][j] = f[k-1][k][j]

基于上述推导我们可以知道，当前第 \(k\) 个决策局面中的 f[k][i][k] 与 f[k][k][j] 是依赖于上一个决策局面 \(k-1\) 的，也就是说这两个状态一定是早于当前状态 f[i][j] 被更新覆盖的，故 f[i][k] 与 f[k][j] 就是当前第 \(k\) 个局面的最优子结构，证毕，可以进行维度的删除

时间复杂度：\(O(n^3)\)

空间复杂度：\(O(n^2)\)

不优化空间

#include <bits/stdc++.h>
using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, Q;
int f[N][N][N];

int main() {
    cin >> n >> m >> Q;

    // init
    memset(f, INF, sizeof f);

    // add edges and generate base
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;
        if (a == b) continue;                           // 重边就不赋值
        else if (f[0][a][b] == INF) f[0][a][b] = w;     // 第一次加边则直接赋值
        else f[0][a][b] = min(f[0][a][b], w);           // 再次赋边权就取最小值
    }

    // generate base again
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) 
                f[0][i][j] = 0;                         // 自环取边权为 0

    // dp 
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++) {
                // 不选第k个顶点
                f[k][i][j] = f[k - 1][i][j];

                // 选择第k个顶点
                if (f[k - 1][i][k] != INF && f[k - 1][k][j] != INF)
                    f[k][i][j] = min(f[k][i][j], f[k - 1][i][k] + f[k - 1][k][j]);
            }

    // query
    while (Q--) {
        int a, b;
        cin >> a >> b;
        if (f[n][a][b] == INF) cout << "impossible\n";
        else cout << f[n][a][b] << "\n";
    }

    return 0;
}

优化空间

#include <bits/stdc++.h>
using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, Q;
int f[N][N];

int main() {
    cin >> n >> m >> Q;

    // init
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) f[i][j] = 0;
            else f[i][j] = INF;

    // base
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;
        if (a == b) continue;
        else if (f[a][b] == INF) f[a][b] = w;
        else f[a][b] = min(f[a][b], w);
    }

    // dp
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (f[i][k] != INF && f[k][j] != INF)
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j]);

    // query
    while (Q--) {
        int a, b;
        cin >> a >> b;
        if (f[a][b] == INF) cout << "impossible\n";
        else cout << f[a][b] << "\n";
    }

    return 0;
}

关闭分部的可行集合数目

https://leetcode.cn/problems/number-of-possible-sets-of-closing-branches/

标签：二进制枚举、最短路

题意：给定一个含有 \(n\) 个顶点的无向图，如何删点可以使得剩余的图中顶点两两可达且最大距离不超过 maxDistance？返回所有删点的方案数。

思路：由于 \(n\) 的数据范围只有 \(1 \to 10\)，我们可以直接枚举所有的删点方案。那么如何检查一个方案的合法性呢？直接使用最短路算法检查「所有顶点到每一个顶点」的最远距离即可。这里我们采用朴素 dijkstra 算法。

时间复杂度：\(O(2^n \times n^3)\) - 其中枚举需要 \(O(2^n)\)、计算所有顶点到某个顶点的最远距离需要 \(O(n^2)\)、检查所有顶点需要 \(O(n)\)

class Solution {
public:
    int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
        vector<vector<int>> g(n, vector<int>(n, INT_MAX >> 1));
        for (auto& r: roads) {
            int u = r[0], v = r[1], w = r[2];
            g[u][v] = g[v][u] = min(g[u][v], w);
        }

        auto get_max_dist = [&](int mask, int v) {
            vector<bool> SPT(n);
            vector<int> d(n, INT_MAX);

            d[v] = 0;
            SPT[v] = true;

            int cnt = 0;
            for (int i = 0; i < n; i++) {
                if (mask & (1 << i) && !SPT[i]) {
                    cnt++;
                    d[i] = min(d[i], d[v] + g[v][i]);
                }
            }

            for (int k = 1; k <= cnt - 1; k++) {
                int vex = -1;
                for (int i = 0; i < n; i++) {
                    if (mask & (1 << i) && !SPT[i] && (vex == -1 || d[i] < d[vex])) {
                        vex = i;
                    }
                }
                SPT[vex] = true;
                for (int i = 0; i < n; i++) {
                    if (mask & (1 << i) && !SPT[i]) {
                        d[i] = min(d[i], d[vex] + g[vex][i]);
                    }
                }
            }

            int max_dist = -1;
            for (int i = 0; i < n; i++) {
                if (mask & (1 << i)) {
                    max_dist = max(max_dist, d[i]);
                }
            }

            return max_dist;
        };

        int res = 0;
        for (int mask = 0; mask < 1 << n; mask++) {
            bool ok = true;
            for (int i = 0; i < n; i++) {
                if (mask & (1 << i) && get_max_dist(mask, i) > maxDistance) {
                    ok = false;
                    break;
                }
            }
            res += ok;
        }

        return res;
    }
};

class Solution:
    def numberOfSets(self, n: int, maxDistance: int, roads: List[List[int]]) -> int:
        g = [[10 ** 6 for _ in range(n)] for _ in range(n)]
        for u, v, w in roads:
            g[u][v] = g[v][u] = min(g[u][v], w)

        def get_max_dist(mask: int, v: int):
            SPT = [False for _ in range(n)]
            d = [10 ** 6 for _ in range(n)]

            SPT[v] = True
            d[v] = 0

            cnt = 0
            for i in range(n):
                if mask & (1 << i) and not SPT[i]:
                    cnt += 1
                    d[i] = min(d[i], d[v] + g[v][i])

            for _ in range(cnt - 1):
                vex = -1
                for i in range(n):
                    if mask & (1 << i) and not SPT[i] and (vex == -1 or d[i] < d[vex]):
                        vex = i
                SPT[vex] = True
                for i in range(n):
                    if mask & (1 << i) and not SPT[i]:
                        d[i] = min(d[i], d[vex] + g[vex][i])

            max_dist = -1
            for i in range(n):
                if mask & (1 << i):
                    max_dist = max(max_dist, d[i])

            return max_dist

        res = 0
        for mask in range(1 << n):
            ok = True
            for i in range(n):
                if mask & (1 << i) and get_max_dist(mask, i) > maxDistance:
                    ok = False
                    break
            res += ok

        return res

博弈论¶

博弈论的「例题解析」。思考如何必胜态和必败态是什么以及如何构造这样的局面。

Salyg1n and the MEX Game

https://codeforces.com/contest/1867/problem/C

标签：博弈、贪心、交互

题面：对于给定n个数的数列，先手可以放入一个数列中不存在的数（0-1e9），后手可以从数列中拿掉一个数，但是这个数必须严格小于刚才先手放入的数。终止条件：后手没法拿数或者操作次数达到了 2n+1 次。问：当你是先手时，如何放数可以使得最终数列的 MEX 值最大。

思路：先手每次放入的数一定是当前数列的 MEX 值，此后不管后手拿掉什么数，先手都将刚刚被拿掉的数放进去即可。那么最多操作次数就刚好是 2n+1次，因为加入当前数列就是一个从 0 开始的连续整数数列，那么先手放入的数就是最大数 +1，即 n，那么假如后手从 n-1 开始拿，后手最多拿 n 次，先手再放 n 次，那么就是 2n+1 次。

时间复杂度：\(O(n)\)

#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int T; cin >> T;

    while (T--)
    {
        int n; cin >> n;
        vector<int> a(n);

        for (int i = 0; i < n; i ++)
            cin >> a[i];

        int mex = n;
        for (int i = 0; i < n; i ++)
            if (a[i] != i)
            {
                mex = i;
                break;
            }

        cout << mex << endl;

        int remove;
        cin >> remove;

        while (remove != -1)
        {
            cout << remove << endl;
            cin >> remove;
        }
    }

    return 0;
} 

计算几何¶

计算几何的「例题解析」。

Minimum Manhattan Distance

https://codeforces.com/gym/104639/problem/J

标签：二维、数学

题意：给定两个圆的直径的两个点坐标，其中约束条件是两个圆一定是处在相离的两个角上。问如何在C2圆上或圆内找到一点p，使得点p到C1圆的所有点的曼哈顿距离的期望值最小

思路：

看似需要积分，其实我们可以发现，对于点p到C1中某个点q1的曼哈顿距离，我们一定可以找到q1关于C1对称的点q2，那么点p到q1和q2的曼哈顿距离之和就是点p到C1的曼哈顿距离的两倍（证明就是中线定理）那么期望的最小值就是点p到C1的曼哈顿距离的最小值。目标转化后，我们开始思考如何计算此目标的最小值，思路如下图

注意点：

double的读取速度很慢，可以用 int or long long 读入，后续强制类型转换（显示 or 和浮点数计算）

注意输出答案的精度控制 cout << fixed << setprecision(10) << res << "\n";

void solve() {
    double x1, y1, x2, y2;
    long long a, b, c, d;

    cin >> a >> b >> c >> d;
    x1 = (a + c) / 2.0;
    y1 = (b + d) / 2.0;

    cin >> a >> b >> c >> d;
    x2 = (a + c) / 2.0;
    y2 = (b + d) / 2.0;

    double r2 = sqrt((a - c) * (a - c) + (b - d) * (b - d)) / 2;

    cout << fixed << setprecision(10) <<  abs(x1 - x2) + abs(y1 - y2) - sqrt(2) * r2 << "\n";
}

三角形

https://www.acwing.com/problem/content/5383/

标签：枚举

题意：给定两个直角三角形的两条直角边的长度 a, b，问能不能在坐标轴上找到三个整数点使得三点满足该直角三角形且三遍均不与坐标轴垂直

思路：首先确定两个直角边的顶点为原点 (0, 0)，接着根据对称性直接在第一象限中按照边长枚举其中一个顶点 A，对于每一个枚举到的顶点 A，按照斜率枚举最后一个顶点 B，如果满足长度以及不平行于坐标轴的条件就是合法的点。如果全部枚举完都没有找到就是没有合法组合，直接输出 NO 即可。

时间复杂度：\(O(a^2b)\)

#include <bits/stdc++.h>
using namespace std;

#define int long long

int a, b;

void solve() {
    cin >> a >> b;

    for (int i = 0; i <= a; i++) {
        for (int j = 0; j <= a; j++) {
            if (i * i + j * j == a * a && i && j) {
                int gcd = __gcd(i, j);
                int p = -i / gcd, q = j / gcd;
                int y = p, x = q;
                while (x * x + y * y < b * b) {
                    x += q, y += p;
                }
                if (x * x + y * y == b * b && x != i && y != j) {
                    cout << "YES\n";
                    cout << 0 << ' ' << 0 << "\n";
                    cout << i << ' ' << j << "\n";
                    cout << x << ' ' << y << "\n";
                    return;
                }
            }
        }
    }

    cout << "NO\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//  cin >> T;
    while (T--) solve();
    return 0;
}

奶牛过马路

https://www.acwing.com/problem/content/5572/

标签：凸包

题意：给定一个二维坐标系，现在有两个东西可以进行平移。

一个是起始位于 \((0,0)\) 的奶牛，可以沿着 \(y\) 轴以 \([0,u]\) 的速度正向或负向移动

一个是起始位于第一象限的凸包形状的车辆，可以向 \(x\) 轴负半轴以恒定的速度 \(v\) 移动

在给定凸包的 \(n\) 个顶点的情况下，以及不允许奶牛被车辆撞到的情况下，奶牛前进到 \((0,w)\) 的最短时间

思路：由于是凸包，因此每一个顶点同时满足的性质，就可以代表整个凸包满足的性质。那么对于奶牛和凸包，就一共有三个局面：

奶牛速度足够快。可以使得对于任意一个顶点 \((x,y)\) 在到达 y 轴时，都小于此时奶牛的 y 值，用时间来表示就是 \(\frac{y}{u} \le \frac{x}{v}\)，即 \(y \le \frac{u}{v}x\)，表示凸包上所有的顶点都在直线 \(y=\frac{u}{v}\) 的下方

凸包速度足够快。可以使得对于任意一个顶点 \((x,y)\) 在到达 y 轴时，都大于此时奶牛的 y 值，用时间来表示就是 \(\frac{y}{u} \ge \frac{x}{v}\)，即 \(y \ge \frac{u}{v}x\)，表示凸包上所有的顶点都在直线 \(y=\frac{u}{v}\) 的上方

上述两种都不满足，即直线 \(y=\frac{u}{v}\) 与凸包相交。此时奶牛就不能一直全速（u）前进到终点了，需要进行一定的减速 or 返回操作。有一个显然的结论就是，对于减速 or 返回的操作，都可以等价于后退一段距离后再全速（u）前进，因此对于需要减速 or 返回的操作，我们只需要计算出当前状态下应该后退的距离即可。再简洁的，我们就是需要平移直线 \(y=\frac{u}{v}\)，显然只能向下平移而非向上平移，因此其实就是计算出直线 \(y=\frac{u}{v}+b\) 的截距 \(b\) 使得最终的直线 \(y=\frac{u}{v}+b\) 满足第二种条件即可。那么如何计算这个 b 呢？很显然我们可以遍历每一个顶点取满足所有顶点都在直线 \(y=\frac{u}{v}+b\) 上方的最大截距 b 即可。

注意点：

浮点数比较注意精度误差，尽可能将除法转化为乘法

在比较相等时可以引入一个无穷小量 \(\epsilon=10^{-7}\)

注意答案输出精度要求，\(10^{-6}\) 就需要我们出至少 \(7\) 位小数

时间复杂度：\(O(n)\)

C++

#include <iostream>
#include <cstring>
#include <algorithm>
#include <iomanip>
using namespace std;
using ll = long long;

int main() {
    double n, w, v, u;
    cin >> n >> w >> v >> u;

    bool up = false, down = false;
    double b = 0;

    while (n--) {
        double x, y;
        cin >> x >> y;

        // 除法无法通过
        // if (y / x < u / v) down = true;
        // else if (y / x > u / v) up = true;

        // 转化为乘法以后才能通过
        if (y < u / v * x) down = true;
        else if (y > u / v * x) up = true;

        b = min(b, y - u / v * x);
    }

    if (up && down) cout << setprecision(7) << (w - b) / u;
    else cout << setprecision(7) << w / u;

    return 0;
}

Py

read = lambda: map(int, input().split())

n, w, v, u = read()
k = u / v
b = 0
up = False
down = False

for _ in range(n):
    x, y = read()
    if (y < k * x): down = True
    if (y > k * x): up = True
    b = min(b, y - k * x)

if (up and down): print((w - b) / u)
else: print(w / u)

数论¶

数论的「例题解析」。整数问题。

质数¶

Divide and Equalize

题意：给定 \(n\) 个数，问能否找到一个数 \(num\)，使得 \(num^n = \prod_{i=1}^{n}a_i\)

原始思路：起初我的思路是二分，我们需要寻找一个数使得n个数相乘为原数组所有元素之积，那么我们预计算出所有数之积，并且在数组最大值和最小值之间进行二分，每次二分出来的数计算n次方进行笔比较即可。但是有一个很大的问题是，数据量是 \(10^4\)，而数字最大为 \(10^6\)，最大之积为 \(10^{10}\) 吗？不是！最大之和才是，最大之积是 \(10^{6\times10^4}\)

最终思路：我们可以将选数看做多个水池匀水的过程。现在每一个水池的水高都不定，很显然我们一定可以一个值使得所有的水池的高度一致，即 \(\frac{\sum_{i=1}^{n}a_i}{n}\)。但是我们最终的数字是一个整数，显然不可以直接求和然后除以n，那么应该如何分配呢？我们知道水池之所以可以直接除以n，是因为水的最小分配单位是无穷小，可以随意分割；而对于整数而言，最小分配单位是什么呢？答案是质因子！为了通过分配最小单位使得最终的“水池高度一致”，我们需要让每一个“水池”获得的数值相同的质因子数量相同。于是我们只需要统计一下数组中所有数的质因子数量即可。如果对于每一种质因子的数量都可以均匀分配每一个数（即数量是n的整数倍），那么就一定可以找到这个数使得 \(num^n = \prod_{i=1}^{n}a_i\)

void solve() {
    int n;
    cin >> n;

    // 统计所有数字的所有质因数
    unordered_map<int, int> m;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;

        for (int k = 2; k <= x / k; k++) {
            if (x % k == 0) {
                while (x % k == 0) {
                    m[k]++;
                    x /= k;
                }
            }
        }

        if (x > 1) {
            m[x]++;
        }
    }

    // 查看每一种质因数是否是n的整数倍
    for (auto& x: m) {
        if (x.second % n) {
            cout << "No\n";
            return;
        }
    }

    cout << "Yes\n";
}

整除¶

Deja Vu

https://codeforces.com/contest/1891/problem/B

题意：给点序列 a 和 b，对于 b 中的每一个元素 \(b_i\)，如果 a 中的元素 \(a_j\) 能够整除 \(2^{b_i}\)，则将 \(a_j\) 加上 \(2^{b_i - 1}\)。给出最后的 a 序列

思路一：暴力枚举。

我们很容易就想到暴力的做法，即两层循环，第一层枚举 b 中的元素，第二层枚举 a 中的元素，如果 a 中的元素能够整除 2 的 \(b^i\) 次方，就将 a 中相应的元素加上一个值即可。但是时间复杂度肯定过不了，考虑优化。

时间复杂度：\(O(nm)\)

思路二：整除优化。

现在我们假设a中有一个数 \(a_j\) 是 \(2^{b_i}\) 的整数倍（其中 \(b_i\) 是b序列中第一个枚举到的能够让 \(a_i\) 整除的数），那么就有 \(a_j = k2^{b_i}(k=1,2,...,)\)，那么 \(a_j\) 就要加上 \(2^{b_i-1}\)，于是 \(a_j\) 就变为了 \(k2^{b_i}+2^{b_i-1}=(2k+1)2^{b_i-1}\)。此后 \(a_j\) 就一定是 \(2^t(t\in \left[ 1,b_i-1 \right])\) 的倍数。因此我们需要做的就是首先找到b序列中第一个数x，能够在a中找到数是 \(2^x\) 的整数倍。这一步可以这样进行：对于 a中的每一个数，我们进行30次循环统计当前数是否是 \(2^i\) 的倍数，如果是就用哈希表记录当前的 \(i\)。最后我们在遍历寻找 x 时，只需要查看当前的 x 是否被哈希过即可。接着我们统计b序列中从x开始的严格降序序列c（由题意知，次序列的数量一定 \(\le\) 30，因为b序列中数值的值域为 \([1~30]\)）。最后我们再按照原来的思路，双重循环 a 序列和 c 序列即可。

时间复杂度：\(O(30n)\)

void solve() {
    int n, m;
    cin >> n >> m;

    vector<int> a(n + 1), b(m + 1);
    unordered_map<int, int> ha;

    // 边读边哈希
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        for (int j = 30; j >= 1; j--) {
            if (a[i] % (1 << j) == 0) {
                ha[j]++;
            }
        }
    }

    for (int i = 1; i <= m; i++) {
        cin >> b[i];
    }

    // 寻找b中第一个能够让a[j]整除的数b[flag]
    int flag = -1;
    for (int i = 1; i <= m; i++) {
        if (ha[b[i]]) {
            flag = i;
            break;
        }
    }

    // 特判
    if (flag == -1) {
        for (int j = 1; j <= n; j++) {
            cout << a[j] << " \n"[j == n];
        }
        return;
    }

    // 寻找b中从flag开始的严格单调递减的序列c
    vector<int> c;
    c.push_back(b[flag]);
    for (; flag <= m; flag++) {
        if (b[flag] < c.back()) {
            c.push_back(b[flag]);
        }
    }

    // 暴力循环一遍即可
    for (int j = 1; j <= n; j++) {
        for (int k = 0; k < c.size(); k++) {
            if (a[j] % (1 << c[k]) == 0) {
                a[j] += 1 << (c[k] - 1);
            }
        }
    }

    for (int j = 1; j <= n; j++) {
        cout << a[j] << " \n"[j == n];
    }
}

组合数学¶

序列数量

https://www.acwing.com/problem/content/5571/

题意：给定 \(i(i=1,2,\cdots,n)\) 个苹果，将其分给 \(m\) 个人，问一共有多少种分配方案，给出结果对 \(10^6+3\) 取模的结果

思路：整数分配问题。我们采用隔板法，隔板法相关例题见这篇博客：https://www.acwing.com/solution/content/241669/。下面开始讲解

利用隔板法推导结果。首先我们考虑当前局面，即只有 i 个苹果的情况下的方案数。于是题目就是 i 个苹果分给 m 个人，允许分到 0 个。于是借鉴上述链接中“少分型”的思路，先借 m 个苹果，那么此时局面中就有 i+m 个苹果，现在就等价于将 i+m 个苹果分给 m 个人，每人至少分得 1 个苹果。（分完以后每个人都还回去就行了），此时的隔板操作就是”标准型”，即 i+m 个苹果产生 i+m-1 个间隔，在其中插 m-1 块板，从而将划分出来的 m 个部分分给 m 个人。此时的划分方案就是 \(C_{i+m-1}^{m-1}\)，那么对于所有的 i，结果就是

\[ \begin{aligned} \sum_{i=1}^n C_{i+m-1}^{m-1} &= C_{m}^{m-1} + C_{m+1}^{m-1} + \cdots + C_{n+m-1}^{m-1} \\ &= C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n} \\ &= (-C_{m}^{0}+C_{m}^{0})+C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n} \\ &= -C_{m}^{0}+(C_{m}^{0}+C_{m}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n}) \\ &= -1+(C_{m+1}^{1} + C_{m+1}^{2} + \cdots + C_{n+m-1}^{n}) \\ &= -1+(C_{m+2}^{2} + \cdots + C_{n+m-1}^{n}) \\ &= -1+C_{n+m}^n \end{aligned} \]

利用乘法逆元计算组合数。结果已经知道了，现在如何计算上述表达式呢？由于 \(n\times m\) 超过了常规递推的组合数计算方法内存空间，因此我们采用乘法逆元的思路计算。值得一提的是，本题在计算某个数关于 1e6+3 的乘法逆元时，不需要判断两者是否互质，因为 1e6+3 是一个质数，并且数据范围中的数均小于 1e6+3，因此两数一定互质，可以直接使用费马小定理计算乘法逆元

时间复杂度：\(O(n\log 1e6)\)

#include <iostream>
using namespace std;
using ll = long long;

const int N = 7e5 + 10;
const int mod = 1e6 + 3;

int fact[N], infact[N];

int qmi(int a, int b, int p) {
    int res = 1 % p;
    while (b) {
        if (b & 1) res = (ll)res * a % p;
        a = (ll)a * a % p;
        b >>= 1;
    }
    return res;
}

void init() {
    fact[0] = 1, infact[0] = 1;
    for (int i = 1; i < N; i++) {
        fact[i] = (ll)fact[i - 1] * i % mod;
        infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
}

int main() {
    init();

    int n, m;
    cin >> n >> m;

    cout << (ll)fact[n + m] * infact[n] % mod * infact[m] % mod - 1;

    return 0;
}

思维题¶

思维题的「例题解析」。

图的遍历

https://www.luogu.com.cn/problem/P3916

题意：给定一个有向图，求解每一个点可以到达的编号最大的点

思路：如果从正向考虑，很显然的一个暴力方法就是对于每一个点都跑一遍 dfs 或者 bfs 获取可达的最大点编号，时间复杂度 \(O(n^2)\)，如果想要在遍历的过程中同时更新其余的点，那只有起点到最大点之间的点可以被更新，可以通过递归时记录路径点进行，时间复杂度几乎不变。我们尝试反向考虑：反向建边。既然正向考虑时需要标记的点为最大点与起点的路径，那不如直接从最大值点开始遍历搜索，在将所有的边全部反向以后，从最大值点开始遍历图，这样就可以在线性时间复杂度内解决问题

时间复杂度：\(O(n+m)\)

bfs 代码

#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
using namespace std;

const int N = 100010;

int n, m;
vector<int> g[N], res(N);

void bfs(int now) {
    queue<int> q;

    res[now] = now;
    q.push(now);

    while (q.size()) {
        int h = q.front();
        q.pop();
        for (auto& ch: g[h]) {
            if (!res[ch]) {
                res[ch] = now;
                q.push(ch);
            }
        }
    }
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        g[b].push_back(a);
    }

    for (int i = n; i >= 1; i--) {
        if (!res[i]) {
            bfs(i);
        }
    }

    for (int i = 1; i <= n; i++) {
        cout << res[i] << ' ';
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

dfs 代码

#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
using namespace std;

const int N = 100010;

int n, m, val;
vector<int> g[N], res(N);

void dfs(int now) {
    res[now] = val;
    for (auto& ch: g[now]) {
        if (!res[ch]) {
            dfs(ch);
        }
    }
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        g[b].push_back(a);
    }

    for (int i = n; i >= 1; i--) {
        if (!res[i]) {
            val = i;
            dfs(i);
        }
    }

    for (int i = 1; i <= n; i++) {
        cout << res[i] << ' ';
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

最长严格递增子序列

https://www.acwing.com/problem/content/5273/

标签：思维、哈希、排序

题意：给定长度为 n 的序列，问将这个序列拼接 n 次后，最长严格递增子序列的长度为多少？

思路：其实最终的思路很简单，将题目转化为在每个序列中选一个数，一共可以选出多少个不同的数。但是在产生这样的想法之前，先讲一下我的思考过程。我将序列脑补出一幅散点折线图，然后将这些点投影到y轴上，最终投影点的个数就是答案的数量，但是投影会有重合，因此答案最多就是 n 个数，最少 1 个数，从而想到就是在 n 个序列中选数，选的数依次增大即可，相应的就是一个求序列不重复数的个数的过程。去重即可。

注意点：由于 C++ 的 STL 的 unique 函数的前提是一个有序的序列，因此在unique之前需要将序列进行排序。

时间复杂度：\(O(n)\)

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int T;
    cin >> T;

    while (T--)
    {
        int n;
        cin >> n;

        vector<int> a;
        for (int i = 0; i < n; i++)
        {
            int x;
            cin >> x;
            a.emplace_back(x);
        }

        sort(a.begin(), a.end());
        a.erase(unique(a.begin(), a.end()), a.end());

        cout << a.size() << endl;
    }

    return 0;
}

三元组

https://www.acwing.com/problem/content/5280/

标签：分讨、组合数学

题意：在一个序列中如何选择一个三元组，使得三个数之积最小，给出情况数

思路：首先很容易得知，这三个数一定是序列排序后的前三个数，那么就是对这三个数可能的情况进行讨论

情况1：前三个数都相等 （2 2 2 2 2 4 5），则就是在所有的 a[0] 中选3个，情况数就是 \(C_{cnt\_a[0]}^{3}\)

情况2：前三个数中有两个数相等，由于数组经过了排序，因此情况2分为两种情况

前两个数相等 （1 1 3 3 3 5），则就是在所有的 a[2] 中选1个，情况数就是 \(C_{cnt\_a[2]}^{1}\)

后两个数相等 （1 2 2 2 4 6），则就是在所有的 a[1] 中选2个，情况数就是 \(C_{cnt\_a[1]}^{2}\)

情况3：前三个数中全都不相等 （1 2 4 4 4 5 7），这就是在所有的 a[2] 中选1个，情况数就是 \(C_{cnt\_a[2]}^{1}\)

可以发现上述情况2的第一种和情况3的答案相等，故分为三种情况即可。

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

// 计算组合数 C_{a}^{b}
ll calc(ll a, ll b) {
    ll fz = 1, fm = 1;
    for (int i = 0, num = a; i < b; i++, num--) {
        fz *= num;
    }
    for (int i = 1; i <= b; i++) {
        fm *= i;
    }
    return fz / fm;
}

int main() {
    int n; cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    sort(a.begin(), a.begin() + n);

    ll res = 0;

    if (a[0] == a[1] && a[1] == a[2]) {
        // 情况1：前三个数都相等（2 2 2 2 2 4 5），则就是在所有的a[0]中选3个
        ll cnt = count(a.begin(), a.begin() + n, a[0]);
        res = calc(cnt, 3);
    } else if (a[0] == a[1] || (a[0] != a[1] && a[1] != a[2])) {
        // 情况2：前两个数相等（1 1 3 3 3 4 5） or 三个数都不相等（1 2 4 4 4 5 7），则就是在所有的a[2]中选2个
        res = count(a.begin(), a.begin() + n, a[2]);
    } else {
        // 情况3：后两个数相等（1 2 2 2 4 6），则就是在所有的a[1]中选2个
        ll cnt = count(a.begin(), a.begin() + n, a[1]);
        res = calc(cnt, 2);
    }

    cout << res << "\n";

    return 0;
}

删除元素

https://www.acwing.com/problem/content/5281/

标签：分讨

题意：给定一个排列为1~n，定义一个数“有价值”为当前数的前面没有数比当前的数大。现在需要删除一个数，使得序列中增加尽可能多的“有价值”的数，如果这个数有多个，则删除最小的那个数

最开始想到的思路：枚举每一个数，如果删除，则序列中会增加多少个“有价值”的数，算法设计如下：

首先判断每一个数是否是有价值的数

创建一个变量来记录当前数的前面序列的最大值

比较判断当前数和前方最大值的关系，如果小于，则无价值，反之有价值

接着枚举每一个数，如果删除该数，则序列会损失多少个有价值的数

首先判断自己是不是有价值的数，如果是，则当前损失值 -1

接着判断删除当前数对后续的影响：我们在枚举后续数的时候，起始的newd（前驱除掉a[i]的最大值）应该就是当前的d，只不过需要使用新变量newd而非d是因为这一步与整体无关，不可以改变整体的d。否则会出现错误，比如对于4 3 5 1 2，如果我们在枚举后续数的时候直接对d进行迭代，那么在第一轮d就会被更新为5，就再也无法更新了

最终根据维护的损失值数组cnt即可求解

时间复杂度 \(O(n^2)\)

优化的思路：

同样是枚举每一个数，如果当前数字是有价值的数，那么cnt[a[i]]就 -1

取决于当前数字前面是否有比它大的数，如果没有，那么就是有价值的

接下来我们不需要遍历j=i+1到j=n-1，而是讨论当前数a[i]不是有价值数时的所有情况。现在我们想要维护cnt数组。不难发现，对于某个位置上的数a[k]，能否成为有价值的数只取决于前排序列是否有比他大的数以及大的数的个数。那么理论上我们在枚举a[i]的时候维护cnt[1~i-1]就可以确保cnt数组的正确性了。

假设a[k]的前排有一个比它大的数d：那么把d去掉之后，a[k]就会从无价值变为有价值

假设a[k]的前排有至少两个比它大的数d1,d2,...dj...：那么不管去掉哪一个 \(d_j\)，我们都没法让a[k]变得有价值

如此一来，cnt数组就可以正确维护了

最终根据维护的损失值数组cnt即可求解

时间复杂度 \(O(n)\)

暴力：

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    // 判断每个数是否是有价值的数
    int d = 0; // 前方序列中的最大值
    vector<bool> is_val(n + 1);
    for (int i = 0; i < n; i++) {
        if (a[i] > d) {
            is_val[a[i]] = true;
            d = a[i];
        }
    }

    // 枚举每一个数，计算删除该数之后会增加的有价值的数的个数 
    d = 0; // 同上
    vector<int> cnt(n + 1); // cnt[x]表示删除数x之后可以增加的有价值的数的个数
    for (int i = 0; i < n; i++) {
        if (is_val[a[i]]) {
            cnt[a[i]]--;
        }

        int newd = d; // 去掉a[i]后的前方序列的最大值 newd
        for (int j = i + 1; j < n; j++) {
            if (is_val[a[j]]) {
                if (a[j] < newd) {
                    cnt[a[i]]--;
                }
            } else {
                if (a[j] > newd) {
                    cnt[a[i]]++;
                }
            }
            if (a[j] > newd) {
                newd = a[j];
            }
        }

        // 更新前方序列的最大值 d
        if (a[i] > d) {
            d = a[i];
        }
    }

    // 找出可以增加的有价值的数的最大个数 ma
    int ma = -n - 1;
    for (int i = 0; i < n; i++) {
        if (cnt[a[i]] > ma) {
            ma = max(ma, cnt[a[i]]);
        }
    }

    // 答案是满足个数的最小的数字
    int res = 0;
    for (int i = 1; i <= n; i++) {
        if (cnt[i] == ma) {
            res = i;
            break;
        }
    }

    cout << res << "\n";

    return 0;
}

优化：

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n; 
    cin >> n;

    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<int> cnt(n + 1);     // cnt[x]表示删除数x之后可以增加的有价值的数的个数
    int d1 = 0, d2 = 0;         // d1: 最大值, d2: 次大值
    for (int i = 0; i < n; i++) {
        if (a[i] > d1) {
            // 前方序列 没有数比当前的数大
            cnt[a[i]]--;
        } else if (a[i] > d2) {
            // 前方序列 只有一个数比当前大
            cnt[d1]++;
        }

        // 更新最大值d1和次大值d2
        if (a[i] > d1) d2 = d1, d1 = a[i];
        else if (a[i] > d2) d2 = a[i];
    }

    // 找到可以增加的最大值
    int ma = -1;
    for (int i = 1; i <= n; i++) {
        if (cnt[i] > ma) {
            ma = cnt[i];
        }
    }

    // 取元素的最小值
    int res = n + 1;
    for (int i = 1; i <= n; i++) {
        if (cnt[i] == ma) {
            res = i;
            break;
        }
    }

    cout << res << "\n";

    return 0;
}

Sorting with Twos

https://codeforces.com/contest/1891/problem/A

标签：构造

题意：给定一个序列，现在需要通过以下方法对序列进行升序排序

可以选择前 \(2^m\) 个数执行 \(-1\) 的操作（保证不会越界的情况下）

现在需要确定给定的序列经过k次上述后能否变为升序序列

思路：我们可以将每 \(2^k\) 个数看成一个数，可以不断的-1。那么可以发现执行一定的次数后，一定可以实现升序序列。但是现在是 \(2^k\) 个数，那么只需要这相邻区段的数是升序即可，即 \(2^{k-1} \to 2^k\) 之间的数是升序即可。按区间进行判断即可

时间复杂度：\(O(n)\)

void judge(vector<int>& a, int l, int r, bool& ok, int n) {
    for (int i = l + 1; i <= r && i <= n; i++) {
        if (a[i] < a[i - 1]) {
            ok = false;
            return;
        }
    }
}

void solve() {
    int n;
    cin >> n;

    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    bool ok = true;
    judge(a, 3, 4, ok, n);
    judge(a, 5, 8, ok, n);
    judge(a, 9, 16, ok, n);
    judge(a, 17, 20, ok, n);

    if (ok) {
        cout << "YES\n";
    } else {
        cout << "NO\n";
    }
}

指针运动

https://www.acwing.com/problem/content/description/5468

标签：模拟

题意：给定一个序列，和一个从第一个数开始的指针，若当前指的数为 0 则输出当前数的下标结束程序，若不为 0 则全体正数减一并将指针后移，若指针越界则重新指向第一个数。问最终指向第几个数

思路： - 第一层思路：纯暴力。即按照题意进行模拟，时间复杂度 \(O(n \times \max (a_i))\) - 第二层思路：枚举优化。假设当前枚举到了第 k 次，若第一次遇到当前的数小于 k，则该数就是终止指向的数，时间复杂度 \(O(n \times \max(a_i))\) - 第三层思路：数列优化。

套餐设计

https://www.acwing.com/problem/content/5480/

标签：哈希

题意：给定 n 个食物，其中可能有相同种类的，现在需要设计一个食物套餐包含 k 个食物，问如何设计套餐可以使得产生的套餐数最多，给出最多数量的套餐数

思路：如果不限定套餐中食物的种类数，那么我们可以从最多可生产的套餐数 \(\left \lfloor \frac{n}{k} \right \rfloor\) 开始降序检查，直到一套都无法生产为止（即一套需要的食物数超过了总的食物数）。检查的逻辑很简单，我们知道对于当前的套餐数 \(i\)，每一种食物的数量如果超过了 \(i\)，就至少可以对套餐贡献 \(1\) 个食物的数量。我们统计当前需要套餐数的局面下，所有食物可以贡献的食物数量 \(cnt\)，如果超过了需要的套餐数 \(i\)，显然是可以满足需求的套餐数的。为了求得最大的套餐数，从降序开始检查直到可以满足即可。

时间复杂度：\(O(n^2)\)

#include <iostream>
#include <unordered_map>
using namespace std;
typedef long long ll;

const int N = 110;

int n, k, a[N];
unordered_map<int, int> v;

void solve() {
    cin >> k >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        v[a[i]]++;
    }

    int res = 0;

    int i; // 当前需要生产的套餐数
    for (i = n / k; i >= 1; i--) {
        // 所有食物对于当前套餐需要的食物数量可以贡献的最大食物数量
        int cnt = 0; 
        for (auto& x: v) {
            // 每种食物对于当前套餐需要的食物数量可以贡献的最大食物数量
            cnt += x.second / i;
        }
        if (cnt >= k) {
            res = i;
            break;
        }
    }

    cout << res << "\n";
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int T = 1;
//    cin >> T;
    while(T--) solve();
    return 0;
}

分班

https://www.acwing.com/problem/content/5481/

标签：贪心、分讨

题意：给定 \(n \times k\) 个学生，需要将这些学生分成 \(n\) 组，每组 \(k\) 个人，第 \(i\) 个学生有一个属性值 \(a_i\) 。问如何分组可以使得在满足任意两组学生中最小值相差不超过 \(lim\) 的情况下，所有组最小值之和最大，给出这个最大值

思路：一开始觉得是二分答案，但是不知道在已知答案的情况下如何检查，因为我不知道应该如何分组最优，未遂。重读题目发现题中的 lim 约束不是相邻两组，而是任意两组，思路打开，那我直接根据这个条件将满足约束的所有学生枚举出来（很显然是相对于数值最小的学生而言），然后设计如何将这些学生安排到 n 组且保证他们是组里最小的即可。先看下面的学生编号 - 学生属性示意图：

很显然我们需要将这 \(n \times k\) 个学生按数值升序排序，为了满足任意两组的最小值不超过 \(lim\)，我们找到前 \(r\) 个学生满足比最小的学生超过的数不超过 \(lim\) 即可。接下来就是从这 \(r\) 个学生中选择出 \(n\) 个安排到 \(n\) 个组中，即可满足题中 \(lim\) 的限制，现在就是考虑如何分组可以使得答案最大了。不难发现一共有三种情况

\(r<n\) ：即可选择人数都没有组数多。那么分完组以后肯定无法满足任意两组的最小值不超过 \(lim\)，直接输出 \(0\) 即可

\(r=n\) ：即可选择人数和组数相等。这种情况最好理解，就是将这 \(r(n)\) 个人安排到 \(n\) 组，答案就是这 \(r(n)\) 个人数值之和

\(r>n\) ：即可选择人数多于组数。如果纯粹的贪心，将第一个人放在第一组，然后从第 \(r\) 个人开始将 \(n-1\) 个人安排在剩余的 \(n-1\) 组。这样的确可以满足答案最大，但是忽略了一个点就是从第 \(2\) 个人开始的 \(r-n\) 个人何去何从？如果全部安排到了第一组那万事大吉，如果第一组塞不进去就不得不安排到别的组，这样答案就不是上面计算的结果了，应该更小才对！那么应该如何解决这个问题呢？我们可以从往第一组塞剩余的人得到启发：如果第一组可以容纳剩余的人活着还有空位就已经满足了第二种情况，就可以直接计算结果，如果第一组无法容纳从第 \(2\) 个人开始的 \(r-n\) 个人，就将第 \(1+k\) 个人作为一组的最小值，继续贪心的容纳紧跟着的人，从而确保剩下的人数值尽可能的大。如此循环知道出现 剩余的人的数量=还未安排最小值的组的数量 为止，计算答案总和即可！

时间复杂度：\(O(n \log n)\)

#include <iostream>
using namespace std;
typedef long long ll;

const int N = 1e5 + 10;

ll n, k, lim, a[N];

void solve() {
    cin >> n >> k >> lim;

    int num = n * k;

    for (int i = 1; i <= num; i++) cin >> a[i];

    sort(a + 1, a + num + 1);

    // 找到最大的满足 lim 限制的人的下标 r - 线性或二分均可
    int l = 1, r = num;
    while (l < r) {
        int mid = (l + r + 1) >> 1;
          if (a[mid] <= a[1] + lim) l = mid;
          else r = mid - 1;
    }

    ll res = 0;

    if (r < n) res = 0;
    else {
        res += a[1];
        int idx = 2;   // 指针
        int in = 1;    // 已安排作为组内最小值的人员数
        int team = 1;  // 当前组内的人员数
        while (r - idx + 1 > n - in) { // 当可选择人数多于组数时
            if (team < k) team++, idx++; // 塞得下就继续塞
            else team = 1, res += a[idx], idx++, in++; // 塞不下就重开一组
        }
        for (int i = idx; i <= r; i++) {
            res += a[i];
        }
    }

    cout << res << "\n";
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int T = 1;
//    cin >> T;
    while(T--) solve();
    return 0;
}

双端队列

https://www.acwing.com/problem/content/5484/

标签：贪心、分讨

题意：给定一个序列，每次可以从序列头或尾取出一个数，在满足：按取出数的顺序是升序序列的条件下，给定的序列最多可以取出多少数？

思路：首先很容易想到的就是哪头小取哪头，因为取了较小者后较大者可以后续继续被选择，反之则不能。当然，还需要考虑的一个点就是如果较小者不符合题意，即较小者比上一次选出来的数更小从而无法组成严格升序序列时，还是得考虑较大值的那一头数。接下来考虑相等的情况，若两头数值相等，那一定只能选择一端且后续都只能从那端继续选择，我们直接两种方法都计算统计一遍可选择的数的数量，取较大者即可

时间复杂度：\(O(n)\)

#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <stack>
using namespace std;

const int N = 200010;

int n, a[N];

void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    int res = 0, top = -1, l = 1, r = n;
    while (l <= r) {
        // 左端是较小值
        if (a[l] < a[r]) {
            if (a[l] > top) {
                res++;
                top = a[l++];
            } else if (a[r] > top) {
                res++;
                top = a[r--];
            } else {
                break;
            }
        // 右端是较小值
        } else if (a[l] > a[r]) {
            if (a[r] > top) {
                res++;
                top = a[r--];
            } else if (a[l] > top) {
                res++;
                top = a[l++];
            } else {
                break;
            }
        // 两端数值相等
        } else { // a[l] == a[r]
            if (a[l] > top) {
                int lcnt = 1, rcnt = 1;
                for (int i = l + 1; i <= r; i++) {
                    if (a[i] > a[i - 1]) lcnt++;
                    else break;
                }
                for (int i = r - 1; i >= l; i--) {
                    if (a[i] > a[i + 1]) rcnt++;
                    else break;
                }
                res += max(lcnt, rcnt);
                break;
            } else {
                break;
            }
        }
    }

    cout << res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

你说的对，但是这是签到 I

https://hydro.ac/d/nnu_contest/p/P1201

题意：给定两个单调不减且只含有小写字母的字符串，求解其中最长公共子串长度

思路：

一眼 dp？错误的，那时间复杂度就是 \(O(n^2)\)，显然不可能。可以发现与常规的最长公共子串的题目不同，本题中两个字符串是单调的，这个性质一定很有用。事实的确如此。

对于单调的两个字符串而言，如果连续的字符数量之和相等，即对于 \(c_i,c_j\) 之间的所有的字符对应的数量都相等 \(a[c_k]=b[c_k],(k=i+1,i+1, \cdots,j-1)\)，则该段字符串就一定是公共子串。答案就是 \(\displaystyle \sum_{k=i+1}^{j-1}a[c_k]\) 或 \(\displaystyle \sum_{k=i+1}^{j-1}b[c_k]\)。在枚举字符时，需要特判一下只有一种字符的情况。

时间复杂度：\(\Theta(n + 26^3)\)

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#include <set>
using namespace std;

const int N = 26;

string s, t;
int a[N], b[N];

void solve() {
    cin >> s >> t;

    for (auto c: s) a[c - 'a']++;
    for (auto c: t) b[c - 'a']++;

    int res = -1;

    for (int i = 0; i < N; i++) {
        for (int j = i; j < N; j++) {
            if (j == i) res = max(res, min(a[i], b[j]));
            else {
                bool ok = true;
                int mid = 0;
                for (int k = i + 1; k <= j - 1; k++) {
                    if (a[k] != b[k]) ok = false;
                    mid += a[k];
                }

                if (ok) {
                    res = max(res, min(a[i], b[i]) + mid + min(a[j], b[j]));
                }
            }
        }
    }

    cout << res << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

从双倍数组中还原原数组

https://leetcode.cn/problems/find-original-array-from-doubled-array/description/

标签：贪心

题意：给定一个改变后数组，问其原始数组是什么？我们定义改变后数组为原始数组每一个元素乘以2以后加入原始数组，并随机打乱得到的数组

思路：答案与下标无关，我们考虑对原始数组升序排序。在哈希统计每一个元素出现的频率后，可以枚举每一个元素，如果当前元素与当前元素的二倍都存在，则说明当前元素一定存在于原始数组中，我们将其加入答案并对两个数的频率统计减一。

时间复杂度：\(O(n\log n)\)

class Solution {
public:
    vector<int> findOriginalArray(vector<int>& changed) {
        vector<int> res;

        // 剪枝：合法原始数组一定是偶数个
        int n = changed.size();
        if (n & 1) return {};

        sort(changed.begin(), changed.end());
        unordered_map<int, int> cnt;
        for (int x: changed) cnt[x]++;

        for (int x: changed) {
            if (cnt[x] == 0) continue;

            cnt[x]--;
            if (cnt[x * 2]) {
                cnt[x * 2]--;
                res.push_back(x);
            }
            else {
                return {};
            }
        }

        return res;
    }
};

可获得的最大点数

https://leetcode.cn/problems/maximum-points-you-can-obtain-from-cards/description/

题意：给定一个序列，每次可以从头或尾取一个元素并弹出该元素，问如何取数可以使得取到的数总和最大

思路：前缀和、双指针。很显然，我们选到的数的组成一定是原数组的头部一部分和尾部一部分，从反面思考，其实就是让中间一部分的数值总和最小！因此我们用前缀和记录一下然后双指针枚举序列即可。之所以记录本地是因为双指针好久没写了，调了好久 : (

时间复杂度：\(O(n)\)

class Solution {
public:
    int maxScore(vector<int>& cardPoints, int k) {
        int n = cardPoints.size();
        vector<int> s(n + 1, 0);
        for (int i = 1; i <= n; i++) {
            s[i] = s[i - 1] + cardPoints[i - 1];
        }

        int res = -1;
        int l = 1, r = l + n - k - 1;
        while (r <= n) {
            res = max(res, s[n] - (s[r] - s[l - 1]));
            l++, r++;
        }

        return res;
    }
};

确定两个字符串是否接近

https://leetcode.cn/problems/determine-if-two-strings-are-close/description/

题意：给定两个字符串，可以对两个字符串进行任意次下面的操作：问在操作后使得两个字符串完全相等

交换一个字符串中的任意两个字符

交换一个字符串中的任意两个相同字符的集合。比如 \(\underline {aa} c \underline{abb} \to \underline{bb}c\underline{baa}\)

思路：一道纯纯思维题。首先对于第一个操作，我们可以直接对两个字符串排序即可，至于第二个操作，我们需要确保两个字符串哈希值中，所有的键全部相等，即两个字符串排序去重后应该完全相等，同时还需要确保两个字符串哈希的结果中值排序的结果完全相等，这样就可以通过操作二使得两个字符串完全相等

时间复杂度：\(O(n \log n)\)

class Solution {
public:
    bool closeStrings(string word1, string word2) {
        // 剪枝：两个字符串长度不相等，则操作后一定不可能相等
        if (word1.size() != word2.size()) return false;

        // 执行操作1
        sort(word1.begin(), word1.end());
        sort(word2.begin(), word2.end());

        // 剪枝：若两个字符串排序后相等就不需要执行操作2了，已经相等了
        if (word1 == word2) return true;

        // 哈希两个字符串的字符与对应字符数量
        unordered_map<char, int> a, b;
        for (auto& c: word1) a[c]++;
        for (auto& c: word2) b[c]++;

        // 剪枝：字符种类数不一样，则操作2后一定不可能相等
        if (a.size() != b.size()) return false;

        // 剪枝：字符种类数一样但是种类不一样，则操作2后一定不可能相等
        for (auto it: a) {
            if (b[it.first] == 0) {
                return false;
            }
        }

        // 执行操作2：比较所有种类字符的数量
        vector<int> va, vb;
        for (auto& it: a) va.push_back(it.second);
        for (auto& it: b) vb.push_back(it.second);
        sort(va.begin(), va.end());
        sort(vb.begin(), vb.end());
        return va == vb;
    }
};

同位字符串连接的最小长度

https://leetcode.cn/problems/minimum-length-of-anagram-concatenation/

题意：给定一个由若干个同位字符串 t 组成的字符串 s，问这个同位字符串最短是什么？定义同位字符串为字符数量相等且每种字符的数量相等的字符串

错误思路：很显然的一个分配问题。我们预统计每一种字符的数量，假设答案同位字符串长度为 len，则显然就需要将所有的字符等分为 s.size() / len 份，每一份的每一种字符数量均相等。也就是每一种字符都需要分为 s.size() / len 份。为了最小化 len，就需要分出尽可能多的同位字符串。每一种字符可以分出的份数是其因数，取所有字符可分出份数的最大值就是求解每一种字符数量的最大公因数！于是问题就转化为了求解每一种字符数量的最大公因数

时间复杂度：\(O(n)\)

正确思路：上述思路忽略了同位字符串必须存在于原始字符串中这个约束。正确做法就更加无脑了，直接枚举字符串 s 的每一个因数，然后检查所有长度的子串是否可以作为同位字符串即可

时间复杂度：\(O(128 \times n)\)

WA code

class Solution {
public:
    int minAnagramLength(string s) {
        unordered_map<char, int> a;
        for (auto c: s) a[c]++;

        vector<int> v;
        for (auto& it: a) v.push_back(it.second);

        int gcd;
        if (v.size() == 1) gcd = v[0];
        else {
            gcd = __gcd(v[0], v[1]);
            for (int i = 2; i < v.size(); i++) {
                gcd = __gcd(gcd, v[i]);
            }
        }

        return s.size() / gcd;
    }
};

AC code

class Solution {
public:
    int minAnagramLength(string s) {
        int n = s.size();

        vector<int> v;
        for (int i = 1; i <= n / i; i++) {
            if (n % i == 0) {
                v.push_back(i);
                v.push_back(n / i);
            }
        }

        int res = n + 1;

        for (int len: v) {
            bool ok = true;

            string pre = s.substr(0, len);
            sort(pre.begin(), pre.end());
            for (int i = len; i <= n - len; i += len) {
                string now = s.substr(i, len);
                sort(now.begin(), now.end());
                if (now != pre) {
                    ok = false;
                    break;
                }
            }

            if (ok) {
                res = min(res, len);
            }
        }

        return res;
    }
};

进阶算法

前言¶

动态规划¶

递推¶

线性 dp¶

网格图dp¶

树形dp¶

高维dp¶

区间dp¶

状压dp¶

图论¶

拓扑¶

二分图¶

最小生成树¶

最短路¶

最近公共祖先¶

博弈论¶

计算几何¶

数论¶

质数¶

整除¶

组合数学¶

思维题¶