graphs

本文最后更新于 2024年7月25日 中午

图论

【拓扑】有向图的拓扑序列

https://www.acwing.com/problem/content/850/

题意：输出一个图的拓扑序，不存在则输出-1

思路：

  • 首先我们要知道拓扑图的概念，感官上就是一张图可以从一个方向拓展到全图，用数学语言就是：若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列
  • 接着我们就想要寻找这样的序列 A 了，可以发现对于每一个可扩展的点，入度一定为0，那么我们就从这些点开始宽搜，将搜到的点的入度-1，即删除这条边，直到最后。如果全图的点的入度都变为了0，则此图可拓扑

时间复杂度：O(n+m)O(n+m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int n, m;
vector<int> G[N];

void solve() {
    // 建图 
    cin >> n >> m;
    vector<int> d(n + 1, 0);
    for (int i = 1; i <= m; i++) {
        int a, b;
        cin >> a >> b;
        d[b]++;
        G[a].push_back(b);
    }
    
    // 预处理宽搜起始点集
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (!d[i])
            q.push(i);
    
    // 宽搜处理
    vector<int> res;
    while (q.size()) {
        auto h = q.front();
        q.pop();
        res.push_back(h);
        
        for (auto& ch: G[h]) {
            d[ch]--;
            if (!d[ch]) q.push(ch);
        }
    }
    
    // 输出合法拓扑序
    if (res.size() == n) {
        for (auto& x: res) {
            cout << x << " ";
        }
    } else {
        cout << -1 << "\n";
    }
}

int main() {
    solve();
    return 0;
}

【基环树/拓扑】Mad City🔥

https://codeforces.com/contest/1873/problem/H

tag：基环树、拓扑排序

题意：给定一个基环树，现在图上有两个点，分别叫做A，B。现在B想要逃脱A的抓捕，问对于给定的局面，B能否永远逃离A的抓捕

思路：思路很简单，我们只需要分B所在位置的两种情况讨论即可

  1. B不在环上：此时我们记距离B最近的环上的那个点叫 tagtag，我们需要比较的是A到tag点的距离 dAd_A 和B到tag的距离 dBd_B，如果 dB<dAd_B < d_A，则一定可以逃脱，否则一定不可以逃脱
  2. B在环上：此时我们只需要判断当前的A点是否与B的位置重合即可，如果重合那就无法逃脱，反之B一定可以逃脱。

代码实现：

  1. 对于第一种情况，我们需要找到tag点以及计算A和B到tag点的距离，

时间复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
using namespace std;

const int N = 200010;

int n, a, b;
vector<int> G[N];
int rd[N], tag, d[N];
bool del[N], vis[N];

void init() {
    for (int i = 1; i <= n; i++) {
        G[i].clear();        // 存无向图 
        rd[i] = 0;            // 统计每一个结点的入度 
        del[i] = false;        // 拓扑删点删边时使用 
        d[i] = 0;            // 图上所有点到 tag 点的距离 
        vis[i] = false;        // bfs计算距离时使用 
    }
}

void topu(int now) {
    if (rd[now] == 1) {
        rd[now]--;
        del[now] = true;
        for (auto& ch: G[now]) {
            if (del[ch]) continue;
            rd[ch]--;
            if (now == tag) {
                tag = ch;
            }
            topu(ch);
        }
    }
}

void bfs() {
    queue<int> q;
    q.push(tag);
    d[tag] = 0;
    
    while (q.size()) {
        auto now = q.front();
        vis[now] = true;
        q.pop();
        
        for (auto& ch: G[now]) {
            if (!vis[ch]) {
                d[ch] = d[now] + 1;
                q.push(ch);
                vis[ch] = true;
            }
        }
    }
}

void solve() {
    // 初始化
    cin >> n >> a >> b; 
    init();
    
    // 建图 
    for (int i = 1; i <= n; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v), rd[v]++;
        G[v].push_back(u), rd[u]++;
    }
    
    // 拓扑删边 & 缩b点
    tag = b;
    for (int i = 1; i <= n; i++) {
        topu(i);
    }

    // 判断结果 & 计算距离 
    if (rd[b] == 2 && a != b) {
        // b点在环上
        cout << "Yes\n";
    } else {
        // b不在环上
        bfs();
        cout << (d[a] > d[b] ? "Yes\n" : "No\n");
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T = 1;
    cin >> T;
    while (T--) solve();
    return 0;
}

【二分图】染色法判定二分图

https://www.acwing.com/problem/content/862/

题意：给定一个无向图，可能有重边和自环。问是否可以构成二分图。

二分图的定义：一个图可以被分成两个点集，每个点集内部没有边相连（可以不是连通图）

思路：利用染色法，遍历每一个连通分量，选择连通分量中的任意一点进行染色扩展

  • 如果扩展到的点没有染过色，则染成与当前点相对的颜色
  • 如果扩展到的点已经被染过色了且染的颜色和当前点的颜色相同，则无法构成二分图（奇数环）

时间复杂度：O(n+e)O(n+e)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
const int N = 100010;

int n, m;
vector<int> G[N], col(N);

bool bfs(int u) {
    queue<int> q;
    q.push(u);
    col[u] = 1;

    while (q.size()) {
        int now = q.front();
        q.pop();
        for (auto& ch: G[now]) {
            if (!col[ch]) {
                col[ch] = -col[now];
                q.push(ch);
            }
            else if (col[ch] == col[now]) {
                return false;
            }
        }
    }

    return true;
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }

    // 遍历每一个连通分量
    for (int i = 1; i <= n; i++) {
        if (!col[i]) {
            bool ok = bfs(i);
            if (!ok) {
                cout << "No\n";
                return;
            }
        }
    }

    cout << "Yes\n";
}

【最小生成树】Kruskal算法求最小生成树

https://www.acwing.com/problem/content/861/

题意：给定一个无向图，可能含有重边和自环。试判断能否求解其中的最小生成树，如果可以给出最小生成树的权值

思路：根据数据量，可以发现顶点数很大，不适用 PrimPrim 算法，只能用 KruskalKruskal 算法，下面简单介绍一下该算法的流程

  • 自环首先排除 - 显然这条边连接的“两个”顶点是不可能选进 MSTMST 的
  • 首先将每一个结点看成一个连通分量
  • 接着按照权值将所有的边升序排序后，依次选择
    • 如果选出的这条边的两个顶点不在一个连通分量中，则选择这条边并将两个顶点所在的连通分量合并
    • 如果选出的这条边的两个顶点在同一个连通分量中，则不能选择这条边（否则会使得构造的树形成环）
  • 最后统计选择的边的数量 numnum 进行判断即可
    • num=n−1num=n-1，则可以生成最小生成树
    • num<n−1num<n-1，则无法生成最小生成树
  • 时间复杂度：O(elog⁡e)O(e\log e)​ - 因为最大的时间开销在对所有的边的权值进行排序上

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 100010;

struct edge {
    int a, b;
    int w;
};

int n, m;
vector<edge> edges;
vector<int> p(N);

int Find(int now) {
    if (p[now] != now) {
        p[now] = Find(p[now]);
    }
    return p[now];
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        if (a == b) {
            continue;
        }
        edges.push_back({a, b, w});
    }

    // 按照边权升序排序
    sort(edges.begin(), edges.end(), [&](edge& x, edge& y) {
        return x.w < y.w;
    });

    // 选边
    for (int i = 1; i <= n; i++) {
        p[i] = i;
    }

    int res = 0, num = 0;

    for (auto& e: edges) {
        int pa = Find(e.a), pb = Find(e.b);
        if (pa != pb) {
            num++;
            p[pa] = pb;
            res += e.w;
        }

        if (num == n - 1) {
            break;
        }
    }

    // 特判：选出来的边数无法构成一棵树
    if (num < n - 1) {
        cout << "impossible\n";
        return;
    }

    cout << res << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def Find(x: int, p: list) -> int:
    if p[x] != x: p[x] = Find(p[x], p)
    return p[x]

def kruskal(n: int, m: int, edges: list) -> int:
    # 按边权对边进行降序排序
    edges.sort(key=lambda edge: edge[-1])

    # dsu 初始化
    p = [None] + [i for i in range(1, n + 1)]

    # 选边
    cnt = sum = 0
    for edge in edges:
        if cnt == n - 1: break

        pa, pb = Find(edge[0], p), Find(edge[1], p)
        if pa != pb:
            p[pa] = pb
            cnt += 1
            sum += edge[2]

    return sum if cnt == n - 1 else 0


if __name__ == "__main__":
    n, m = map(int, input().split())

    edges = []
    for i in range(m):
        edge = tuple(map(int, input().split()))
        edges.append(edge)

    res = kruskal(n, m, edges)

    if res: print(res)
    else: print("impossible")

JavaScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
const readline = require('readline');
const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout,
});

let n = null;
let m = null;
const edges = [];

rl.on('line', line => {
    const [a, b, c] = line.split(' ').map(i => Number(i));
    if (n === null) {
        n = a;
        m = b;
    } else {
        edges.push([a, b, c]);
    }
});

rl.on('close', () => {
    const res = kurskal(n, m, edges);
    console.log(res === Infinity ? 'impossible' : res);
});

function Find(x, p) {
    if (p[x] != x) p[x] = Find(p[x], p);
    return p[x];
}

function kurskal(n, m, edges) {
    // 对边进行升序排序
    edges.sort((a, b) => a[2] - b[2]);
    
    // 初始化 dsu
    p = [];
    for (let i = 1; i <= n; i++) p[i] = i;
    
    // 选边
    let cnt = 0, sum = 0;
    for (let [a, b, w] of edges) {
        if (cnt == n - 1) {
            break;
        }
        
        let pa = Find(a, p), pb = Find(b, p);
        if (pa !== pb) {
            cnt++;
            p[pa] = pb;
            sum += w;
        }
    }
    
    if (cnt === n - 1) return sum;
    else return Infinity;
}

【最小生成树】Prim算法求最小生成树

https://www.acwing.com/problem/content/860/

题意：给定一个稠密无向图，有重边和自环。求出最小生成树

思路：根据题目的数据量，可以使用邻接矩阵存储的方法配合 PrimPrim 算法求解最小生成树，下面给出该算法的流程

  • 首先明确一下变量的定义：
    • g[i][j] 为无向图的邻接矩阵存储结构
    • MST[i] 表示 ii 号点是否加入了 MSTMST 集合
    • d[i] 表示 i 号点到 MSTMST 集合的最短边长度
  • 自环不存储，重边只保留最短的一条
  • 任选一个点到集合 MSTMST 中，并且更新 dd 数组
  • 选择剩余的 n−1n-1 个点，每次选择有以下流程
    • 找到最短边，记录最短边长度 ee 和相应的在 U−MSTU-MST 集合中对应的顶点序号 vv
    • 将 vv 号点加入 MSTMST 集合，同时根据此时选出的最短边的长度来判断是否存在最小生成树
    • 根据 vv 号点，更新 dd 数组，即更新在集合 U−MSTU-MST 中的点到 MSTMST 集合中的点的交叉边的最短长度
  • 时间复杂度：O(n2)O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 510;

int n, m;
vector<vector<int>> g(N, vector<int>(N, INT_MAX));
vector<int> d(N, INT_MAX); // d[i]表示i号点到MST集合中的最短边长度
bool MST[N];
int res;

void prim() {
    // 选任意一个点到MST中并更新d数组
    MST[1] = true;
    for (int i = 1; i <= n; i++)
        if (!MST[i])
            d[i] = min(d[i], g[i][1]);

    // 选剩下的n-1个点到MST中
    for (int i = 2; i <= n; i++) {
        // 1. 找到最短边
        int e = INT_MAX, v = -1; // e: 最短边长度，v: 最短边不在MST集合中的顶点
        for (int j = 1; j <= n; j++)
            if (!MST[j] && d[j] < e)
                e = d[j], v = j;

        // 2. 加入MST集合
        MST[v] = true;
        if (e == INT_MAX) {
            // 特判无法构造MST的情况
            cout << "impossible\n";
            return;
        } else {
            res += e;
        }

        // 3. 更新交叉边 - 迭代（覆盖更新）
        for (int j = 1; j <= n; j++)
            if (!MST[j])
                d[j] = min(d[j], g[j][v]);
    }

    cout << res << "\n";
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;

        if (a == b) {
            continue;
        }

        if (g[a][b] == INT_MAX) {
            g[a][b] = w;
            g[b][a] = w;
        } else {
            g[a][b] = min(g[a][b], w);
            g[b][a] = min(g[b][a], w);
        }
    }

    prim();
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

【最短路】Dijkstra求最短路 🔥

朴素版 - https://www.acwing.com/problem/content/851/

堆优化 - https://www.acwing.com/problem/content/852/

题意：给定一个正边权的有向图，可能存在重边与自环，问 11 号点到 nn 号点的最短路径长度是多少，如果不可达就输出 −1-1。

思路一：朴素版。点数 1≤n≤5001\le n \le 500，边数 1≤m≤1051 \le m\le 10^5

  • 思路：根据数据量，我们采用邻接矩阵的方式存储「点少边多」的稠密图。我们定义 d[i] 数组表示起点到 i 号点的最短距离。先将起点放入 SPT (Shortest Path Tree) 集合，然后更新所有 V-SPT 中的点到 SPT 集合的最短路径长度。接着循环 n-1 次迭代更新剩余的 n-1 个点，每次迭代的过程中，首先选择距离起点最近的点 vex，然后将该点加入 SPT 集合，最后利用该点更新 V-SPT 集合中和该点有连边的点到起点的最短距离。最终的 d[end] 就是起点 start 到终点 end 的最短距离。

  • 总结：算法整体采用贪心与动态规划的思路。与 Prim\text{Prim} 算法仔细比对可知，其中的贪心过程几乎一致，即每次选择加入 SPT 集合的点均为当前局面 V-SPT 集合中距离起点最近的点。而动态规划的过程体现在，在求解出集合 V-SPT 中到集合 STP 最短距离的点 vex 之后，利用该点对「在 V-SPT 集合且和 vex 点有连边的点 i」更新 d[i] 的过程。更新前的状态都是在之前的子结构下的最优解。

  • 时间复杂度：O(n2)O(n^2)

思路二：堆优化。点数 1≤n≤1.5×1051\le n \le 1.5 \times 10^5，边数 1≤m≤1.5×1051 \le m \le 1.5 \times 10^5

  • 思路：根据数据量，我们采用邻接表的方式存储「点多边少」的稀疏图。如果采用上述朴素 Dijkstra 算法进行求解必然会因为点数过多而超时，因此我们利用数据结构「堆」进行时间开销上的优化。不难发现朴素 Dijkstra 算法在迭代过程中主要有三部分：

    1. 选择距离起点最近的点 vex。因为需要枚举所有的顶点，因此总的时间复杂度为 O(n2)O(n^2)
    2. 将该点加入 SPT 集合。因为只是简单的打个标记，因此总的时间复杂度为 O(n)O(n)
    3. 利用该点更新 V-SPT 集合中和该点相连的点到起点的最短距离。因为此时枚举的是该点所有的连边，而邻接表的图存储方式无法进行重边的删除，因此最坏情况下会枚举所有的边，时间复杂度为 O(m)O(m)

  • 时间复杂度：

朴素版C++：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>

using ll = long long;
using namespace std;

int dijkstra_ori(std::vector<std::vector<int>>& g, int start, int end) {
    int n = g.size() - 1;
    std::vector<int> d(n + 1, INT_MAX >> 1);
    std::vector<bool> SPT(n + 1, false);
    
    // update start vex
    d[start] = 0;
    SPT[start] = true;
    for (int i = 1; i <= n; i++) {
        if (!SPT[i] && g[start][i] != INT_MAX >> 1) {
            d[i] = std::min(d[i], d[start] + g[start][i]);
        }
    }
    
    // update remain n-1 vex
    for (int k = 0; k < n - 1; k++) {
        int vex = -1;
        for (int i = 1; i <= n; i++) {
            if (!SPT[i] && (vex == -1 || d[i] < d[vex])) {
                vex = i;
            }
        }
        SPT[vex] = true;
        for (int i = 1; i <= n; i++) {
            if (!SPT[i] && g[vex][i] != INT_MAX >> 1) {
                d[i] = std::min(d[i], d[vex] + g[vex][i]);
            }
        }
    }
    
    return d[end] == INT_MAX >> 1 ? -1 : d[end];
}

void solve() {
    int n, m;
    cin >> n >> m;
    
    vector<vector<int>> g(n + 1, vector<int>(n + 1, INT_MAX >> 1));
    
    while (m--) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u][v] = min(g[u][v], w);
    }
    
    cout << dijkstra_ori(g, 1, n) << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T = 1;
//    std::cin >> T;
    while (T--) solve();
    return 0;
}

朴素版Python：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import heapq
from collections import defaultdict
from typing import List, Tuple
import math
from itertools import combinations

II = lambda: int(input())
FI = lambda: float(input())
MII = lambda: tuple(map(int, input().split()))
LII = lambda: list(map(int, input().split()))


def dijkstra_ori(g: List[List[int]], start: int, end: int) -> int:
    n = len(g) - 1
    d = [10 ** 5] * (n + 1)
    SPT = [False] * (n + 1)
    
    d[start] = 0
    SPT[start] = True
    for i in range(1, n + 1):
        if not SPT[i] and g[start][i] != 10 ** 5:
            d[i] = min(d[i], d[start] + g[start][i])
    
    for _ in range(n - 1):
        vex = -1
        for i in range(1, n + 1):
            if not SPT[i] and (vex == -1 or d[i] < d[vex]):
                vex = i
        SPT[vex] = True
        for i in range(1, n + 1):
            if not SPT[i] and g[vex][i] != 10 ** 5:
                d[i] = min(d[i], d[vex] + g[vex][i])
    
    return -1 if d[end] == 10 ** 5 else d[end]


def solve() -> None:
    n, m = MII()
    g = [[10 ** 5] * (n + 1) for _ in range(n + 1)]
    for _ in range(m):
        u, v, w = MII()
        g[u][v] = min(g[u][v], w)
    print(dijkstra_ori(g, 1, n))


if __name__ == '__main__':
    T = 1
    # T = II()
    while T: solve(); T -= 1

堆优化版C++：

1
2
3
4
5
6
```

堆优化版Python：

```python

【最短路】Floyd求最短路

https://www.acwing.com/problem/content/856/

题意：给定一个稠密有向图，可能存在重边与自环，给出多个询问，需要给出每一个询问的两个点之前的最短路径长度

思路：我们采用动态规划的思路。在此使用多阶段决策的方法，即每一个路径状态为选择 1→k1\to k 个点的情况下的最短路径长度

  • 状态表示：f[k][i][j] 表示在前 kk 个顶点中进行选择（中转），ii 号点到 jj 号点的最短路径长度
  • 状态转移：对于第 kk 个顶点，我们可以选择中转，也可以不中转。
    • 对于不选择中转的情况：f[k][i][j] = f[k-1][i][j]
    • 对于可选择中转的情况：f[k][i][j] = f[k-1][i][k] + f[k-1][k][j]
    • 在其中取最小值即可，但是有一个注意点：对于第二种情况，选择是有一个约束的：即如果选择了 kk 号点进行转移的话，那么 ii 号点到 kk 号点以及 kk 号点到 jj 号点都是需要有路径可达的，从而可以选择最小距离
  • 初始化：即选择 0 个站点进行中转时，即 f[0][i][j] 的情况中，
    • 如果 ii 号点与 jj 号点自环，则取 00
    • 如果 ii 号点与 jj 号点之间有边，则取重边的最小值
    • 如果 ii 号点与 jj 号点之间无边，则初始化为正无穷
  • 答案状态：对于 aa 号点到 bb 号点之间的最小路径长度，就是 f[n][a][b]
  • 时间复杂度：O(n3)O(n^3)
  • 空间复杂度：O(n3)O(n^3)

空间优化推导：我们尝试优化掉记忆数组的第一维度

  • 对于不选择的情况：由于决策局面 kk 是从前往后枚举，故当前状态 f[k][i][j] 可以直接依赖于已经更新出来且不会被当前状态之后的状态再次覆盖的最优子结构 f[i][j]。即上一个局面的选择情况，就是不选择第 kk 个顶点的情况

  • 对于选择的情况：如果删除第一维度，我们担心的是当前状态 f[k][i][j] 依赖的两个状态 f[i][k] 与 f[k][j] 会不会被后续覆盖掉，即我们不确定 f[i][k] 与 f[k][j] 是否是当前第 k 个局面的最优子结构。尝试推导：

    为了确定 f[i][k] 与 f[k][j] 是否是当前第 kk 个局面的最优子结构，其实就是确定对于当前第 kk 个局面，这两个状态会不会在当前状态 f[i][j] 之后被更新覆盖，那么我们就看这两个状态是从哪里转移过来进行更新的。如果 f[i][k] 与 f[k][j] 这两个状态的转移会依赖于当前状态之后的状态，那么删除第一维度就是错误的，反之就是成立的。

    尝试推导 f[i][k] 与 f[k][j] 从何转移更新：利用我们未删除维度时正确的状态转移方程进行推演

    我们知道：f[k][i][k] = min(f[k-1][i][k], f[k-1][i][k] + f[k-1][k][k])，其中的 f[k-1][k][k] 就是一个自环的路径长度，由于 floydfloyd 算法的约束条件是没有负环，因此 f[k-1][k][k] 一定大于零，故 f[k][i][k] 一定取前者，即 f[k][i][k] = f[k-1][i][k]

    同理可知：

    f[k][k][j] = f[k-1][k][j]

    基于上述推导我们可以知道，当前第 kk 个决策局面中的 f[k][i][k] 与 f[k][k][j] 是依赖于上一个决策局面 k−1k-1 的，也就是说这两个状态一定是早于当前状态 f[i][j] 被更新覆盖的，故 f[i][k] 与 f[k][j] 就是当前第 kk 个局面的最优子结构，证毕，可以进行维度的删除

  • 时间复杂度：O(n3)O(n^3)

  • 空间复杂度：O(n2)O(n^2)

不优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, Q;
int f[N][N][N];

int main() {
    cin >> n >> m >> Q;
    
    // init
    memset(f, INF, sizeof f);
    
    // add edges and generate base
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;
        if (a == b) continue;                           // 重边就不赋值
        else if (f[0][a][b] == INF) f[0][a][b] = w;     // 第一次加边则直接赋值
        else f[0][a][b] = min(f[0][a][b], w);           // 再次赋边权就取最小值
    }
    
    // generate base again
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) 
                f[0][i][j] = 0;                         // 自环取边权为 0
    
    // dp 
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++) {
                // 不选第k个顶点
                f[k][i][j] = f[k - 1][i][j];
                
                // 选择第k个顶点
                if (f[k - 1][i][k] != INF && f[k - 1][k][j] != INF)
                    f[k][i][j] = min(f[k][i][j], f[k - 1][i][k] + f[k - 1][k][j]);
            }

    // query
    while (Q--) {
        int a, b;
        cin >> a >> b;
        if (f[n][a][b] == INF) cout << "impossible\n";
        else cout << f[n][a][b] << "\n";
    }
    
    return 0;
}

优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, Q;
int f[N][N];

int main() {
    cin >> n >> m >> Q;
    
    // init
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) f[i][j] = 0;
            else f[i][j] = INF;
            
    // base
    while (m--) {
        int a, b, w;
        cin >> a >> b >> w;
        if (a == b) continue;
        else if (f[a][b] == INF) f[a][b] = w;
        else f[a][b] = min(f[a][b], w);
    }
    
    // dp
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (f[i][k] != INF && f[k][j] != INF)
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
    
    // query
    while (Q--) {
        int a, b;
        cin >> a >> b;
        if (f[a][b] == INF) cout << "impossible\n";
        else cout << f[a][b] << "\n";
    }
    
    return 0;
}

【最短路】关闭分部的可行集合数目

https://leetcode.cn/problems/number-of-possible-sets-of-closing-branches/

标签：二进制枚举、最短路

题意：给定一个含有 nn 个顶点的无向图，如何删点可以使得剩余的图中顶点两两可达且最大距离不超过 maxDistance？返回所有删点的方案数。

思路：由于 nn 的数据范围只有 1→101 \to 10，我们可以直接枚举所有的删点方案。那么如何检查一个方案的合法性呢？直接使用最短路算法检查「所有顶点到每一个顶点」的最远距离即可。这里我们采用朴素 dijkstra 算法。

时间复杂度：O(2n×n3)O(2^n \times n^3) - 其中枚举需要 O(2n)O(2^n)、计算所有顶点到某个顶点的最远距离需要 O(n2)O(n^2)、检查所有顶点需要 O(n)O(n)

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
public:
    int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
        vector<vector<int>> g(n, vector<int>(n, INT_MAX >> 1));
        for (auto& r: roads) {
            int u = r[0], v = r[1], w = r[2];
            g[u][v] = g[v][u] = min(g[u][v], w);
        }

        auto get_max_dist = [&](int mask, int v) {
            vector<bool> SPT(n);
            vector<int> d(n, INT_MAX);
            
            d[v] = 0;
            SPT[v] = true;
            
            int cnt = 0;
            for (int i = 0; i < n; i++) {
                if (mask & (1 << i) && !SPT[i]) {
                    cnt++;
                    d[i] = min(d[i], d[v] + g[v][i]);
                }
            }

            for (int k = 1; k <= cnt - 1; k++) {
                int vex = -1;
                for (int i = 0; i < n; i++) {
                    if (mask & (1 << i) && !SPT[i] && (vex == -1 || d[i] < d[vex])) {
                        vex = i;
                    }
                }
                SPT[vex] = true;
                for (int i = 0; i < n; i++) {
                    if (mask & (1 << i) && !SPT[i]) {
                        d[i] = min(d[i], d[vex] + g[vex][i]);
                    }
                }
            }
            
            int max_dist = -1;
            for (int i = 0; i < n; i++) {
                if (mask & (1 << i)) {
                    max_dist = max(max_dist, d[i]);
                }
            }
            
            return max_dist;
        };

        int res = 0;
        for (int mask = 0; mask < 1 << n; mask++) {
            bool ok = true;
            for (int i = 0; i < n; i++) {
                if (mask & (1 << i) && get_max_dist(mask, i) > maxDistance) {
                    ok = false;
                    break;
                }
            }
            res += ok;
        }

        return res;
    }
};
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution:
    def numberOfSets(self, n: int, maxDistance: int, roads: List[List[int]]) -> int:
        g = [[10 ** 6 for _ in range(n)] for _ in range(n)]
        for u, v, w in roads:
            g[u][v] = g[v][u] = min(g[u][v], w)
        
        def get_max_dist(mask: int, v: int):
            SPT = [False for _ in range(n)]
            d = [10 ** 6 for _ in range(n)]

            SPT[v] = True
            d[v] = 0

            cnt = 0
            for i in range(n):
                if mask & (1 << i) and not SPT[i]:
                    cnt += 1
                    d[i] = min(d[i], d[v] + g[v][i])
            
            for _ in range(cnt - 1):
                vex = -1
                for i in range(n):
                    if mask & (1 << i) and not SPT[i] and (vex == -1 or d[i] < d[vex]):
                        vex = i
                SPT[vex] = True
                for i in range(n):
                    if mask & (1 << i) and not SPT[i]:
                        d[i] = min(d[i], d[vex] + g[vex][i])
                
            max_dist = -1
            for i in range(n):
                if mask & (1 << i):
                    max_dist = max(max_dist, d[i])
            
            return max_dist

        res = 0
        for mask in range(1 << n):
            ok = True
            for i in range(n):
                if mask & (1 << i) and get_max_dist(mask, i) > maxDistance:
                    ok = False
                    break
            res += ok

        return res

【思维/遍历】图的遍历

https://www.luogu.com.cn/problem/P3916

题意：给定一个有向图，求解每一个点可以到达的编号最大的点

思路：如果从正向考虑，很显然的一个暴力方法就是对于每一个点都跑一遍 dfs 或者 bfs 获取可达的最大点编号，时间复杂度 O(n2)O(n^2)，如果想要在遍历的过程中同时更新其余的点，那只有起点到最大点之间的点可以被更新，可以通过递归时记录路径点进行，时间复杂度几乎不变。我们尝试反向考虑：反向建边。既然正向考虑时需要标记的点为最大点与起点的路径，那不如直接从最大值点开始遍历搜索，在将所有的边全部反向以后，从最大值点开始遍历图，这样就可以在线性时间复杂度内解决问题

时间复杂度：O(n+m)O(n+m)

bfs 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
using namespace std;

const int N = 100010;

int n, m;
vector<int> g[N], res(N);

void bfs(int now) {
    queue<int> q;

    res[now] = now;
    q.push(now);
    
    while (q.size()) {
        int h = q.front();
        q.pop();
        for (auto& ch: g[h]) {
            if (!res[ch]) {
                res[ch] = now;
                q.push(ch);
            }
        }
    }
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        g[b].push_back(a);
    }

    for (int i = n; i >= 1; i--) {
        if (!res[i]) {
            bfs(i);
        }
    }
    
    for (int i = 1; i <= n; i++) {
        cout << res[i] << ' ';
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

dfs 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
using namespace std;

const int N = 100010;

int n, m, val;
vector<int> g[N], res(N);

void dfs(int now) {
    res[now] = val;
    for (auto& ch: g[now]) {
        if (!res[ch]) {
            dfs(ch);
        }
    }
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        g[b].push_back(a);
    }

    for (int i = n; i >= 1; i--) {
        if (!res[i]) {
            val = i;
            dfs(i);
        }
    }
    
    for (int i = 1; i <= n; i++) {
        cout << res[i] << ' ';
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

【遍历/并查集】孤立点数量

https://www.acwing.com/problem/content/5560/

题意：给定一个无向图，可能不连通，没有重边和自环。现在需要给图中的每一条无向边定向，要求所有的边定完向以后 0 入度的点尽可能的少，给出最少的 0 入度点的数量

思路：我们知道对于一棵树而言，n 个结点一共有 n-1 条边，也就可以贡献 n-1 个入度，因此至少有一个点的入度为 0。而如果不是一棵树，就会有至少 n 条边，也就至少可以贡献 n 个入度，那么 n 个结点就至少全都有入度了。显然的，一个图至少含有 n 条边时就一定有环。有了上述思路以后就可以发现，这道题本质上就是在判断连通分量是否含有环，如果有环，那么该连通分量定向边以后就不会产生 0 入度的顶点，反之，如果没有环，那么定向边以后最少产生 1 个 0 入度的点。

  • 算法一：遍历图。我们采用 dfs 遍历的方式即可解决问题。一边遍历一边打标记，遇到已经打过标记的非父结点就表明当前连通分量有环。我们使用 C++ 实现

    时间复杂度：O(n+m)O(n+m)

  • 算法二：并查集。由于没有重边，因此在判断每一个连通分量是否含有环时，可以直接通过该连通分量中点和边的数量关系得到结果。我们使用 Python 和 JavaScript 实现

    时间复杂度：O(n)O(n)

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// 实现 dfs 算法

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#include <set>
using namespace std;

const int N = 100010;

int n, m;
vector<int> G[N];
bool vis[N];

void dfs(int fa, int now, bool& hasLoop) {
    vis[now] = true;
    for (auto& ch: G[now]) {
        if (ch != fa) {
            if (vis[ch]) hasLoop = true;
            else dfs(now, ch, hasLoop);
        }
    }
}

void solve() {
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        G[b].push_back(a);
    }
    
    int res = 0;
    
    for (int i = 1; i <= n; i++) {
        if (!vis[i]) {
            bool hasLoop = false;
            dfs(-1, i, hasLoop);
            if (!hasLoop) res++;
        }
    }
    
    cout << res << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 实现 dsu 算法

p = [_ for _ in range(100010)]


def Find(x: int) -> int:
    if x != p[x]: p[x] = Find(p[x])
    return p[x]


def solve() -> None:
    n, m = map(int, input().split())

    edgeNum = [0] * (n + 1) # 每个点的连边数

    for _ in range(m):
        u, v = map(int, input().split())
        edgeNum[u] += 1
        edgeNum[v] += 1
        p[Find(u)] = Find(v)

    union = {}

    class node:
        def __init__(self):
            self.v = self.e = 0

    for i in range(1, n + 1):
        nowp = Find(i)
        if nowp not in union: union[nowp] = node()

        union[nowp].v += 1
        union[nowp].e += edgeNum[i]

    res = 0

    for comp in union:
        if union[comp].e >> 1 == union[comp].v - 1:
            res += 1

    print(res)


if __name__ == "__main__":
    solve()

JavaScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// 实现 dsu 算法

const readline = require('readline');
const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout,
});

let n = null;
let m = null;
let p = [], edgeNum = [];

rl.on('line', line => {
    const [a, b] = line.split(' ').map(i => Number(i));
    if (n === null) {
        n = a;
        m = b;
        for (let i = 1; i <= n; i++) {
            p[i] = i;
            edgeNum[i] = 0;
        }
    } else {
        edgeNum[a]++;
        edgeNum[b]++;
        p[Find(a)] = Find(b);
    }
});

rl.on('close', () => {
    const res = solve();
    console.log(res);
});

function Find(x) {
    if (x != p[x]) p[x] = Find(p[x]);
    return p[x];
}

function solve() {
    let res = 0;

    // 自定义结构体
    class Node {
        constructor() {
            this.v = 0;
            this.e = 0;
        }
    }

    /*
        另一种结构体定义方法
        function Node() {
            this.v = 0;
            this.e = 0;
        }
    */

    // 哈希
    let union = new Map();

    for (let i = 1; i <= n; i++) {
        let nowp = Find(i); // 当前结点的祖宗结点 nowp
        if (!union.has(nowp)) union.set(nowp, new Node());

        union.get(nowp).v += 1;
        union.get(nowp).e += edgeNum[i];
    }

    // 判断
    for (let i of union.keys()) {
        if (union.get(i).e >> 1 === union.get(i).v - 1) {
            res++;
        }
    }

    return res;
}

【LCA】树的直径

https://www.acwing.com/problem/content/5563/

题意：给定一棵树，初始时含有 4 个结点分别为 1 到 4，其中 1 号为根结点，2 到 4 均为根结点的叶子结点。现在进行 Q 次操作，每次指定一个已经存在的结点向其插入两个新结点作为叶节点。现在需要在每次操作以后输出这棵树的直径。我们定义树的直径为：树中距离最远的两个点之间的距离。

思路一：暴力搜索。

  • 我们将树重构为无向图，对于每一个状态的无向图，首先从任意一个已存在的结点 A 开始搜索到距离他最远的点 B，然后从 B 点出发搜索到离他最远的点 C，则 B 与 C 之间的距离就是当前状态的树的直径。由于每一个状态的树都要遍历两遍树，于是时间复杂度就是平方阶

  • 时间复杂度：O(qn)O(qn)

思路二：最近公共祖先 LCA。

  • 从树的直径出发。我们知道，树的直径由直径的两个结点之间的距离决定，因此我们着眼于这两个结点 AA 和 BB 展开。不妨设当前局面直径的两个结点已知为 AA 和 BB，现在插入两个叶子结点 L1L_1 和 L2L_2。是否改变了树的直径大小取决于新插入的两个结点对于当前树的影响情况。如果 L1L_1 或 L2L_2 可以替代 AA 或 BB，则树的直径就会改变。很显然新插入的两个叶子结点对于直径的两个端点影响是同效果的，因此我们统称新插入的叶子结点为 LL。

  • 什么时候树的直径会改变？对于 AA、BB 和 LL 来说，直径是否改变取决于 LL 能否替代 AA 或 BB，一共有六种情况。我们记 dist(A,L)=da\text{dist}(A,L)=da，dist(B,L)=db\text{dist}(B,L)=db，当前树的直径为 resres，六种情况如下：

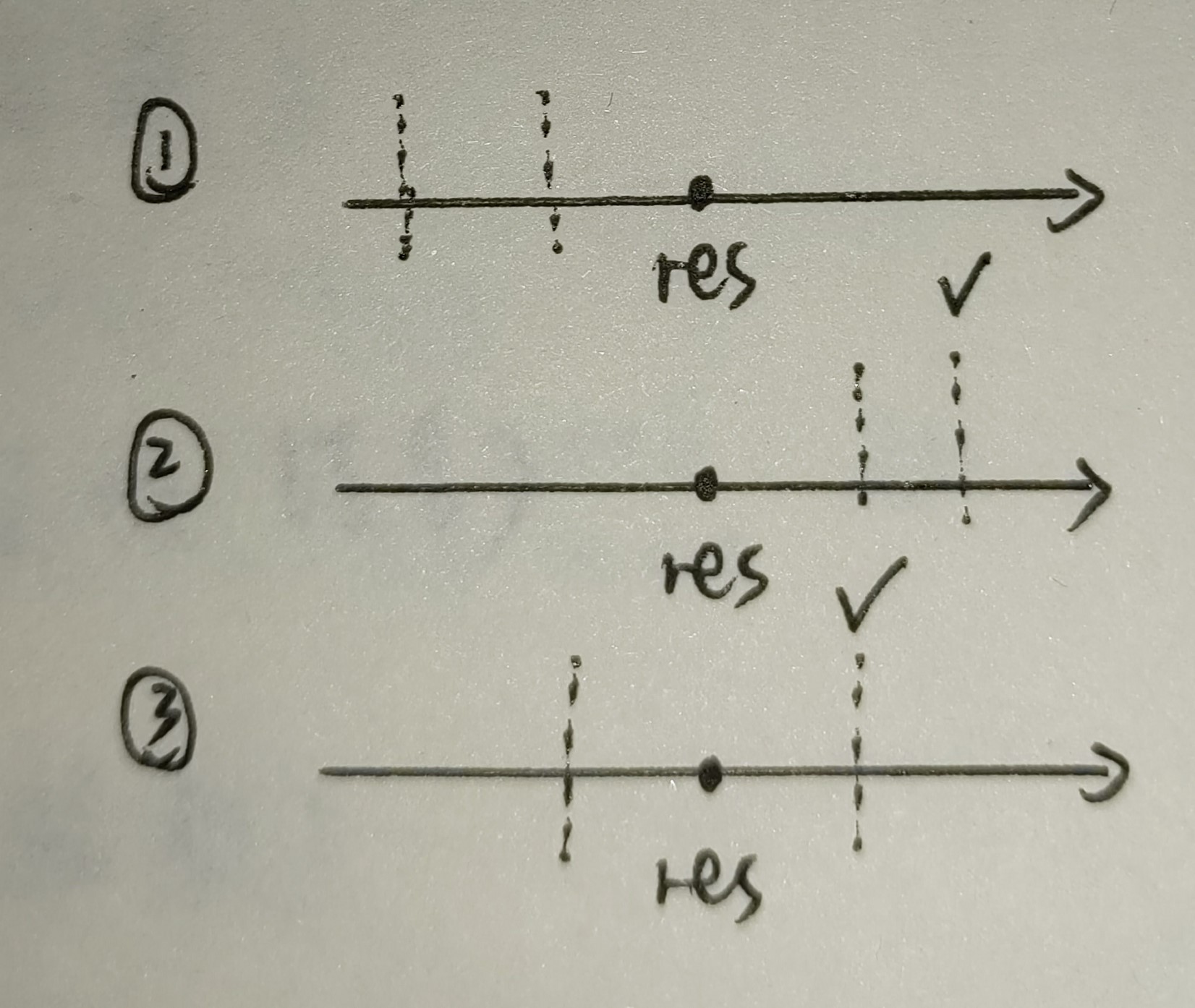
    1. max(da,db)≤res\text{max}(da, db) \le \text{res}，交换 AA 和 BB 得到 22 种
    2. min(da,db)≥res\text{min}(da,db) \ge \text{res}，交换 AA 和 BB 得到 22 种
    3. max(da,db)>res,min(da,db)<res\text{max}(da,db) >res,\text{min}(da,db) < \text{res}，交换 AA 和 BB 得到 22​ 种

    如图：我们只需要在其中的最大值严格超过当前树的直径 res\text{res} 时更新直径对应的结点以及直径的长度即可

    六种情况

  • 如何快速计算树上任意两个点之间的距离？我们可以使用最近公共祖先 LCA 算法。则树上任意两点 x,yx,y 之间的距离 dist(x,y)\text{dist}(x,y) 为：

    dist(x,y)=dist(x,root)+dist(y,root)−2×dist(lca(x,y),root)\text{dist}(x,y) = \text{dist}(x,root) + \text{dist}(y,root) - 2 \times \text{dist}(\text{lca}(x,y),root)

  • 时间复杂度：O(qlog⁡n)O(q \log n)

暴力搜索代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#include <set>
using namespace std;

const int N = 500010;

vector<int> g[N];
int d[N];
bool vis[N];
pair<int, int> res;     // first 为最远距离；second 为对应结点编号

void dfs(int pre, int now) {
    if (vis[now]) return;
    
    vis[now] = true;
    
    if (pre != -1) {
        d[now] = d[pre] + 1;
        if (d[now] > res.first) {
            res = {d[now], now};
        }
    }
    
    for (auto& ch: g[now]) {
        dfs(now, ch);
    }
}

void solve() {
    // init
    for (int i = 2; i <= 4; i++) {
        g[1].push_back(i);
        g[i].push_back(1);
    }
    
    int now = 4;
    
    int Q;
    cin >> Q;
    while (Q--) {
        int id;
        cin >> id;
        
        g[id].push_back(++now);
        g[now].push_back(id);
        
        g[id].push_back(++now);
        g[now].push_back(id);
        
        res = {-1, -1};
        
        // 第一趟
        memset(vis, false, sizeof vis);
        memset(d, 0, sizeof d);
        d[1] = 0;
        dfs(-1, 1);
        
        // 第二趟
        memset(vis, false, sizeof vis);
        memset(d, 0, sizeof d);
        d[res.second] = 0;
        dfs(-1, res.second);
        
        cout << res.first << "\n";
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}

LCA 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#include <set>
using namespace std;

const int N = 1000010, M = 20;

int d[N];        // d[i] 表示 i 号点到根结点的距离
int to[N][M];    // to[i][j] 表示 i 号点向上跳 2^j 步后到达的结点编号

int lca(int a, int b) {
    if (d[a] < d[b]) swap(a, b);

    for (int k = M - 1; k >= 0; k--)
        if (d[to[a][k]] >= d[b])
            a = to[a][k];

    if (a == b) return a;

    for (int k = M - 1; k >= 0; k--)
        if (to[a][k] != to[b][k])
            a = to[a][k], b = to[b][k];

    return to[a][0];
}

int dist(int a, int b) {
    return d[a] + d[b] - 2 * d[lca(a, b)];
}

void solve() {
    int Q;
    cin >> Q;

    // init lca
    for (int i = 2; i <= 4; i++) {
        d[i] = 1;
        to[i][0] = 1;
    }

    int A = 2, B = 4, now = 4, res = 2;

    while (Q--) {
        int fa;
        cin >> fa;

        int L1 = ++now, L2 = ++now;

        // upd lca
        d[L1] = d[fa] + 1;
        d[L2] = d[fa] + 1;
        to[L1][0] = fa;
        to[L2][0] = fa;
        for (int k = 1; k <= M - 1; k++) {
            to[L1][k] = to[ to[L1][k-1] ][ k-1 ];
            to[L2][k] = to[ to[L2][k-1] ][ k-1 ];
        }

        int da = dist(A, L1), db = dist(B, L1);

        if (max(da, db) <= res) res = res;
        else if (min(da, db) >= res) {
            if (da > db) res = da, B = L1;
            else res = db, A = L1;
        } else {
            if (da > db) res = da, B = L1;
            else res = db, A = L1;
        }

        cout << res << "\n";
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
//    cin >> T;
    while (T--) solve();
    return 0;
}
Algorithm
graphs
https://blog.dwj601.cn/Algorithm/graphs/
作者
Mr_Dwj
发布于
2024年3月21日
更新于
2024年7月25日
许可协议