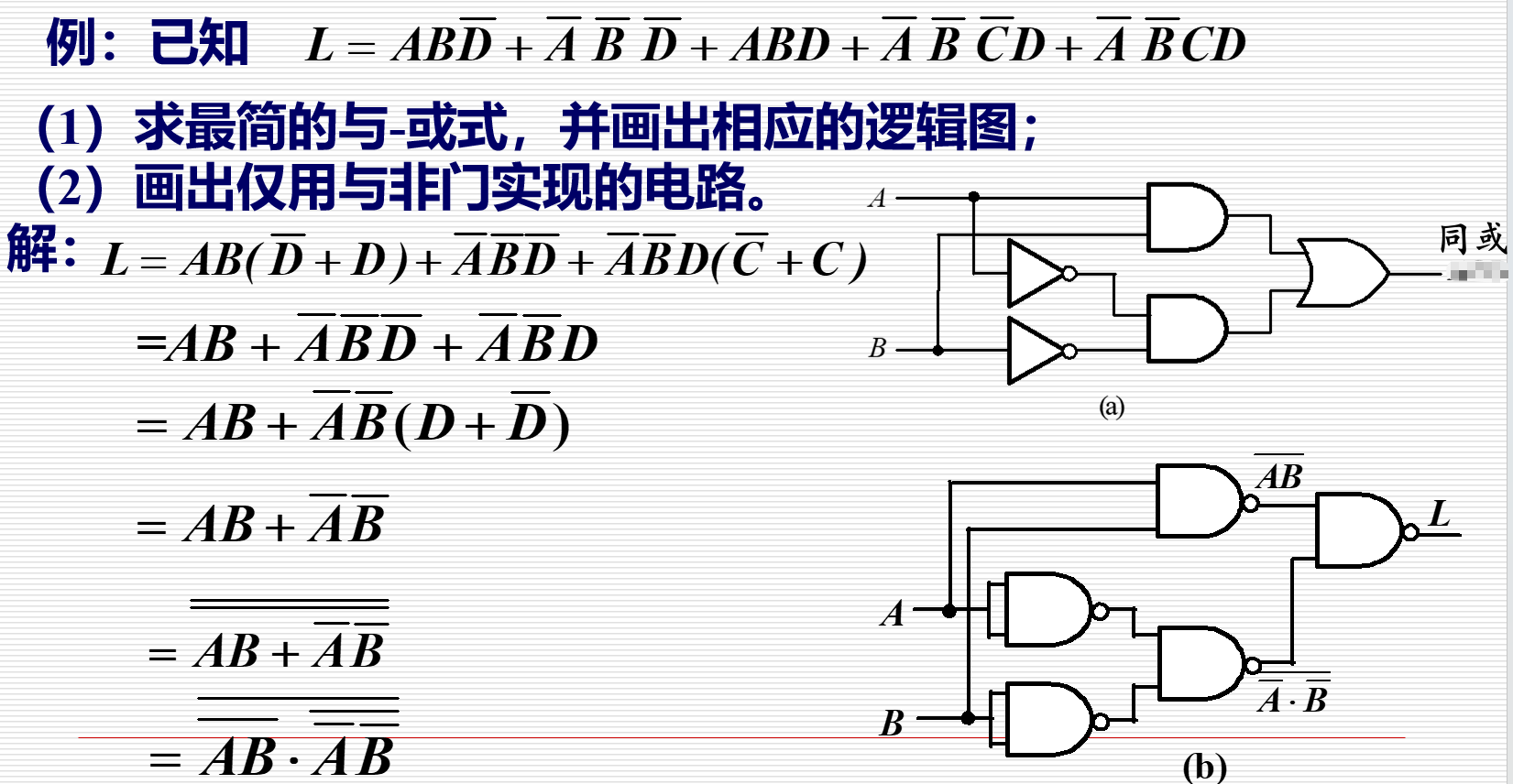
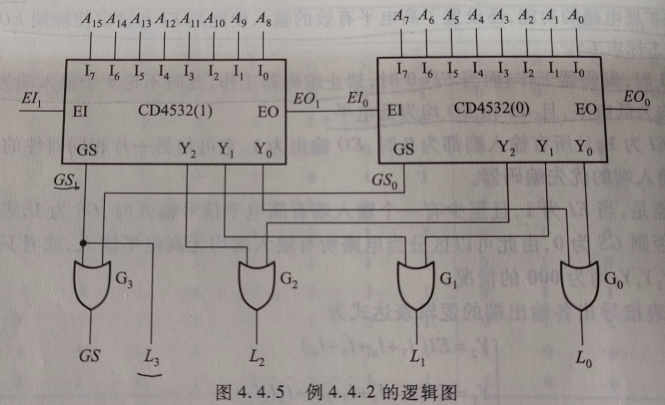
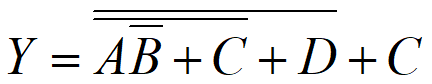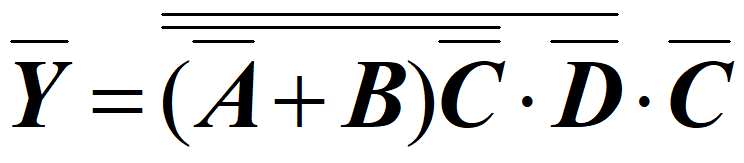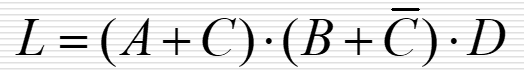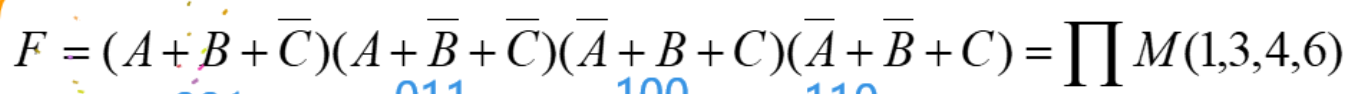数字逻辑电路
1 概论¶
从结构特点及其对输入信号的响应规则角度可以将数字集成电路分为「组合逻辑电路」和「时序逻辑电路」两种。
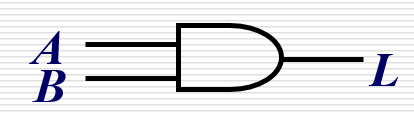
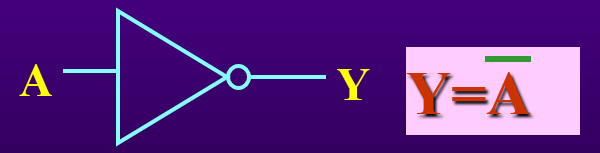
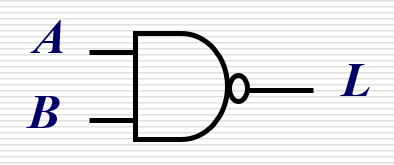
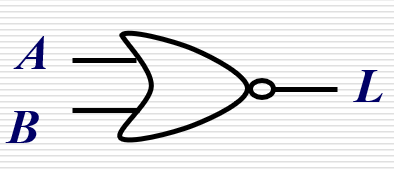
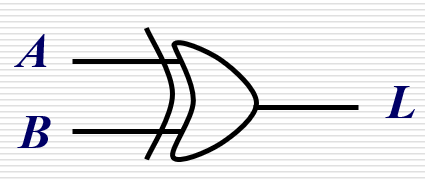
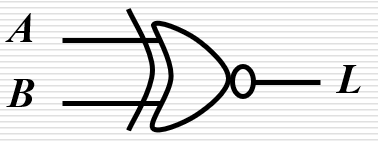
常见逻辑符号表:
使用逻辑函数表示实际问题:
| 实际问题 | 图片示例 | 变量表示 | 列真值表 | 逻辑函数 |
|---|---|---|---|---|
 |
 |
 |
 |
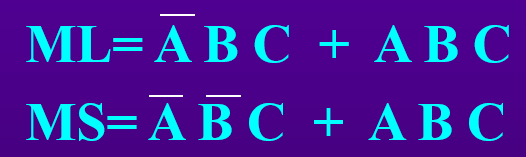 |
逻辑函数1及其表示方法
| 方法 | 示例 |
|---|---|
| 真值表 |  |
| 逻辑函数表达式 | 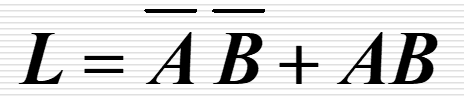 |
| 逻辑图 |  |
| 波形图 | 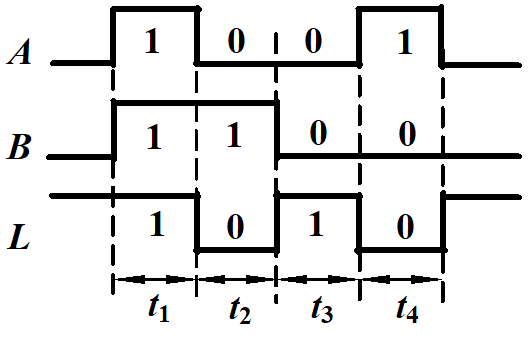 |
真值表到逻辑图的转换:
逻辑图到真值表的转换:
2 逻辑代数 | 硬件描述语言基础¶
2.1 基本定律和规则¶
2.1.1 基本定律和恒等式¶
2.1.2 基本规则¶
-
代入规则 - 类似于换元
-
反演规则(获得反函数 \(\overline Y\) )
觉得烦可以直接进行取反运算,简单明了不会错
- 对于任意一个逻辑表达式 L,与门 & 或门取反,变量取反,0 & 1 取反
- 保持原来的运算优先顺序(即如果在原函数表达式中,AB 之间先运算,再和其他变量进行运算,那么非函数的表达式中,仍然是 AB 之间先运算)
- 对于反变量以外的非号应保留不变
-
对偶规则(获得对偶式 \(L'\) )
- 对于任何逻辑函数式:与门、或门取反,0、1 取反
2.2 逻辑函数表达式的形式¶
2.2.1 基本形式¶
2.2.2 最小项与最小项表达式¶
2.2.3 最大项与最大项表达式¶
2.2.4 最大项和最小项的关系¶
2.3 逻辑函数的代数化简法¶
为什么要学化简?因为化简之后可以减少门的使用,从而增强电路可靠性、降低成本
2.3.1 逻辑函数的最简形式¶
最简与或表达式:包含的与项数最少,且每个与项中变量数最少的与或表达式
2.3.2 逻辑函数的代数化简法¶
-
逻辑函数的 化简
方法 逻辑函数 证明 并项法 \(A+\overline A = 1\) 显然 吸收法 \(A+AB = A\) 提取公因子 消去法 \(A+\overline A B = A+B\) 摩根定律使用两次 配项法 \(A = A(B + \overline B)\) 显然 -
逻辑函数形式的 变换
使用场景:通常在一片集成电路芯片中只有一种门电路,为了减少门电路的种类,需要对逻辑函数表达式进行变换
变换方法:常常使用两次取反的套路进行变换
2.4 逻辑函数的卡诺图化简法¶
2.4.1 用卡诺图表示逻辑函数¶
首先写出逻辑函数的表达式并且转化为最小项表达式,最后将最小项填入相应的矩阵中即可
2.4.2 用卡诺图化简逻辑函数¶
尽可能使得圈出来的 \(2^k\) 圈中包含的数尽可能的多,即让 \(k\) 尽可能的大。注意:圈中的数全部都得是最小项的数
2.5 Verilog HDL 基础¶
为了从软件代码的角度描述电路,从下面三个方面介绍如何用 Verilog 描述数字逻辑电路。
2.5.1 门级描述¶
门级元件中,第一个位置是输出变量,之后的都是输入变量,可解释为:多输入门
| 门级元件 | 元件符号 |
|---|---|
| 与 | and |
| 或 | or |
| 非 | not |
| 与非 | nand |
| 或非 | nor |
| 异或 | xor |
| 同或 | xnor |
2.5.2 数据流描述¶
简单的概括就是使用相关的位运算进行表述,因为电路逻辑本就是二元逻辑,因此位运算就刚好匹配。在使用数据流进行电路描述时,采用的语句都是连续赋值语句,由 assign 关键词开始,多条 assign 语句是 并行 运行的
需要注意的是,在连续赋值语句中,被赋值的变量一定是 wire 的 线网 类型的变量,示例如下
2.5.3 行为描述¶
简单的概括就是使用底层语言进行编程,类似于最开始的 C 语言。使用行为描述语句进行描述时,使用 always 关键字开始变量赋值逻辑,多条 always 语句是 串行 运行的
需要注意的是,在行为描述语句中,被赋值的变量一定是 reg 等 寄存器 类型的变量,这与上述数据流描述的方式不同,示例如下
3 逻辑门电路¶
3.1 简介¶
MOS 管含有 NMOS 管和 PMOS 管,NMOS 管与 PMOS 管的组合称为互补 MOS,或称为 CMOS 电路。
3.2 基本 CMOS 逻辑门电路¶
附上启蒙的博客:MOS 管及简单 CMOS 逻辑门电路原理图解析!
| 器件 | 电路 |
|---|---|
| 开关 |  |
| 反相器(非门) | 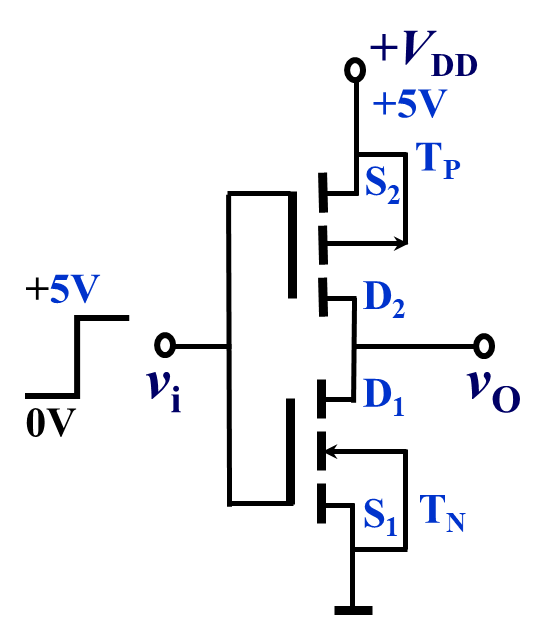 |
| 与非门 |  |
| 或非门 | 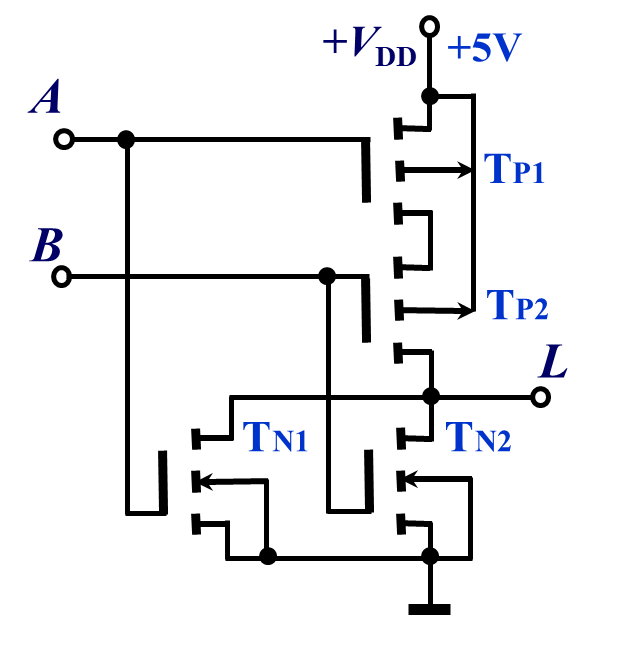 |
| 传输门(开关) | 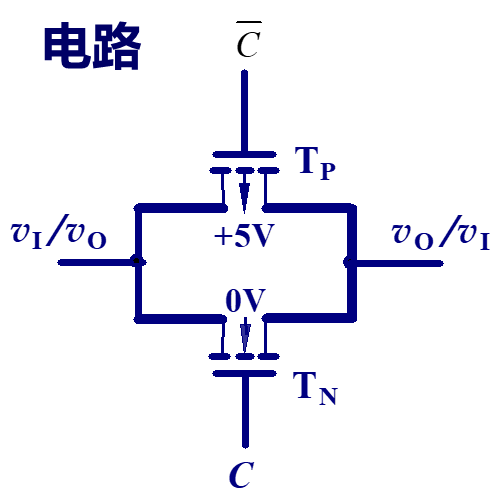 |
| 与门 |  |
| 或门 |  |
应用示例
解读的逻辑其实很简单,在理解之前,应该首先观看上面给出的连接中的 MOS 电路的简化版,从而理解电路的正确结构!即,每一个 MOS 管都理解为一个开关,何时闭合与断开完全取决于相应的 MOS 管的种类与电平,如果是 NMOS 管,即箭头指向左边的,为高电平导通,PMOS 管则相反,只需要知道此电路基本逻辑,那么接下来的分析结果就是水到渠成的事。
需要知道一个理念就是,两个电路如果是并联的存在,那么逻辑表达式就是或,简称为 并联相或;对应的,两个电路如果是串联的存在,那么逻辑表达式就是与,简称为 串联相与。最后需要补充一点的就是关于取反的辨识,我们知道一个反相器 MOS 管的逻辑是非常简单的,就是一个 NMOS 管和一个 PMOS 管的组合,那么只需要在分析多个线路是串联还是并联的关系之后,最后经过一个反相器就是一个 取反 逻辑。
| 电路 | 逻辑表达式 | 功能描述 |
|---|---|---|
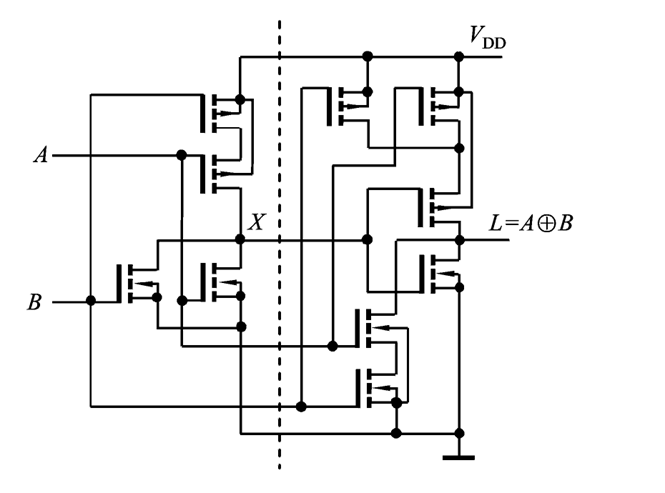 |
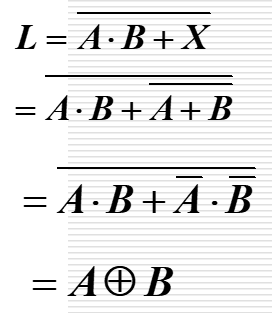 |
异或门 |
 |
\(L=\overline{(BC+D)A}\) | |
 |
\(L=\overline{(A+B)X}=\overline{(A+B)\overline{AB}}=A\odot B\) | 同或门 |
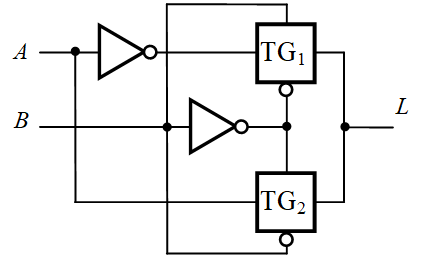 |
 |
异或门 |
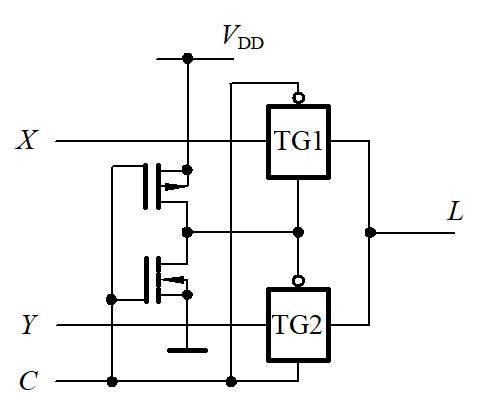 |
 |
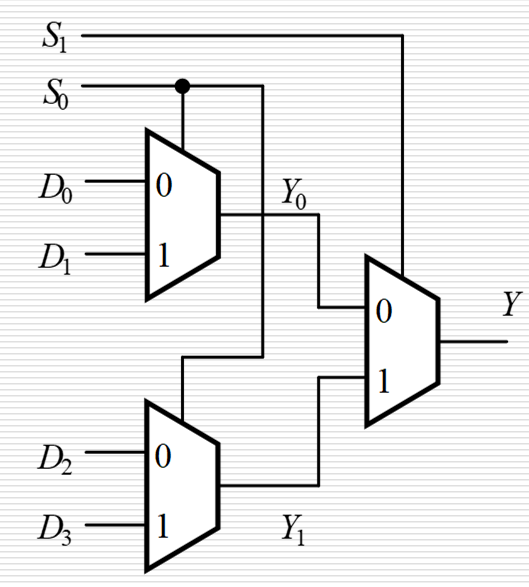
2 选 1 数据选择器 |
4 组合逻辑电路¶
4.1 分析策略¶
组合逻辑电路只取决于实时输入从而给出相应的输出,与之前的运行结果无关。没有反馈和记忆单元。分析流程如下:
- 由逻辑图得到 逻辑表达式
- 化简和变换
- 列 真值表
- 根据真值表(或者波形图)分析电路功能
4.2 设计方法¶
4.2.1 设计过程¶
- 明确逻辑含义:确定输入输出并定义逻辑状态的含义
- 列出真值表:根据逻辑描述写出真值表
- 写出逻辑表达式:由真值表写出逻辑表达式,真值取原、假值取反
- 化简逻辑表达式:代数化简法 or 卡诺图化简法
- 画出逻辑图:使用相应的门级元件进行组合连接
4.2.2 优化实现¶
| 电路类型 | 优化策略 | 电路图 | 优化结果 |
|---|---|---|---|
| 单输出电路 | 统一元件类型 | 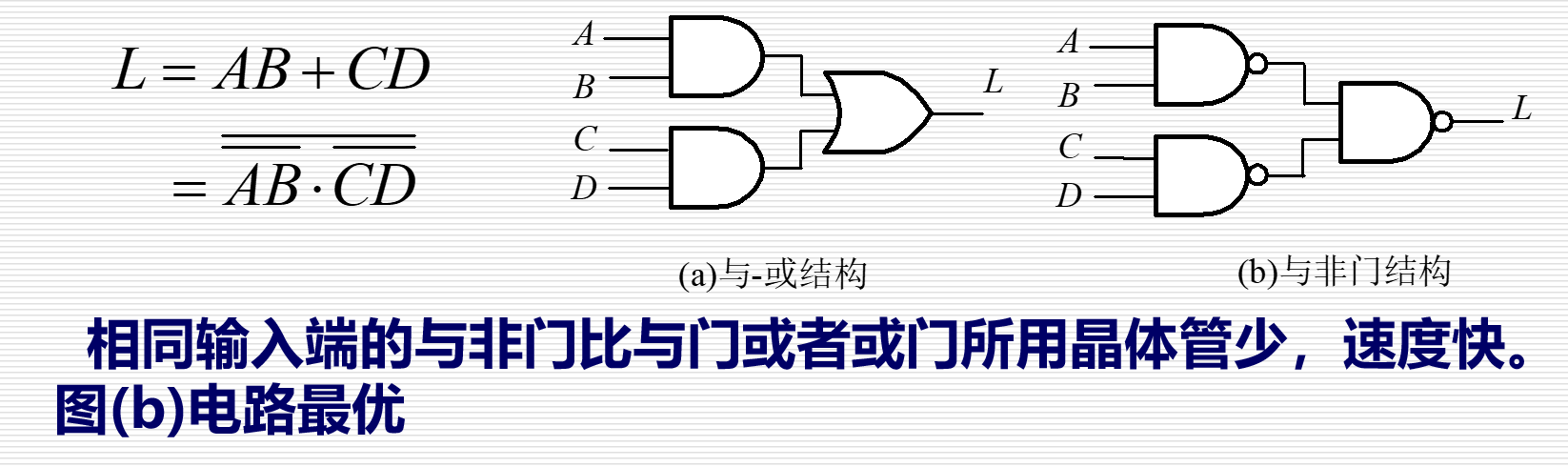 |
见左图文字 |
| 多输出电路 | 共享相同逻辑项 | 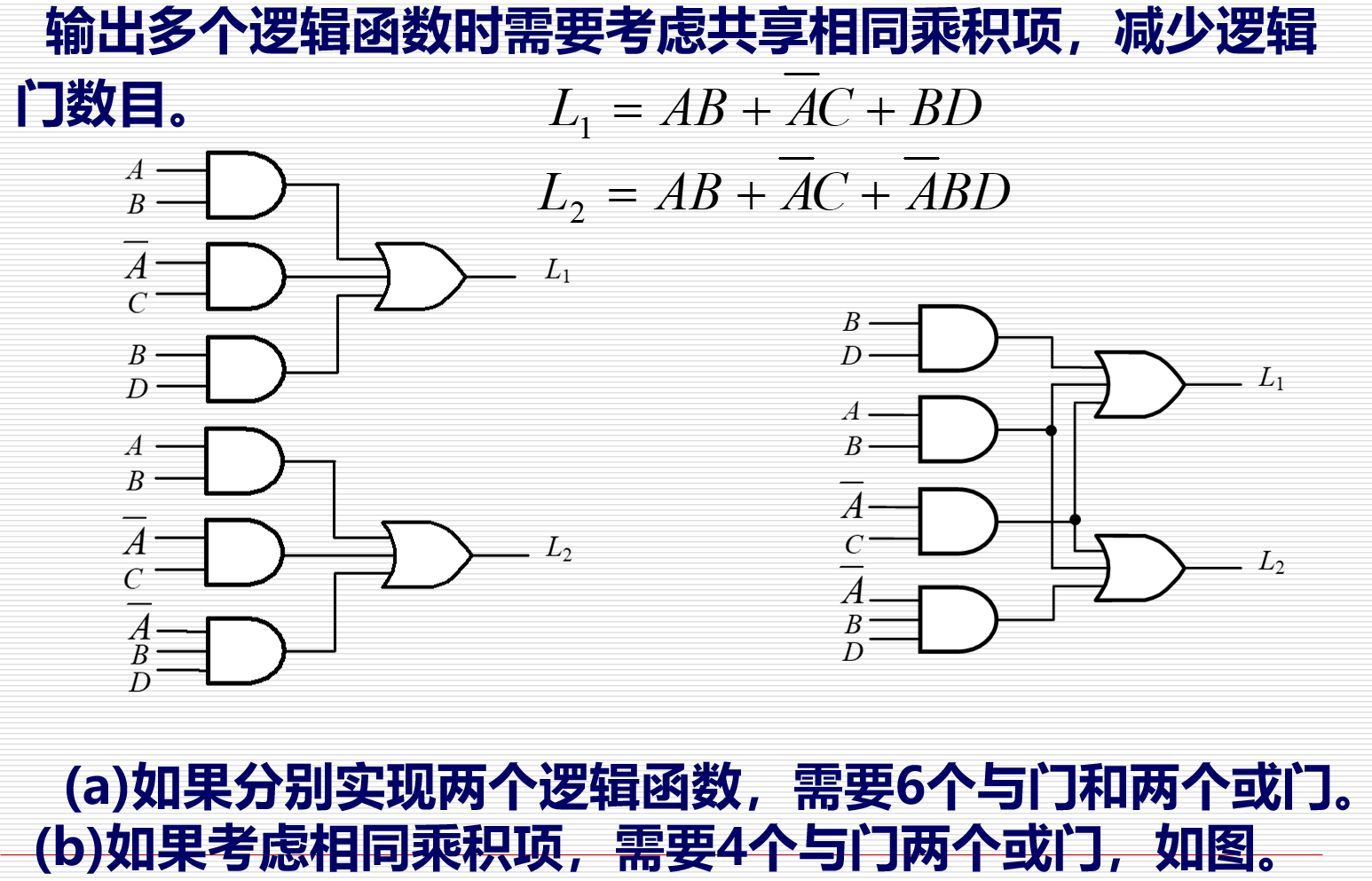 |
见左图文字 |
| 多级逻辑电路(限定入数) | 提取公因项 | 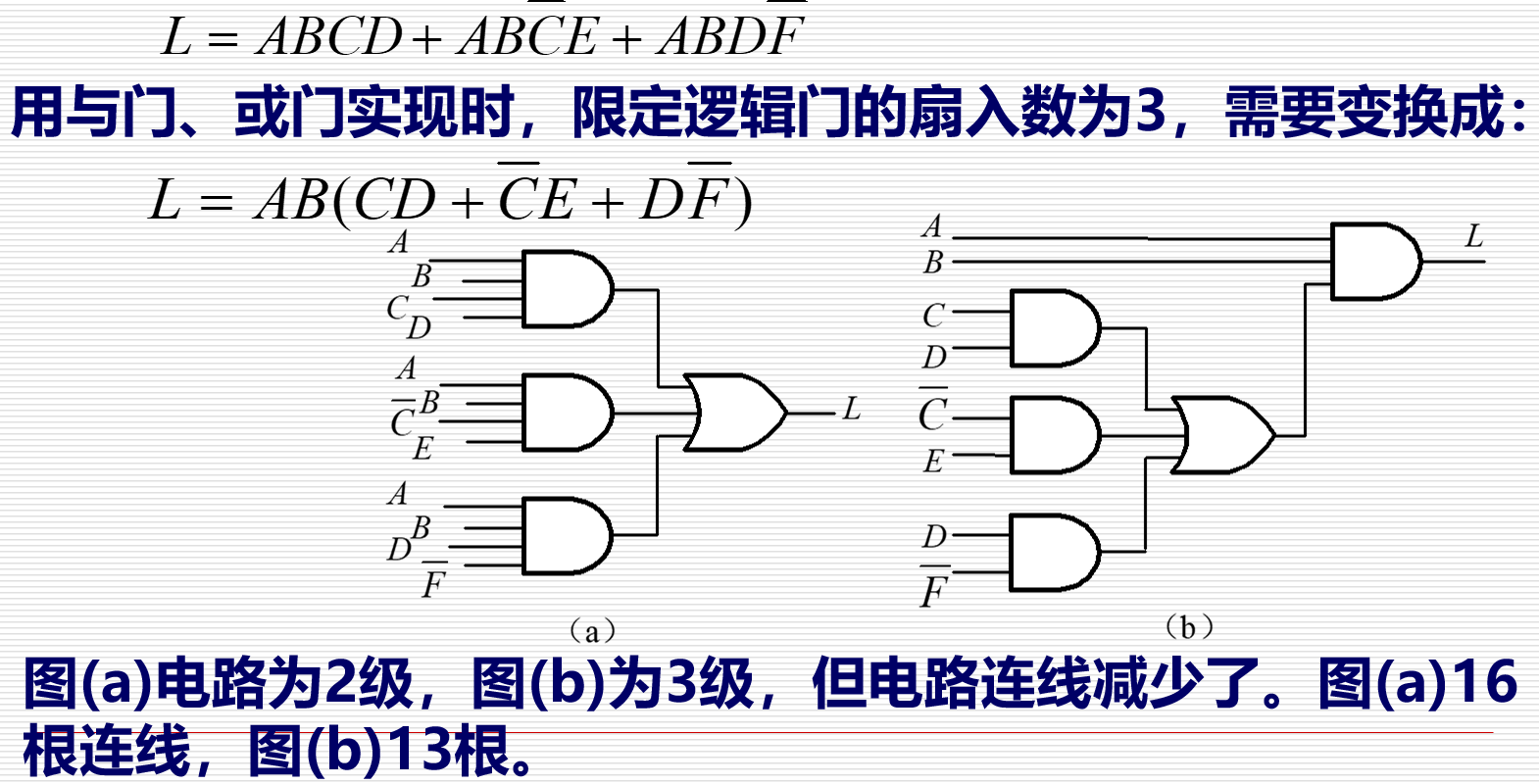 |
见左图文字 |
| 多级逻辑电路(限定入数) | 提取公因项 |  |
见左图文字 |
4.3 竞争与冒险¶
为什么会产生?门级元件的延时效应。
如何消去呢?有三种方法:
-
消除互补变量。
-
增加乘积项,避免互补项相加。
-
输出端并联电容器。如下图:
4.4 典型电路示例¶
举几个典型的组合逻辑电路。
4.4.1 编码器¶
普通编码器:只允许有一个输入,从而进行编码,一旦出现多输入就会发生错误。
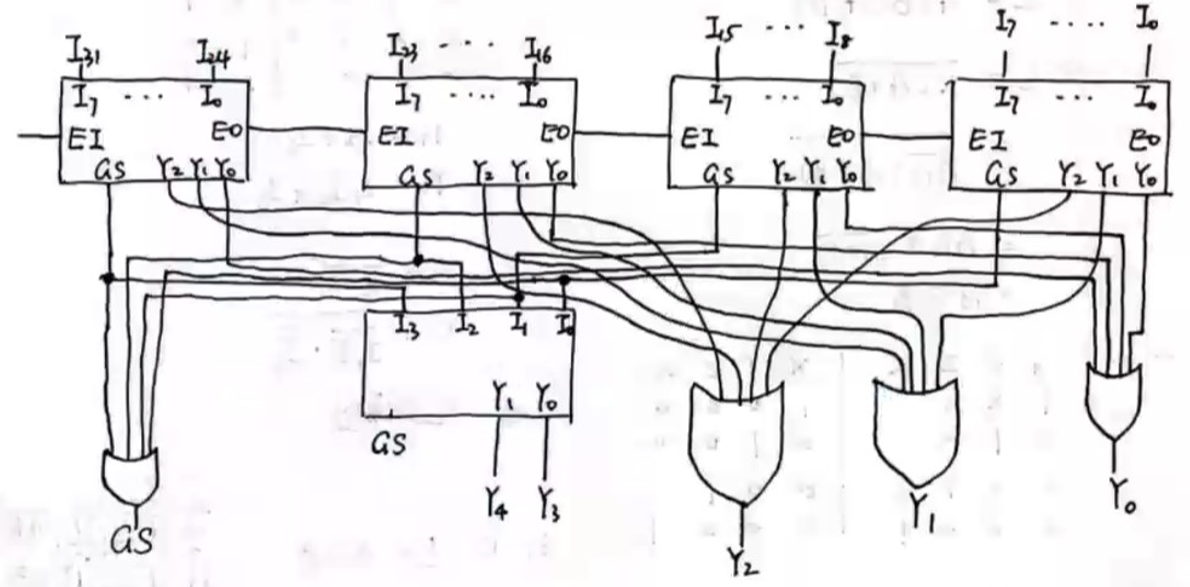
优先编码器:无论多少输入,都会按照一开始设定的优先级进行最高等级的那一个信号位的编码。
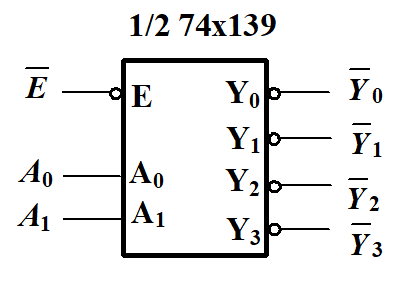
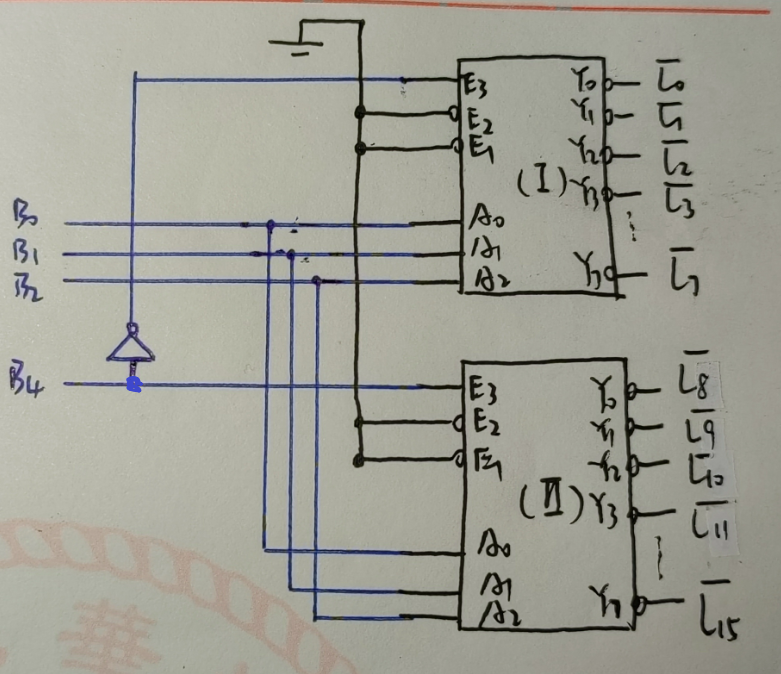
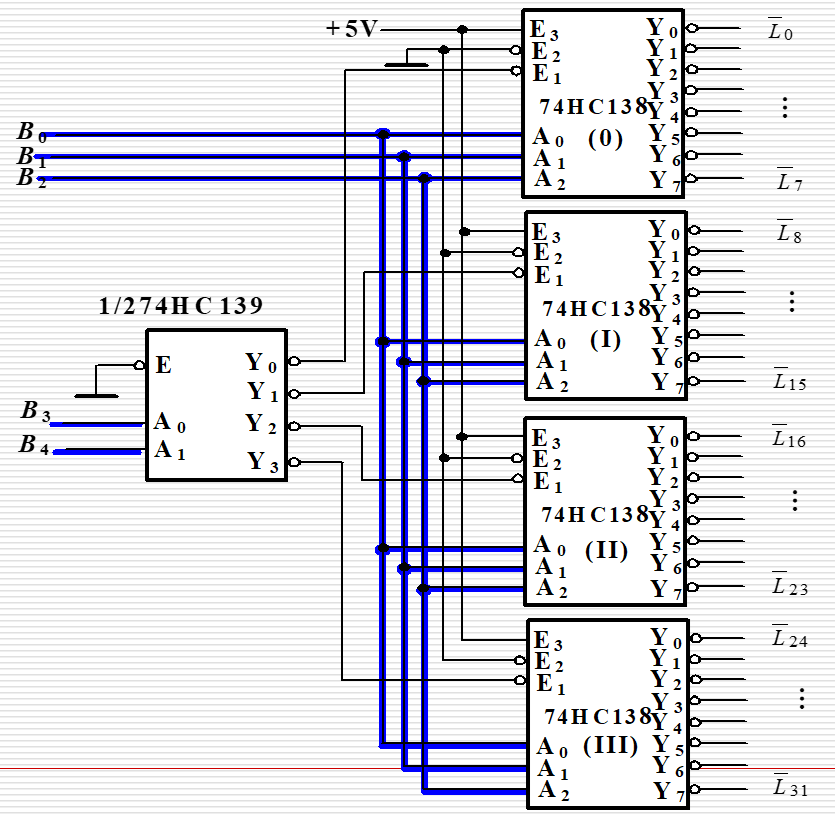
4.4.2 译码器/数据分配器¶
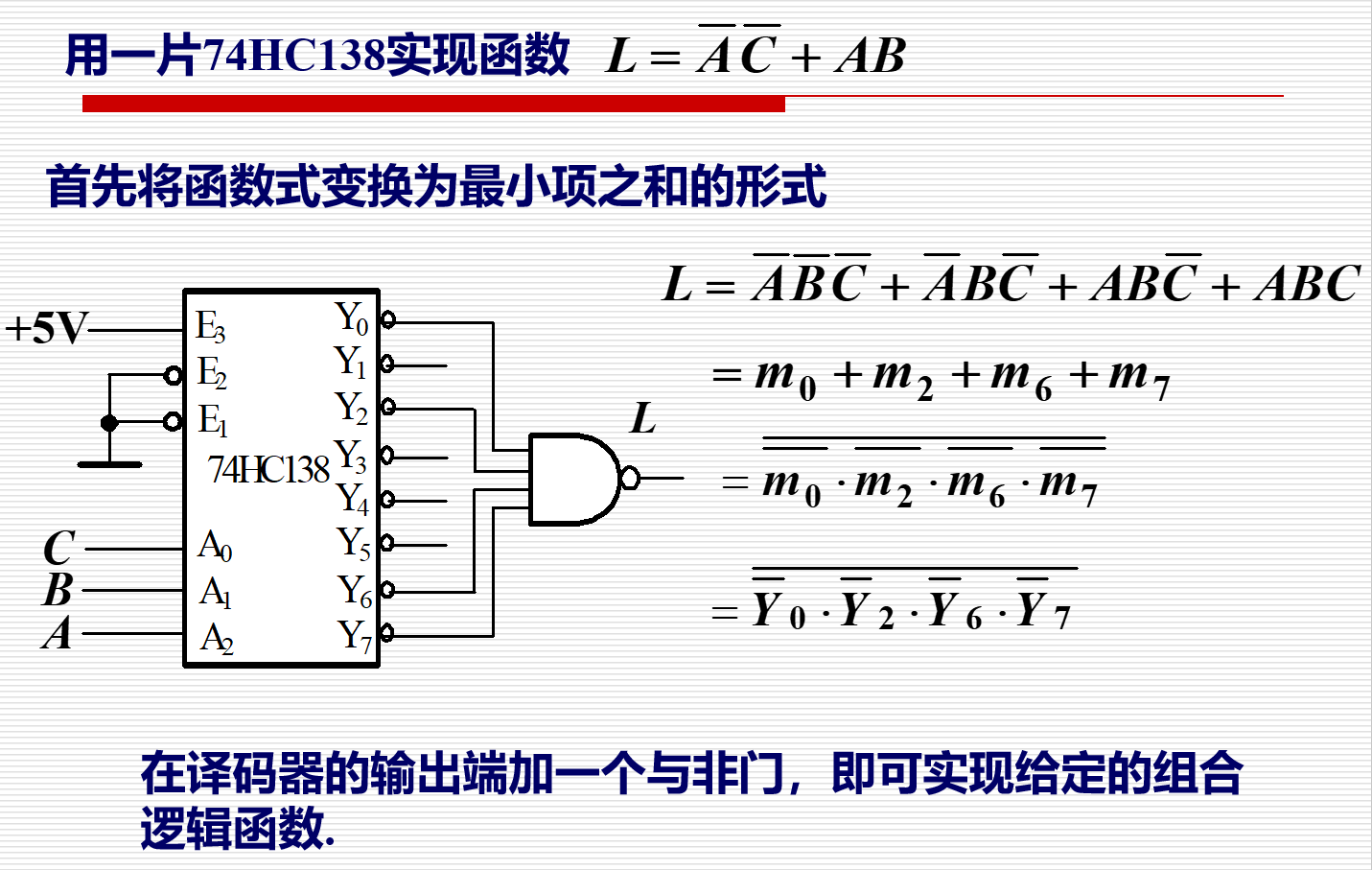
使用译码器实现逻辑函数
我们知道译码器的每一个输出代表一个最小项,那么对于一个 \(x\) 变量的逻辑函数,可以通过以下步骤用 \(x-2^x\) 译码器实现任意 \(x\) 变量的逻辑函数
- 将逻辑函数转化为最小项表达式(大量使用摩根定律)
- 转化为译码器的输出(写成 \(\sum m_i\) 的形式)
- 在译码器的输出端加一个多输入与非门即可(对结果进行与非)
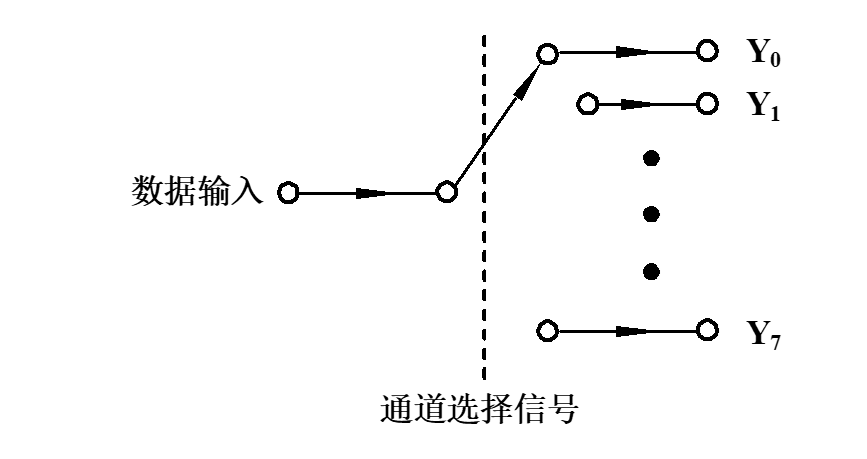
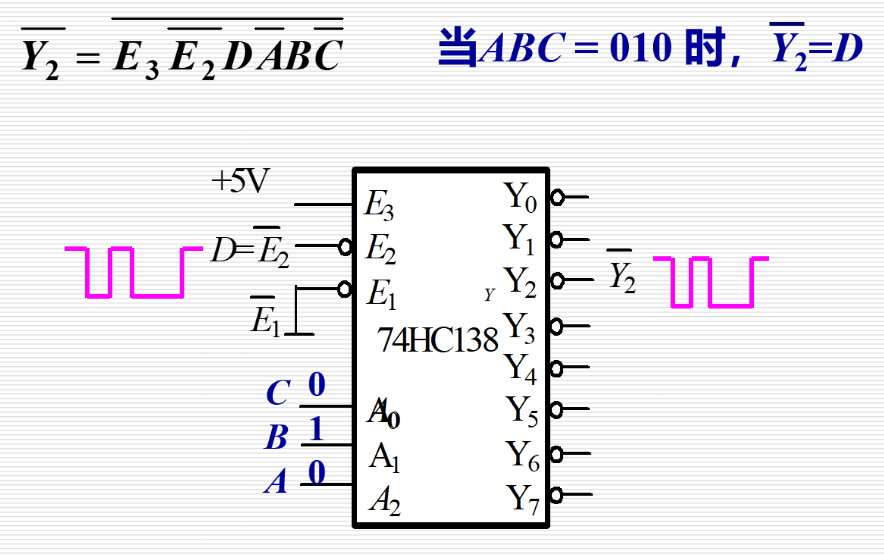
数据分配器
功能:相当于多输出的单刀多掷开关,是将公共数据线上的数据按需要送到不同的通道上去的逻辑电路。
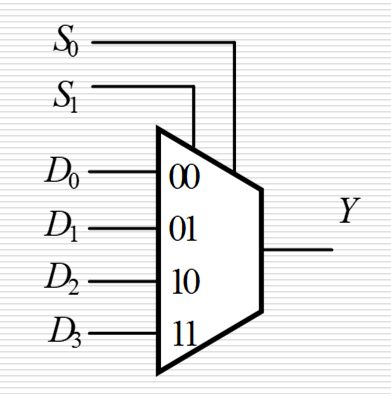
4.4.3 数据选择器¶
使用数据选择器实现逻辑函数
- 变量个数 \(<\) 数据选择端个数:变量直接对应数据选择端,多余的选择端置 0,最后相应的信号输入端进行赋 1 或赋 0 的操作即可
- 变量个数 \(=\) 数据选择端个数:本质上就是将逻辑函数转化为最小项表达式,然后与标准与或式进行比对,已出现的最小项与 1,未出现的最小项与 0,从而配凑产生了数据选择器最开始的式子。落到逻辑图上就是,数据选择端接入函数变量,信号输入端接入相应的高低电平,出现的最小项就输入 1,未出现的就输入 0 即可
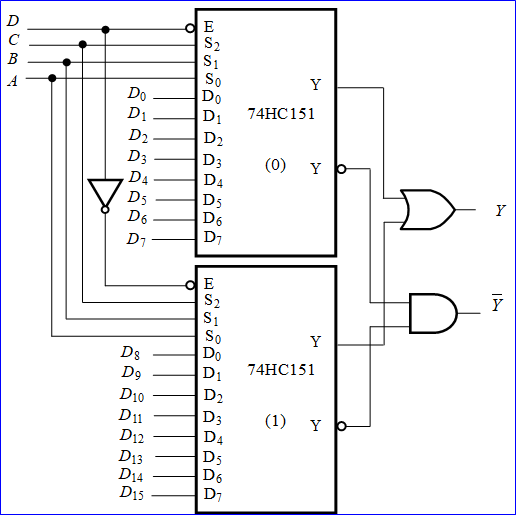
- 变量个数 \(>\) 数据选择端个数:
- 刚好多 1 个:变量 or 变量的非接入信号输入端
- 不止多 1 个:同样采用将变量作为数据信号输入端,此外可能需要借助相关的门电路辅助进行
4.4.4 数值比较器¶
略
4.4.5 算术运算电路¶
半加器:即不考虑低位进位的一位二进制加法器。其中 \(S\) 为输出位,\(C\) 为进位,没有考虑低位的进位
全加器:即考虑低位进位的一位二进制加法器。其中 \(S\) 为输出位,\(C_i\) 为低位的进位,\(C_o\) 为进位
5 锁存器和触发器¶
本章介绍时序逻辑电路的存储单元,分别为锁存器和触发器。其中锁存器对电平敏感,触发器对边沿敏感
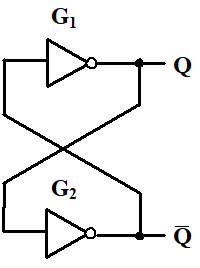
5.1 基本双稳态电路¶
5.2 SR 锁存器¶
| 门级元件组成 | 电路图 | 功能分析 |
|---|---|---|
| 或非门实现 |  |
高电平有效。全 0 不变,谁 1 谁有效,都 1 不确定状态 |
| 与非门实现 | 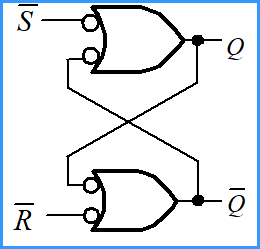 |
低电平有效。全 1 不变,谁 0 谁有效,都 0 不确定状态 |
| 应用 | 电路图 | 功能分析 |
|---|---|---|
| 开关电路 | 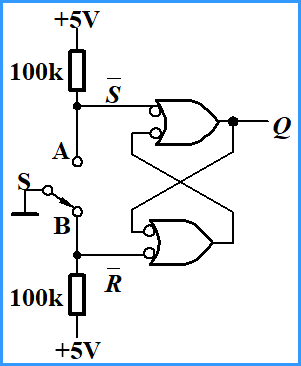 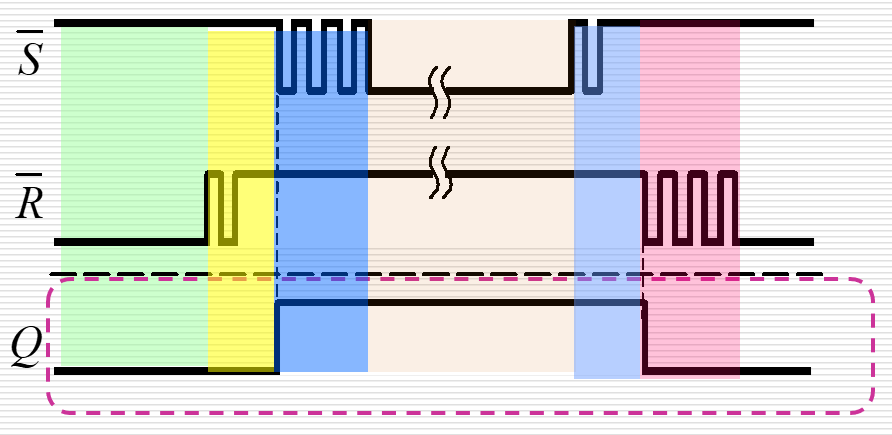 |
无论开关如何震动,输出始终正常 |
| 门控 SR 锁存器 |  |
就是加了一个使能端 E,如果 E 为 1,则就是一个基本的 SR 锁存器,如果 E 为 0,则保持 |
5.3 D 锁存器¶
| 电路名称 | 逻辑电路图 | 功能分析 |
|---|---|---|
| 传输门控制的 D 锁存器 |  |
E = 0, Q = 不变;E = 1, Q = D |
| 逻辑门控制的 D 锁存器 | 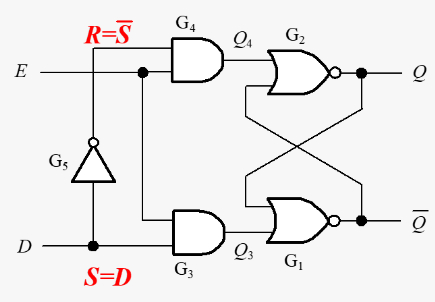 |
E = 0, Q = 不变;E = 1, Q = D |
5.4 触发器¶
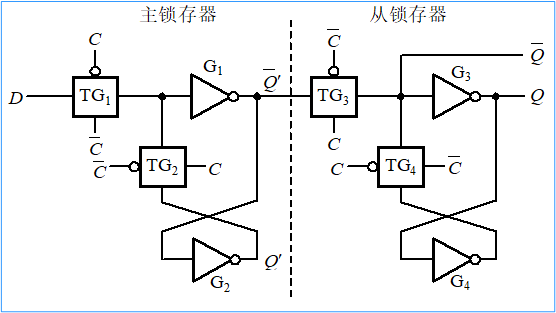
5.4.1 主从 D 触发器的电路结构和工作原理¶
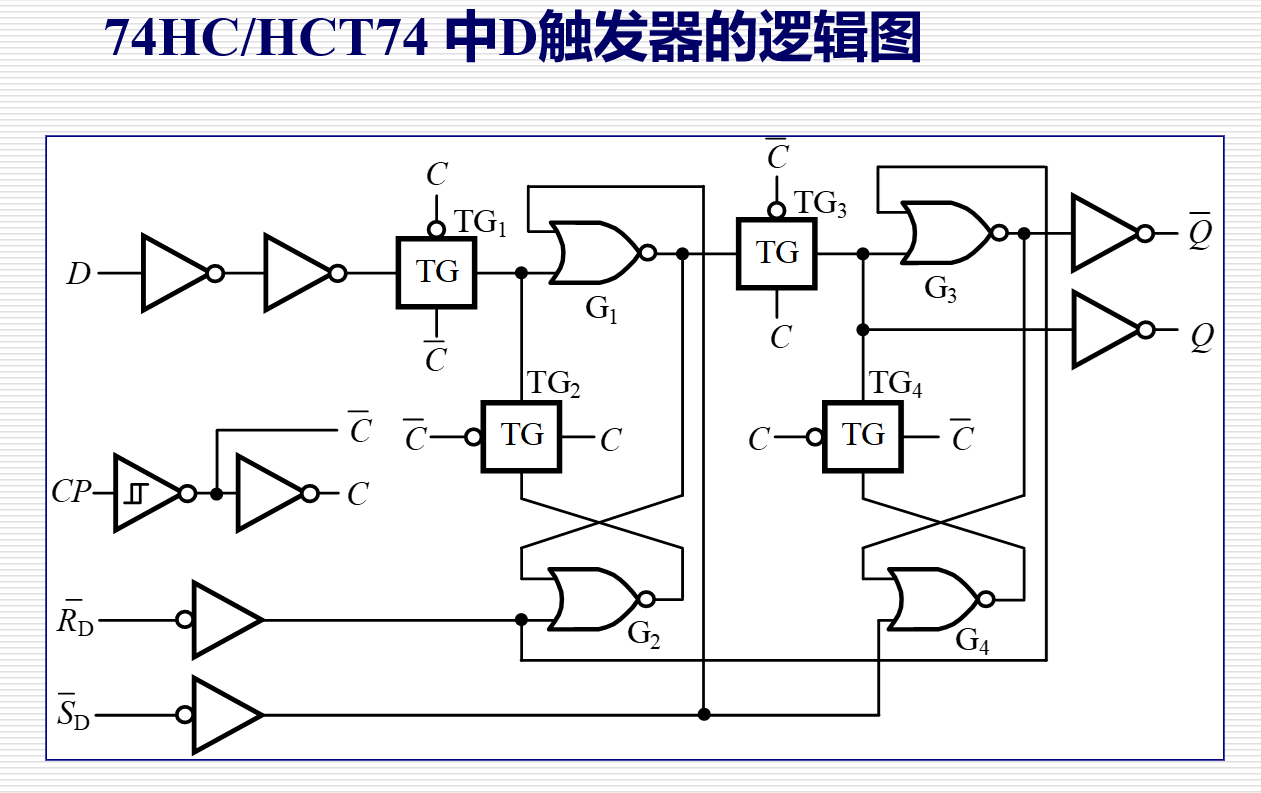
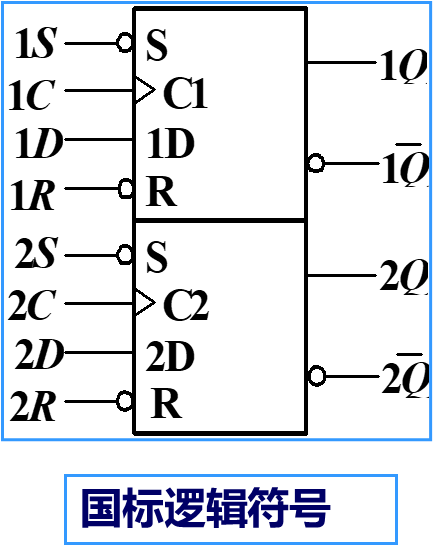
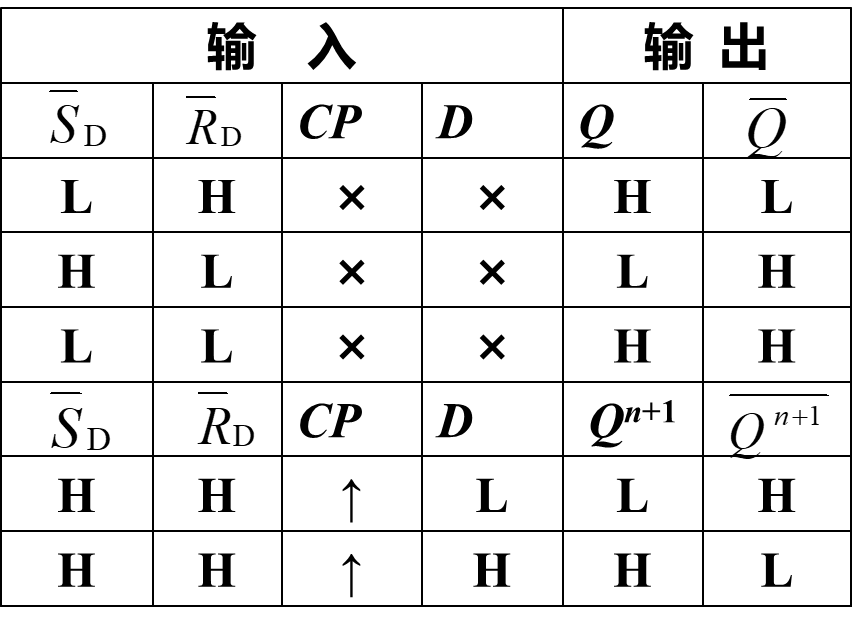
5.4.2 典型的主从 D 触发器集成电路¶
5.5 触发器的逻辑功能¶
本目需要掌握有关触发器的 特性表、特性方程、状态图 三者的单独书写以及相互转化的逻辑过程,还需要掌握不同的触发器之间的相互 替换实现
| 类型 | 逻辑符号 | 特性表 | 特性方程 | 状态图 |
|---|---|---|---|---|
| D 触发器 |  |
 |
 |
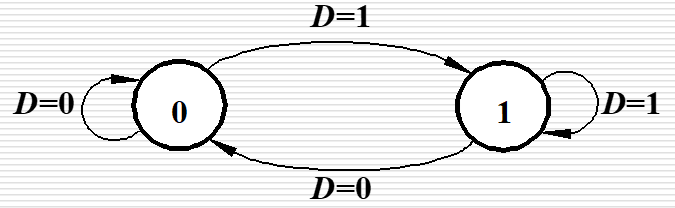 |
| JK 触发器 |  |
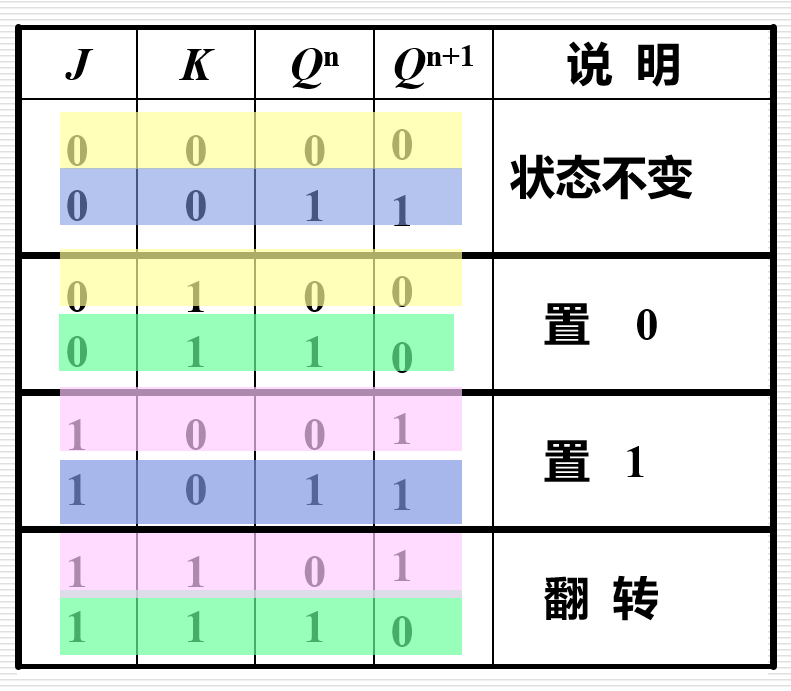 |
 |
 |
| T 触发器 |  |
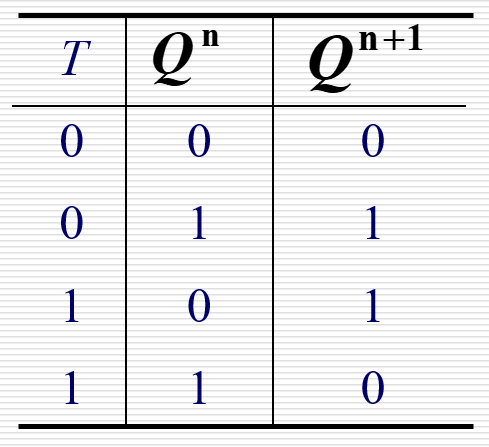 |
 |
 |
| T' 触发器 | 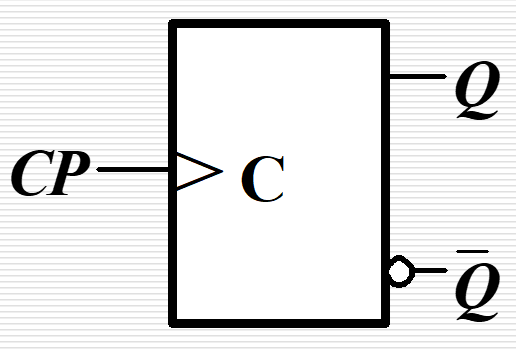 |
\(T\equiv 1\) | 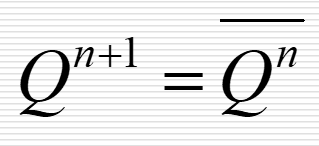 |
|
| SR 触发器 |  |
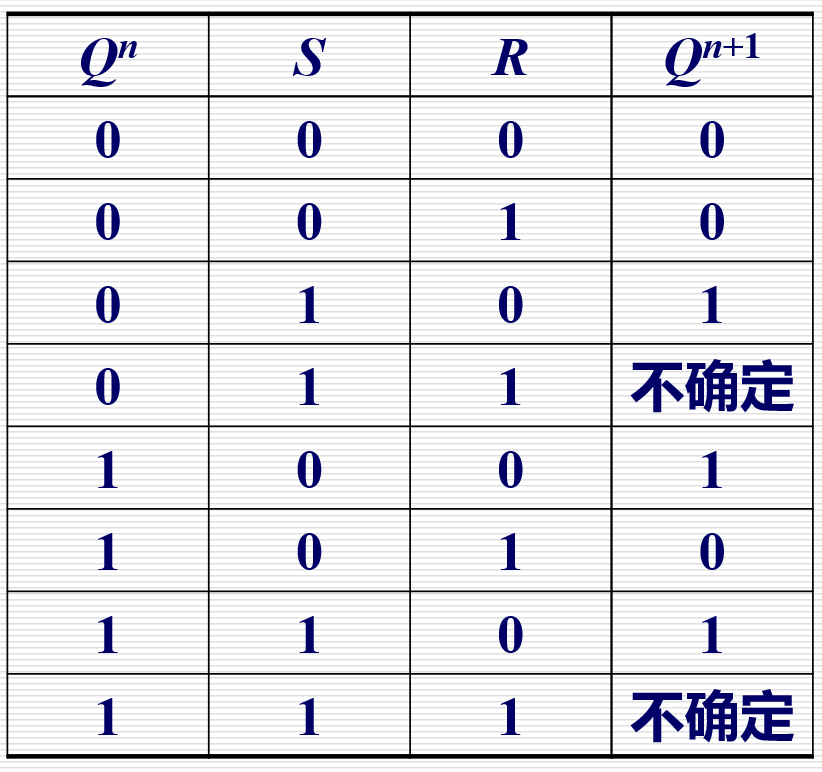 |
 |
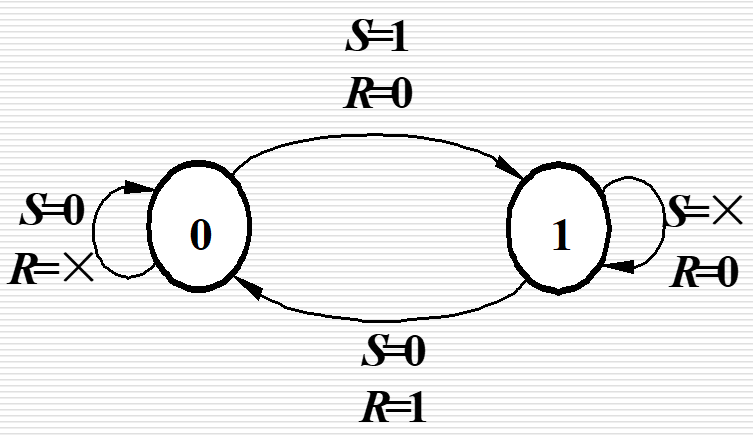 |
6 时序逻辑电路¶
本部分只需要掌握同步时序逻辑电路的分析即可,具体直接从例题出发。三道同步时序逻辑电路分析的例题见教材 P282 ~ P286,分别为:
- 例一:可控二进制计数器
- 例二:可控双向二进制计数器
- 例三:脉冲分配器
6.1 同步时序逻辑电路的分析¶
下面介绍同步时序逻辑电路分析的五个步骤。在分析之前我们要知道我们的最终目标是什么,可以知道,我们分析电路的最终目标是想要量化的确定电路的物理实现的功能,至于如何设计,此处不予讨论。现在给定了一个同步时序逻辑电路的 逻辑电路图,接下来我们应该:
-
了解电路组成:同步 or 异步?穆尔型输出(与输入无关) or 米利型输出(与输入有关) or 都有?由什么触发器组成的?触发器类型是上升沿出发 or 下降沿触发?
-
列出三个方程:
-
输出方程:电路的最终输出
-
激励方程:触发器的输入
-
状态方程:触发器的输出(将触发器的输入也就是激励方程代入触发器的特性方程即可)
-
-
写出转换表(分析功能用)
-
写出状态图(分析功能用)
-
写出时序图(分析功能用)默认状态的初值设置为 0
6.2 计数器¶
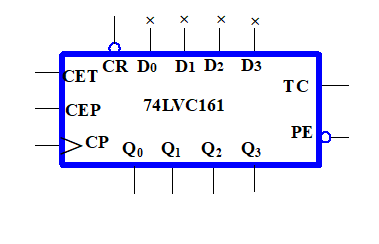
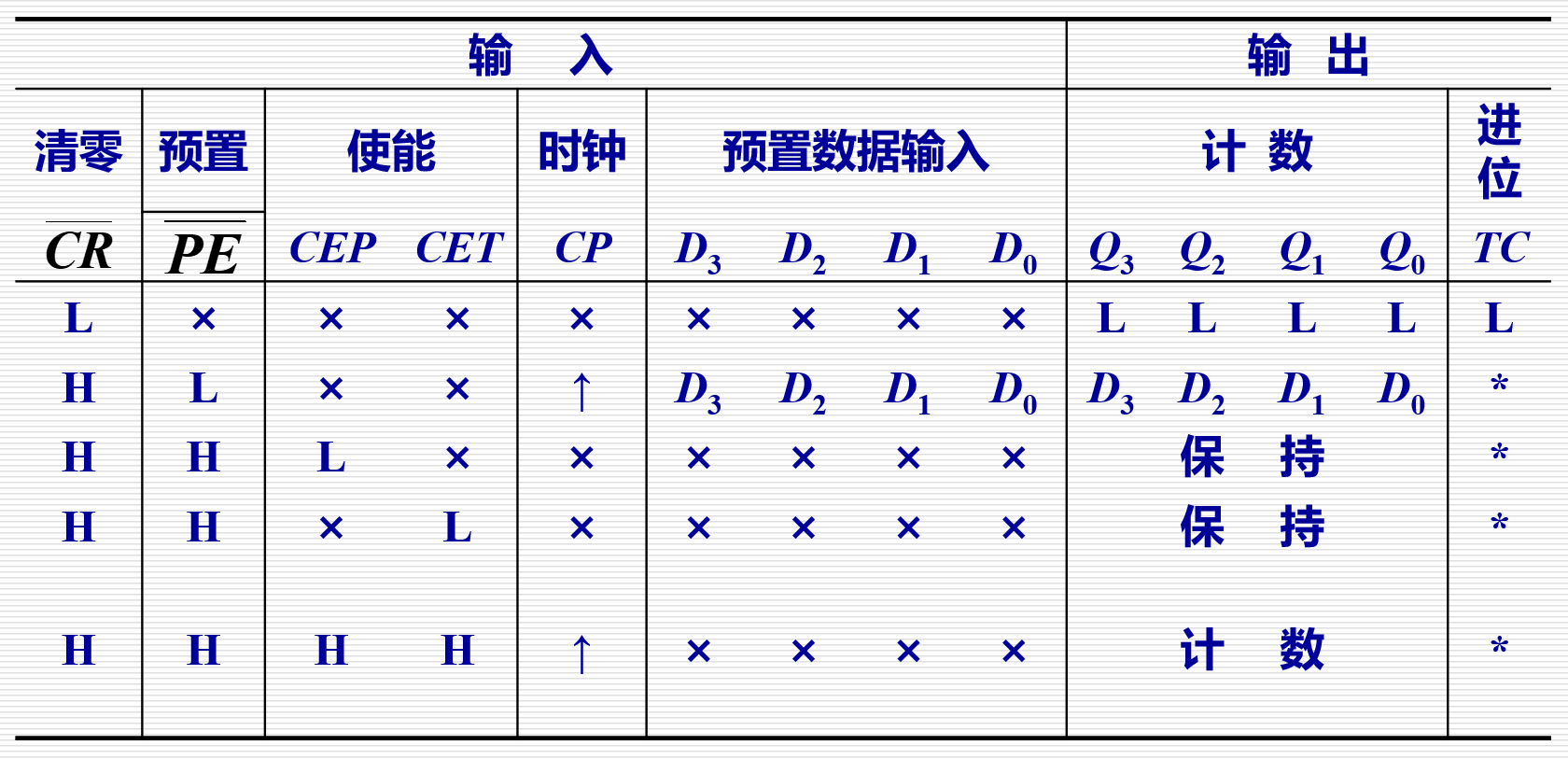
本节讲讲 N 位二进制计数器中,利用集成电路板 \(74LVC161\) 实现的 4 位同步二进制递增计数器。进而引出利用该 4 位计数器 实现模 N 计数器 的分析与设计思路。同时补充 \(74LVC162\) 实现的 4 位同步十进制递增计时器,进而引出相关的模 N 设计思路。下面分析 74LVC161 4 位同步二进制递增计数器集成板
注解:
- \(\overline{CR}\):异步清零。即无视时钟脉冲信号,直接清零
- \(\overline{PE}\):同步预置。即当有效始终脉冲沿到来时,实现 4 个预置位的输出,即 \(D_3,D_2,D_1,D_0\)
- \(CEP,CET\):使能端。同时为高电平电路才能正常工作
- \(TC\):进位输出
小结:
-
多个集成板进行计数
-
考虑如何通信:低位进位作为高位使能?
-
考虑如何清零:同步(异步)清零?同步(异步)置数?
-
学会利用 74LVC161 的“反馈清零法”实现模 N 计数器
-
学会利用 74LVC161 的”反馈置数法“实现模 N 计数器
-
学会实现 74LVC162 十进制递增功能功能(同步清零、同步置数)
-
学会利用 74LVC162 的同步清零的特性实现模 9 的九进制计数器功能
-
学会利用 74LVC162 实现模 24 的二十四进制计数器功能:
00-09 与 10-19 的计数:通过低位片的进位端,作为高位片的使能端即可
20-23 与 23-00 的计数:通过将低位片的两个低位与高位片通过 4023 三输入与非门连接起来,当全为 1 时,就是计数到 23 的状态,此时对高低片进行同步清零即可
-
描述输入逻辑变量和输出逻辑变量之间的因果关系,称为逻辑函数。 ↩