SysBasic

本文最后更新于 2024年11月14日上午

计算机系统基础

前言

学科地位：

主讲教师	学分配额	学科类别
闫文珠	3.5	专业课

成绩组成：

实验（9 次）	平时作业	期末（闭卷）
20%	30%	50%

教材情况：

课程名称	选用教材	版次	作者	出版社	ISBN 号
计算机系统基础	《计算机系统基础》	4	袁春风	机械工业出版社	978-7-111-60489-1

1 计算机系统概述

计算机基本工作原理是什么？

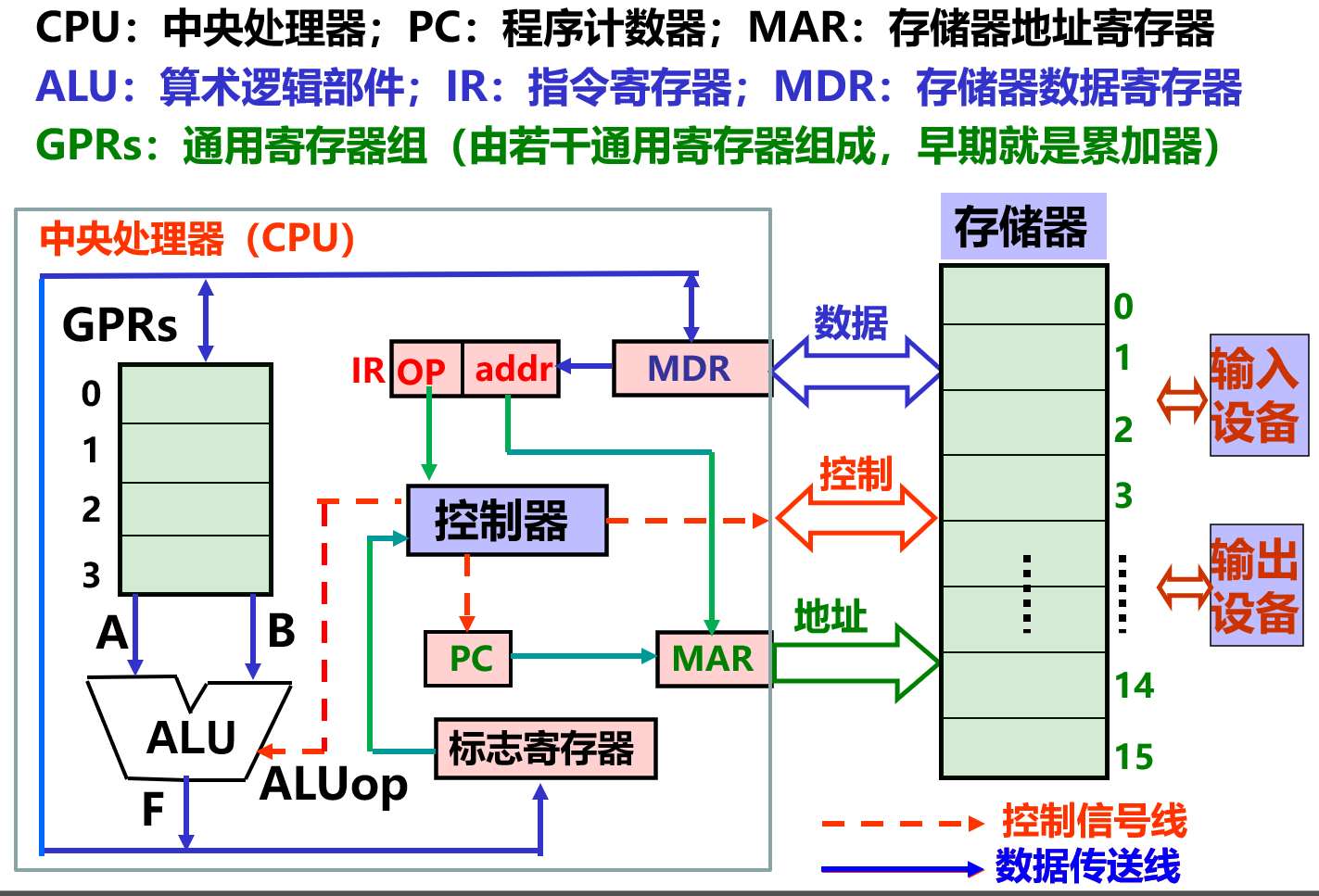
曾经。冯诺依曼认为计算机应该由五个部分组成，相互协作完成任务：1）存储器。存储数据和指令；2）运算器。可以进行四则运算和逻辑运算；3）控制器。自动取指令来执行；4）输入设备。用户输入；5）输出设备。系统输出。如下图所示：

冯.诺依曼结构 - 计算机模型

现在。计算机结构模型是这样的：

现代计算机结构模型

计算机系统的层次结构是什么？

计算机系统的层次结构

如何评价计算机系统的性能？一个完整的计算机系统由软件和硬件共同组成，而硬件的性能对其起决定性作用，但是硬件的性能检测和评价比较困难。我们主要介绍综合性测试、评价 硬件性能 的方法。

计算机性能的定义。考量一个计算机性能的基本指标有两个，分别为吞吐率（throughput）和响应时间（response time）。其中，吞吐率表示计算机系统单位时间内完成的工作量；响应时间表示计算机系统完成一个作业从提交开始到作业完成所用的时间。

▶

个人理解 + 适合场景

个人理解：我们以备份文件为例。对于一个大文件，我们希望计算机系统的吞吐率性能足够好，这样处理单文件的能力就会很高。对于很多的小文件，吞吐率高没有什么决定性作用，起决定性作用的是响应时间，我们希望响应时间尽可能的短，这样处理大规模小文件集合的时候就会有优势。那么相应的适用场景也就合理了。

适用场景：对于多媒体应用场景，就相当于大型文件，此时自然希望吞吐率尽可能的高。对于银行、证券交易业务，就相当于大规模小文件集合，我们希望系统的响应时间尽可能的短，这样就可以在单位时间解决更多的小型业务。当然，两者性能均优异自然是最佳选择，对于一些用户体验很重要的应用，比如 ATM、文件服务、Web 服务等等，就需要两者性能均优。

1.4.2 计算机性能的测试

如果不考虑应用背景而直接比较计算机性能，往往通过 程序的执行时间 来衡量。下附程序的执行时间组成图：

▶

程序的执行时间组成图

我们关注的是 用户 CPU 时间。那么如何计算呢？我们引入三个相关计算量：

时钟周期：即一个时钟脉冲信号持续的时间。由于计算机执行一条指令得过程会被分解为不同的小模块进行，因此我们需要控制每一个小模块的执行过程。引入脉冲信号来控制信号的发出和作用的时间等等。
时钟频率：单位时间内的时钟周期数。即上述时钟周期的倒数。
CPI（Cycles Per Instruction）
- 对于一条指令而言：CPI 指的是 一条指令 所需的时钟周期数
- 对于一个程序或一台机器而言：CPI 指的是该程序或机器的指令集中 所有指令平均执行 所需的时钟周期数

计算 用户 CPU 时间 的公式：

\begin{equation*} \begin{aligned} \text{用户 CPU 时间} &= \text{程序总时钟周期数} \times \text{时钟周期} \\ &= \text{程序总时钟周期数} \div \text{时钟频率} \end{aligned} \end{equation*}

补充说明：

显然，用户 CPU 时间与计算机性能成反比
上述三个相关计算量是相互制约的，不存在只提升或下降某一个指标

1.4.5 Amdahl 定律

对于系统中某个部分（软件或硬件）进行更新所带来的系统的性能提升，是取决于这部分原本的运行时间占总运行时间，以及这部分升级了多少倍两者共同决定的，用公式表示 改进后系统的执行时间：

\text{改进后的执行时间} = \frac{\text{改进部分原本占用的时间}}{\text{改进的倍数}}+\text{剩余部分占用的时间}

当然 整体改进倍数 也就可以表示为：

\text{整体改进倍数} = \frac{1}{ \frac{\text{改进部分原本占用的时间}\textbf{比例}}{\text{改进的倍数}} + \text{剩余部分占用的时间}\textbf{比例} }

1.5 本书的主要内容与组织结构

第一章主要介绍：计算机的基本工作原理、计算机系统的基本组成、程序的开发与执行过程、计算机系统的层次结构以及性能评价的基本概念。

第二章主要介绍：各类数据在计算机中的表示与运算。

第三章主要介绍：高级语言中的过程调用和控制语句所对应的汇编指令序列，以及各类数据结构元素的访问所对应的汇编指令。

第四章主页介绍：如何将多个模块链接起来生成一个可执行的目标文件。

2 数据的机器级表示与处理

本章主要从四个方面展开，分别为：数值数据的表示、非数值数据的表示、数据的存储、数据的运算。

2.1 数制和编码

2.1.1 信息的二进制编码

计算机内部所有的信息都采用二进制 01 进行编码
需要编码的机器级数据分为以下两类：
1. 数值数据：整数（带符号、无符号）、浮点数
2. 非数值数据：逻辑数、西文字符、汉字字符
理解真值和机器数的概念

2.1.2 进位计数制

进制表示

二进制：后缀为 B（即 Binary，如 0110B）
八进制：后缀为 O（即 Octal，如 12673O）
十进制：后缀为 D（即 Decimal，如 291D；可省略，即 291）
十六进制：后缀为 H（即 Hexadecimal，如 3F9H；可以前缀 0x 标记，即 0x3F9）

进制转换：一般先将数据转换为二进制，再进行相应转换

R 进制转换为十进制
十进制转换为 R 进制
二、八、十六进制的相互转换

2.1.3 定点与浮点的表示

定点数：小数点位置约定在固定位置的数

定点小数：小数点总是固定在数的最左端，可以用来表示浮点数的尾数部分
定点整数：小数点总是固定在数的最右端，可以用来表示整数

浮点数：小数点位置约定为可浮动的数。对于任意一个实数 X 都可以表示成下面的形式：

X = (-1)^{S} \times M \times R^E

$S$ 取 $0$ 或 $1$ 决定当前实数的正负
$M$ 是一个二进制定点小数，称为实数的尾数。有效位数越多，说明精度越高
$E$ 是一个二进制定点整数，称为实数的阶数。决定小数点的位置
$R$ 称为实数的基数。由数制决定

取值范围：假定浮点数的尾数为纯小数即尾数不为零，则浮点数 $X$ 的绝对值的最小值表示为 $0.00...1 \times R^{-11...1}$ ，最大值表示为 $0.11...1 \times R^{11...1}$ 。假设阶的位数为 $m$ ，尾数的位数为 $n$ 。则浮点数 $X$ 的绝对值真值的取值范围为：

R^{-n} \times R^{-(R^m-1)} \le |X| \le (1-R^{-n}) \times R^{R^m-1}

2.1.4 定点数的编码表示

原码表示法
补码表示法
- 模运算： $\text{对一个负数取模} = \text{模} - |\text{负数}|$
- 补码的定义： $[X]_{\text{补}}=2^n+X$ ，对于 $n$ 位的运算系统，可以表示补码的数据范围为 $-2^{n-1} \le X < 2^{n-1}$
反码表示法
移码表示法

2.2 整数的表示

2.2.1 无符号整数和带符号整数的表示

无符号整数：所有的二进制位都用来表示数值。比如对于 $n$ 位的二进制数，无符号整数的数值范围为 $[0,2^{n} - 1]$

有符号整数：第一位二进制位必须用来进行正负性表示，后 $n-1$ 位用来表示数值。同样对于 $n$ 位的二进制数，有符号整数的数值范围为 $[-2^{n-1}, 2^{n-1})$

2.2.2 C 语言中的整数及其相互转换

C 语言标准中规定：若运算中同时有无符号和带符号整数，则按无符号整数运算

搞懂这张真值比较表即可：

真值比较表

2.3 浮点数的表示

2.3.1 浮点数的表示范围

我们以 32 位浮点数为例。32 位中：

第 0 位为符号位 $\text{(Sign)}$ 。1 表示负数，0 表示正数
第 1 - 8 位为阶数位 $\text{(Exponent)}$ 。采用移码表示，通常需要加上偏执常数 128
第 9 - 31 位为尾数位 $\text{(Fraction)}$ 。规格化尾数的表示形式为 $0.1\text{bb...b}$

正数的最大值： $0.11...1 \times 2^{11...1}=(1-2^{-24}) \times 2^{127}$

正数的最小值： $0.10...0 \times 2^{00...0} = 2^{-1} \times 2^{-128}=2^{-129}$

浮点数的表示范围

2.3.2 浮点数的规格化

分为左规和右规，目的是尽可能多的得到有效位，同时使得浮点数的表示具有唯一性

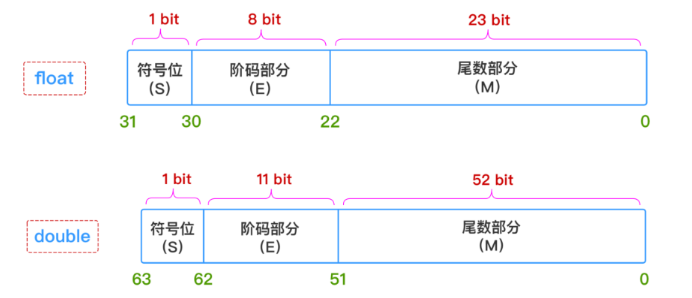
2.3.3 IEEE 754 浮点数标准

与前面提到的规则略有不同。对于下列两种精度的浮点数：有以下规定：

对于尾数：隐藏位 1 还是存在，不过现在不是在小数点右边，而是在小数点左边
对于阶数：同样采用移码的形式，只不过现在的偏执常数不是 $2^{n-1}$ ，而是 $2^{n-1}-1$ 。因此单精度和双精度浮点数的偏执常数分别为 $2^{8-1}-1=127,2^{11-1}-1=1023$

IEEE 754 浮点数标准

对于本目，需要掌握 IEEE 754 规格化小数 与真值之间的转换，转换规则如下：

▶

转换规则

浮点数的 5 种表示形式：

单精度浮点数的各种极端情况：

2.3.4 C 语言中的浮点数类型

主要掌握强制类型转换。

int 到 float 可能丢失有效数字。因为 int 的有效数位比 float 多
int、float 到 double 数值不变
double、float 到 int 可能丢失有效数字或溢出
double 到 float 可能丢失有效数字或溢出

2.4 十进制数的表示

2.4.1 用 ASCII 码字符表示

pass

2.4.2 用 BCD 码表示

pass

2.5 非数值数据的编码表示

2.5.1 逻辑值

1 个二进制数表示 1 个逻辑值。

2.5.2 西文字符

西文字符集的编码是 ACSII 码，一般是 7 位二进制位 $b_6b_5b_4b_3b_2b_1b_0$ 来表示。可能会有第八位 $b_7$ ，该位往往用来进行奇偶校验。

2.5.3 汉字字符

汉字数量庞大，且是表意形的字符，为了在计算机中表示汉字，我们需要处理三个问题，分别是输入表示、机器表示、输出表示：

汉字的输入码：用于对输入的中文字符进行编码
字符集与汉字内码：用于系统内部的存储、查找、传送等处理
汉字的字模点阵码和轮廓描述：用于显示和打印

概念定义：

图像的基本单位是像素，是真实世界的数字表示
图形的往往是数学或程序算法生成的，是虚构的

2.6 数据的宽度和存储

2.6.1 数据的宽度和单位

计算机中数据的 表示宽度 及其单位

二进制信息的最小单位：比特（bit）
最小寻址单位：字节（Byte），其中 1Byte = 8 bit
更大的单位表示：字（word），其中 1 word = 2 bit | 4 bit | 8 bit | 16 bit

计算机中数据的运算、存储、传输的 部件宽度 及其单位

数据通路宽度：字长

2.6.2 数据的存储和排列顺序

对于一个 32 bit 的数 1000 0000 0000 0000 0000 0000 0000 0110 而言，我们定义：

最高有效位（MSB，Most Significant Bit）：上述 32 位数的最左边的一位 1
最低有效位（LSB，Least Significant Bit）：上述 32 位数的最右边的一位 0
最高有效字节（MSB，Most Significant Byte）：上述 32 位数的最左边的一字节 1000 0000
最低有效字节（LSB，Least Significant Byte）：上述 32 位数的最右边的一字节 0000 0110

现代计算机都是对字节进行编址方式。由于程序中对每个数据只给定一个地址，那么对于多字节的数据如何根据仅有的一个地址进行 CPU 的内存分配呢？这就是经典的字节排序问题。现在介绍两种内存分配方式：大端方式、小端方式

大端方式：最低有效字节存放在最高位。对应的机器码中最低有效字节在最右端，例如数值 0x0000001E 在大端方式下存储为 00 00 00 1E
小端方式：最低有效字节存放在最低位。对应的机器码中最低有效字节在最左端，例如数值 0x0000001E 在小端方式下存储为 1E 00 00 00
举例说明：对于机器数 0xFFFFFFF6 而言，下面的表示方式中，左侧为小端存储，右侧为大端存储

2.7 数据的基本运算

学完了基本的数据表示以后，让我们开始学习数据的基本运算。高级语言中涉及到的各种运算，都会被编译成底层的算术运算指令和逻辑运算指令实现，本目要介绍的也就是其中的运算逻辑。

2.7.1 按位运算和逻辑运算

按位运算

\|	&	~	^
按位或	按位与	按位取反	按位异或

逻辑运算

\|\|	&&	!
逻辑或	逻辑与	逻辑非

2.7.2 左移运算和右移运算

无符号整数采用 逻辑移位：

左移：高位移出，低位补 0。如果移出为 1，则溢出
右移：高位 补 0，低位移出

有符号整数采用 算数移位：

左移：高位移出，低位补 0。如果左移前后符号位不同，则溢出
右移：高位 补符号，低位移出

2.7.3 位扩展运算和位截断运算

扩展操作：在短数向长数转换时

有符号整数采用 符号扩展：前方补符号位
无符号整数采用 0 扩展：前方补 0

▶

code

#include <stdio.h>

int main() {
    short int si = -32768;
    unsigned short usi = si;
    int i = si;
    unsigned ui = usi;
    
    printf("si  = \t%hd\t%x\n", si, si);
    printf("usi = \t%hu\t%x\n", usi, usi);
    printf("i   = \t%d\t%x\n", i, i);
    printf("ui  = \t%u\t%x\n", ui, ui);
}

上述代码在 32 位大端机器上的输出：

si  =   -32768  8000
usi =   32768   8000
i   =   -32768  ffff8000
ui  =   32768   8000

分析：

si 和 usi 是同一个机器数的不同真值结果，由于数位没有长短的变化，故十六进制表示结果相同
i 是有符号整数的位扩展，采用符号扩展，补充符号位 1，故向前补充了 16 个 1
ui 是无符号数的位扩展，采用 0 扩展，补充 0，故向前补充了 16 个 0

截断操作：在长数向短数转换时

有符号整数，高位直接丢弃
无符号整数，高位直接丢弃

▶

code

#include <stdio.h>

int main() {
    int i = 32768;
    short si = (short)i;
    int j = si;

    printf("i  = \t%d\t%x\n", i, i);
    printf("si = \t%hd\t%x\n", si, si);
    printf("j  = \t%d\t%x\n", j, j);
}

上述代码在 32 位大端机器上的输出：

1
2
3

i  =    32768   00008000
si =    -32768  8000
j  =    -32768  ffff8000

分析：

i 的真值和机器数很显然
si 的机器数就是将 i 的机器数截取了后 16 位的结果，在识别为有符号数以后，得到的真值就是最小的负数 -32768
j 是有符号整数的位扩展运算，补充符号位 1
可以发现了 截断错误，而这种错误编译器一般是不会发现的！

2.7.4 整数加减运算

整数加/减运算部件

部件解读：对于无符号整数和有符号整数而言，都可采用该运算部件进行运算

输入：
1. 运算数 A：整数 A 的补码 01 序列
2. 运算数 B：整数 B 的补码 01 序列
3. 判别数 Sub：A+B 时 Sub=0，A-B 时 Sub=1
输出：
1. 结果 Sum：表示整数 A+B 的计算结果
2. 零标志 ZF：表示 A+B 是否为 0
3. 符号标志 SF：表示计算结果 Sum 的有效范围内的最高位二进制数值
4. 溢出标志 OF：判断 有符号整数 的相加结果是否溢出。计算方式：
  - 若 A 与 B’ 首位同号且与 Sum 的首位不相同，则计算溢出，OF = 1
  - 反之则计算未溢出，OF = 0
5. 进/借位标志 CF：判断 无符号整数 的相加结果是否溢出。计算方式：
  - 对于加法：此时的判别数 Sub = 0
    - 若有进位，即 Cout = 1，则对于当前加法器表示计算溢出，CF = 1
    - 若没有进位，即 Cout = 0，则没有计算溢出，CF = 0
  - 对于减法：此时的判别数 Sub = 1
    - 若有借位，则 Cout = 0，则对于当前加法器表示计算结果是负数，即计算溢出，CF = 1
    - 若没有借位，则 Cout = 1，则对于当前加法器表示计算结果是正数，即计算未溢出，CF = 0
  - 综上所述：
    $\text{CF} = \text{Sub} \oplus \text{Cout}$

▶

举例说明

对于两个机器数 x = 1000 0110 和 y = 1111 0110

加法：计算 x + y

\begin{aligned}&\text{MUX}:\begin{cases}y' &= y \\\text{Sub} &= 0\end{cases}\\&\text{Adder}:\begin{cases}x: & 1000\ 0110 \\y'= y: & 1111\ 0110 \\\text{Sub}: & 0\end{cases}\\&\text{Result}: 1 \ 0111\ 1100\\&\text{Signals}:\begin{cases}\text{ZF} = 0 \\\text{SF} = 0 \\\text{OF} = 1 \\\text{CF} = 1\end{cases}\\&\text{Real Value}:\begin{cases}\text{signed}: &124(134+246-2^8)\\\text{unsigned}: &124(134+246-2^8)\end{cases}\end{aligned}

减法：计算 x - y

\begin{aligned}&\text{MUX}:\begin{cases}y' &= \overline{y} \\\text{Sub} &= 1\end{cases}\\&\text{Adder}:\begin{cases}x: & 1000\ 0110 \\y'=\overline{y}: & 0000\ 1001 \\\text{Sub}: & 1\end{cases}\\&\text{Result}: 0 \ 1001\ 0000\\&\text{Signals}:\begin{cases}\text{ZF} = 0 \\\text{SF} = 0 \\\text{OF} = 0 \\\text{CF} = 1\end{cases}\\&\text{Real Value}:\begin{cases}\text{signed}: &-112 \\\text{unsigned}: &144(134-246+2^8)\end{cases}\end{aligned}

对于 n = 8 的情况而言，数据范围是：

\begin{cases}\text{signed}: &[-2^{n-1},2^{n-1}) &=& [-128,127] \\\text{unsigned}: &[0,2^n) &=& [0,255]\end{cases}

2.7.5 整数乘除运算

整数乘法中。两个 n 位的整数相乘得到一个 2n 位整数，但是一般只保留低 n 位，高 n 位舍弃。判断乘法溢出 规则如下：

对于无符号整数乘法：若高 n 位全 0 则没溢出，反之溢出
对于有符号整数乘法：若高 n 位全等于低 n 位的首尾，则没溢出，反之溢出

整数除法中。两个 n 位整数相除，溢出异常和小数舍去 规则如下：

除了最小负数除以 -1 会发生溢出，以及除 0 会发生异常以外，其余情况全部是正常运算
无论是带符号还是无符号，所有产生的小数部分全部舍弃，效果就是向 0 取整

2.7.6 常量的乘除运算

常量乘法运算中。由于直接当做整数进行乘法会导致更高的消耗，因此编译器一般会将其拆分为移位运算与加减运算的综合运算

比如表达式 x * 20 中的 20 会被二进制拼凑分解为 2^4 + 2^2，也就是将 x 左移 4 位的结果与 x 左移 2 位的结果相加

常量除法运算中。同样由于时间开销极大，也是采用移位进行优化，但是与加法略有不同，对于除数是一个 $2^k$ 整数的形式时：

若被除数是 无符号数 或者 有符号正数，直接低位丢弃，高位按照相应的规则补齐
若被除数是 有符号负数，且移出低位时有 1，则需要先将被除数加上 $2^k-1$ ，再执行第一步的操作

2.7.7 浮点数运算

以浮点数加减为例。

转换：转换为二进制数
对阶：小阶往大阶靠拢
尾数加减
尾数规格化：只能让 1 出现在小数点的左边一位
阶码溢出判断

3 程序的转换及机器级表示

上一章节我们学习了 数据的机器级表示，本章我们将学习 程序的机器级表示。包括我们写的屎山是怎么转化成机器能理解的 01 序列的（程序的转换）以及机器理解东西的规则是什么（机器级表示，以 IA-32 指令集为例）。

程序的转换 大约用下面这个流程图就能概括了：

\begin{aligned}\text{源代码 $\xrightarrow[]{\text{预处理}}$ 源代码 $\xrightarrow{\text{编译}}$ 汇编代码 $\xrightleftharpoons[\text{反汇编}]{\text{汇编}}$ 机器代码 $\xrightarrow[]{\text{链接}}$ 机器代码}\end{aligned}

机器级表示 无法直接阅读，只能从更高层面的汇编来理解。从上图可以看出，汇编代码可以从「源代码编译」而来，也可以从「机器代码反汇编」而来。本章主要就是按 $\text{AT\&T}$ 格式对上述两种来源的汇编代码进行分析和理解。

本章内容梗概：

3.1 节：概述高级语言到汇编语言到机器语言的转换；
3.2 节：概述 IA-32 指令集的三个主要方面，分别为 数据类型及其存储格式、寄存器存取数据的逻辑、机器指令的汇编格式，为后续小节的详细展开做铺垫；
3.3 节：详细展开 机器指令的汇编格式；
3.4、3.5 节：以 C 语言为高级语言示例，详细展开 数据类型及其存储格式、机器指令的汇编格式；
3.6 节：分析异常情况的汇编表示和内部逻辑。

其实很多时候并非写代码才会让电脑起反应，然后根据翻译得到的机器指令做事，我们随便碰些什么都对应很多的指令。下图是我对 读、写、存文件 的可视化展示，以此来加强对计算机内部运作机理的宏观理解：

wdf-is-sys

补充其中的几个概念：

硬盘 (SSD/HDD)：持久存储设备
内存 (RAM)：临时存储设备
中央处理器 (CPU)：中央处理单元

下面经常出现的 寄存器 (Register) 就存在于 CPU 中，作为存储数据的媒介而存在，存取效率极高，也因此决定了 CPU 的处理效率和整体系统的性能。

本章我们要学的「指令集」其实是 CPU 运作机理的一个重要部分。它定义了 CPU 理解和执行指令的规则和方法，也是程序员和编译器与 CPU 交互的接口。

3.1 程序转换概述

3.1.1 机器指令及汇编指令

计算机只认识机器指令，但是机器指令只是一个 01 位串，可读性很差，因此引入汇编指令用于助记。由机器指令组成的程序叫机器语言程序，由汇编指令组成的程序叫汇编语言程序。机器语言程序和汇编语言程序都是机器级程序。将汇编语言转化为机器语言的程序叫 汇编程序，将机器语言转化为汇编语言的程序叫 反汇编程序。

但是汇编语言程序还是很抽象，因此引入高级语言程序。现在我们要解决的是如何将高级语言程序转化为机器语言程序。至于如何转化能够使得时间、空间都最优，这是编译优化要解决的事，本课程不予讨论。

3.1.2 指令集体系结构

回看 1.3 节可以发现，指令集体系结构 $\text{(Instruction Set Architecture，简称 ISA)}$ 是连接计算机硬件和软件之间的桥梁，将物理上的计算机硬件抽象成了逻辑上的虚拟计算机，称为机器语言级虚拟机。

ISA 定义了机器语言级虚拟机的所有功能，是一套 与 CPU 交互 的规则。

3.1.3 生成机器代码的过程

本目介绍高级语言转化为机器语言的过程，以 C 语言该高级语言为例。假设当前有一个 C 语言文件 main.c，利用 gcc 工具可以实现。

预处理：在源程序中插入所有用 #include 命令指定的文件和用 #define 声明指定的宏。生成的 main.i 是 文本文件
1
gcc -E main.c -o main.i
编译：将预处理后的源程序编译成汇编语言程序。生成的 main.s 是 文本文件
1
gcc -S main.i -o main.s
汇编：通过汇编程序将编译出来的汇编语言程序转化为可重定位的机器语言程序。生成的 main.o 是 二进制文件
1
gcc -c main.s -o main.o
链接：将多个可重定位的机器语言程序以及库程序链接为可执行文件
1
gcc main.o -o main

上述第三步汇编出来的二进制文件 main.o 是不可读的，但是我们可以通过将其反汇编成文本文件，进而可读。可以采用 objdump 工具，通过 -d 参数命令将其反汇编为由汇编语言构成的文本文件，命令如下：

1	`objdump -d main`

需要补充的一点是：本书中的汇编语言程序的格式采用 $\text{AT\&T}$ ，这也是 gcc 和 objdump 使用的默认汇编格式。

3.2 IA-32 指令系统概述

3.2.1 数据类型及其格式

IA-32 支持的数据类型及格式与 C 语言之间的对应关系：

C 语言声明	Intel 操作数类型	汇编指令长度后缀	存储长度(位)
`(unsigned) char`	整数/字节	$b$	`8`
`(unsigned) short`	整数/字	$w$	`16`
`(unsigned) int`	整数/双字	$l$	`32`
`(unsigned) long int`	整数/双字	$l$	`32`
`(unsigned) long long int`	-	-	`2*32`
`char *`	整数/双字	$l$	`32`
`float`	单精度浮点数	$s$	`32`
`double`	双精度浮点数	$l$	`64`
`long double`	扩展精度浮点数	$t$	`80/96`

3.2.2 寄存器组织和寻址方式

寄存器组织：共有三大类

寄存器组织

8 个通用寄存器，其中
- EAX, EBX, ECX, EDX 均为 32 位寄存器
- AX, BX, CX, DX 均为 16 位寄存器
- AH, BH, CH, DH 均为高 8 位寄存器
- AL, BL, CL, DL 均为低 8 位寄存器
2 个专用寄存器
6 个段寄存器

寻址方式：

立即寻址：指令直接给出操作数。准确的说不用寻址了；
寄存器寻址：指定寄存器 R 的内容为操作数。在寄存器中找数据；
存储器寻址：基址+变址 × 比例因子+偏移地址。在内存或者硬盘中找数据。

存储器寻址示例 - AT&T 格式汇编

3.2.3 机器指令格式

正如上面所言，机器指令本质上就是一个人为定义的含有某些意义的 01 序列，查询相应的表可以得知对应的汇编语言格式。不需要记忆多少东西，遇到不懂的直接查表即可。

举个例子。下方表格展示了一个经典的转换，怎么转换不重要，重要的是能理解对应汇编语言的逻辑：

机器语言（16 进制格式）	汇编语言（AT&T 格式）
`C744 2404 0100 0000`	`movl $0x1, 0x4 (%esp)`

3.3 IA-32 常用指令类型及其操作

3.3.1 传送指令

符号辨析： $\text{R}$ 即 $\text{Register}$ 表示取寄存器操作数， $\text{M}$ 即 $\text{Memory}$ 表示取存储器操作数， $\text{mov}$ 即 $\text{Move}$ 用于数据传送， $\text{lea}$ 即 $\text{Load Effective Address}$ 用于地址计算。

数据传送语句：mov 0x8(%ebp,%edx,4), %eax 实现的功能为 R[eax] = M[R[ebp] + R[edx] * 4 + 8]。表示将计算出来的地址 R[ebp] + R[edx] * 4 + 8 对应的在存储器中的值 M[R[ebp] + R[edx] * 4 + 8] 赋给寄存器 %eax，此时寄存器中存储的信息为操作数的值 R[eax]。

地址计算语句：lea 0x8(%ebp,%edx,4), %eax 实现的功能为 R[eax] = R[ebp] + R[edx] * 4 + 8。表示将计算出来的地址 R[ebp] + R[edx] * 4 + 8 赋给寄存器 %eax，此时寄存器中存储的信息为操作数的地址 R[eax]。

3.3.2 定点算数运算指令

加减乘除分别为：add, sub, mul, div，都是将「源地址」的值运算到「目的地址」，即左边对应的值运算到右边对应的值。可以记忆为右边的数 +=, -=, *=, /=。

3.3.3 按位运算指令

常用的有按位运算，以及算数、逻辑的左移和右移。按位运算中有一个用于判定单个数情况的指令为 test，test 不修改右边对应的值，其余都遵循上述「左的值运算到右进而改变右」的规则。

移位指令大约有：shl, sal, shr, sar，分别为逻辑左移、算数左移、逻辑右移、算数右移。

3.3.4 控制转移指令

常用的有无条件转移，对应 C 语言中的 goto 关键字，汇编表示为 jmp 等。以及有条件转移，比如 je, jne 等，取决于逻辑运算的结果。转移的位置统称为「目标地址」。

3.4 C 语言程序的机器级表示

用任何汇编语言或高级语言编写的 源程序 都必须翻译（汇编、解释或编译）成以指令形式表示的 机器语言，才能在计算机上运行。本节高级语言选用 C 语言，机器语言选用 IA-32 指令系统，简单介绍高级语言转化为机器语言的过程。

3.4.1 过程调用的机器级表示

CALL 调用指令：在执行调用过程之前需要将返回地址压入栈

RET 返回指令：在返回调用过程之前从栈中取出返回地址

过程调用的执行步骤（记调用者为 P，被调用者为 Q）

步骤	过程
P 将参数存储到 Q 可以访问到的地方	按参数列表从右往左依次压入栈
P 保存返回地址（即调用函数的下一个语句）并将控制权给 P	将返回地址入栈并执行 CALL 指令
Q 保存 P 的现场并为自己的非静态变量分配空间	一般由调用与被调用过程共同保存通用寄存器中的现场
执行 Q 的函数体	—
Q 恢复 P 的现场并释放局部变量空间	恢复现场并释放局部变量空间
Q 取出返回地址并将控制权给 P	通过 RET 指令

3.4.2 选择语句的机器级表示

主要由常用指令组合而成，相比于过程调用更加简单。

3.4.3 循环语句的机器级表示

同选择语句。

3.5 复杂数据类型的分配和访问

3.5.1 数组的分配与访问

采用相对寻址，大一学习 C 语言的数组时就学过相关概念了，关键有两点：

知道数组存的是什么类型的数据（进而知道每一个元素占用多少字节）
知道数组首地址。以二维数组为例，运算公式就是 &a + (typeof a) * (i * M) + j，其中 typeof a 就表示单个元素的字节数，i, j 就表示下标索引，M 就表示行数（默认按行优先规则）

3.5.2 结构体数据的分配与访问

采用首地址+偏移的逻辑分配与访问数据，与数组类似。同时，一个结构体存储所有字段的数据。

3.5.3 联合体数据的分配与访问

同样采用首地址+偏移的方式分配和访问数据。一个联合体在同一时刻只存储一种数据类型。即相同的位序列可以在不同时刻存储不同的数据类型变量。

3.5.4 数据的对齐

对于 32 位 OS 而言，存储器一行存储 32 位共 4 个字节，计算机系统一次访问存储空间只能读写固定长度的位。假定最多可以读写 64 位，则称为 8 字节宽的存储器机制。一般采用 按边界对齐 的对齐策略，尽管这样会浪费一些存储空间，但是有利于数据的快速访问。

▶

举两个例子

一、对齐实例。对于 5 个变量 int a; short b; double c; char d; short e;

按边界对齐：

边界不对齐

二、结构体实例。全部按 4 字节对齐，末尾可能有插空

struct A {
    int    i;
    short si;
    char   c;
    double d;
};

struct B {
    int    i;
    short si;
    double d;
    char   c;
};

3.6 越界访问和缓冲区溢出

越界访问和缓冲区溢出其实是一个东西，只不过缓冲区溢出是单独针对栈空间中对局部数组进行了越界访问。一般而言的越界访问往往表示错误访问了栈空间中的返回地址导致程序出现意想不到的错误。

4 程序的链接

在编写大型程序时，为了 提升效率 以及 不断复用，往往需要模块化开发，这就需要我们对多个分散的源代码片段进行整合。目前的整合方法是：首先对每一个源代码片段 $\text{(*.c)}$ 分开进行编译、汇编生成对应的可重定位目标文件 $\text{(*.o 或 *.obj)}$ ，然后通过链接器 $\text{(linker)}$ 将所有的可重定位目标文件与使用到的其他库的可重定位目标文件整合形成最终的可执行文件 $\text{(*.exe)}$ 。其中库文件包含静态库 archive 文件 $\text{(*.a)}$ 和动态共享库 shared object 文件 $(\text{*.so})$ 。

本章首先通过简单介绍源代码向可执行文件转换的过程，引出符号解析和重定位的粗略含义。然后详细介绍 UNIX 系统中可重定位目标文件和可执行文件的 ELF 格式。最后详细介绍可重定位目标文件中关于符号定义和符号引用到底是如何解析的，以及链接生成可执行文件的过程中，这些符号又是如何重定位到可执行文件中的。

4.1 编译、汇编和静态链接

模块化的好处：

便于维护与共享。一个地方出问题了修改后重新编译即可，共享也很好理解。
时间效率高。原因同上，不需要全部修改，单点修改即可解决。

4.2 目标文件格式

4.2.1 ELF 目标文件格式

Executable and Linkable Format，简称 ELF。是 UNIX 系统下对可重定位目标文件 $\text{(*.o)}$ 、可执行目标文件 $\text{(*.exe)}$ 和共享库文件 $\text{*.so}$ 的规范化格式，本目只介绍前两者的格式信息。

4.2.2 可重定位目标文件格式

即 $\text{(*.o 或 *.obj)}$ 文件。

4.2.3 可执行目标文件格式

即 $\text{(*.exe)}$ 文件。

4.3 符号解析

4.3.1 符号和符号表

每一个可重定位文件 demo.o 都有一个符号表用来记录本模块的符号信息

4.3.2 符号解析

符号解析的目的：将本模块中引用的符号与某个目标模块中的定义符号建立关联

建立关联的原理：每个定义符号在代码段或数据段中都被分配了存储空间，将引用符号与定义符号建立关联后，就可在重定位时将引用符号的地址重定位为相关联的定义符号的地址

链接器符号：

Global symbols（模块内部定义的全局符号）
External symbols（外部定义的全局符号）
Local symbols（本模块的局部符号）

（1）全局符号的强、弱特性：

强符号：函数的定义、已初始化的全局变量
弱符号：函数的声明、未初始化的全局变量

符号解析定义的规则：由于每个符号仅占一处存储空间，因此有以下规则

强符号不能多次定义
若一个符号被定义为一次强符号和多次弱符号，则按强定义为准
若有多个弱符号定义，则任选其中一个

（2）符号解析过程：

4.3.3 与静态库的链接

按照符号引用顺序进行静态链接。引用在前，定义在后。

4.4 重定位

只关心全局变量和静态模块变量，对于所有的局部变量全部忽略。

4.4.1 重定位信息

4.4.2 重定位过程

（一）相对重定位方式 R_386_PC32

根据相对位置进行简单的加减运算得出相对的虚拟地址信息。

（二）绝对重定位方式 R_386_32

直接给出引用信息的虚拟内存地址。

至此本课程介绍的内容已全部结束，但其实还有动态链接值得玩味，我大致梳理一下脉络。所谓的静态库解决了代码复用的问题，但也有不足之处，假如磁盘中成千上万个可执行文件都引用了静态库中的某个文件，那么显然就会造成大量存储空间的浪费。同时，假如这些可执行文件同时运行，那么内存中又会读入上述被引用文件的大量重复副本。无论是存储空间还是内存，都是极大的浪费，而动态共享库很好的解决了这个问题，用到哪个库文件直接动态调用不就好了！除此之外，假如我需要维护升级某个静态库文件，那么那些引用该静态库文件的程序都需要重新链接进行更新，这显然是及其不方便且容易出错的。

GPA > 4th-term

SysBasic

https://blog.dwj601.cn/GPA/4th-term/SysBasic/

作者

Mr_Dwj

发布于

2024年3月21日

更新于

2024年11月14日

许可协议

PyAlgo 上一篇

DataStructureClassDesign 下一篇

SysBasic

计算机系统基础

前言

1 计算机系统概述

1.4.2 计算机性能的测试

1.4.5 Amdahl 定律

1.5 本书的主要内容与组织结构

2 数据的机器级表示与处理

2.1 数制和编码

2.1.1 信息的二进制编码

2.1.2 进位计数制

2.1.3 定点与浮点的表示

2.1.4 定点数的编码表示

2.2 整数的表示

2.2.1 无符号整数和带符号整数的表示

2.2.2 C 语言中的整数及其相互转换

2.3 浮点数的表示

2.3.1 浮点数的表示范围

2.3.2 浮点数的规格化

2.3.3 IEEE 754 浮点数标准

2.3.4 C 语言中的浮点数类型

2.4 十进制数的表示

2.4.1 用 ASCII 码字符表示

2.4.2 用 BCD 码表示

2.5 非数值数据的编码表示

2.5.1 逻辑值

2.5.2 西文字符

2.5.3 汉字字符

2.6 数据的宽度和存储

2.6.1 数据的宽度和单位

2.6.2 数据的存储和排列顺序

2.7 数据的基本运算

2.7.1 按位运算和逻辑运算

2.7.2 左移运算和右移运算

2.7.3 位扩展运算和位截断运算

2.7.4 整数加减运算

2.7.5 整数乘除运算

2.7.6 常量的乘除运算

2.7.7 浮点数运算

3 程序的转换及机器级表示

3.1 程序转换概述

3.1.1 机器指令及汇编指令

3.1.2 指令集体系结构

3.1.3 生成机器代码的过程

3.2 IA-32 指令系统概述

3.2.1 数据类型及其格式

3.2.2 寄存器组织和寻址方式

3.2.3 机器指令格式

3.3 IA-32 常用指令类型及其操作

3.3.1 传送指令

3.3.2 定点算数运算指令

3.3.3 按位运算指令

3.3.4 控制转移指令

3.4 C 语言程序的机器级表示​

3.4.1 过程调用的机器级表示​

3.4.2 选择语句的机器级表示

3.4.3 循环语句的机器级表示

3.5 复杂数据类型的分配和访问

3.5.1 数组的分配与访问

3.5.2 结构体数据的分配与访问

3.5.3 联合体数据的分配与访问

3.5.4 数据的对齐

3.6 越界访问和缓冲区溢出

4 程序的链接

4.1 编译、汇编和静态链接

4.2 目标文件格式

4.2.1 ELF 目标文件格式

4.2.2 可重定位目标文件格式

4.2.3 可执行目标文件格式

4.3 符号解析

4.3.1 符号和符号表

4.3.2 符号解析

4.3.3 与静态库的链接

4.4 重定位

4.4.1 重定位信息

4.4.2 重定位过程

3.4 C 语言程序的机器级表示

3.4.1 过程调用的机器级表示