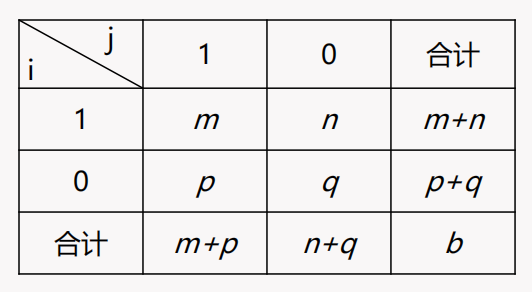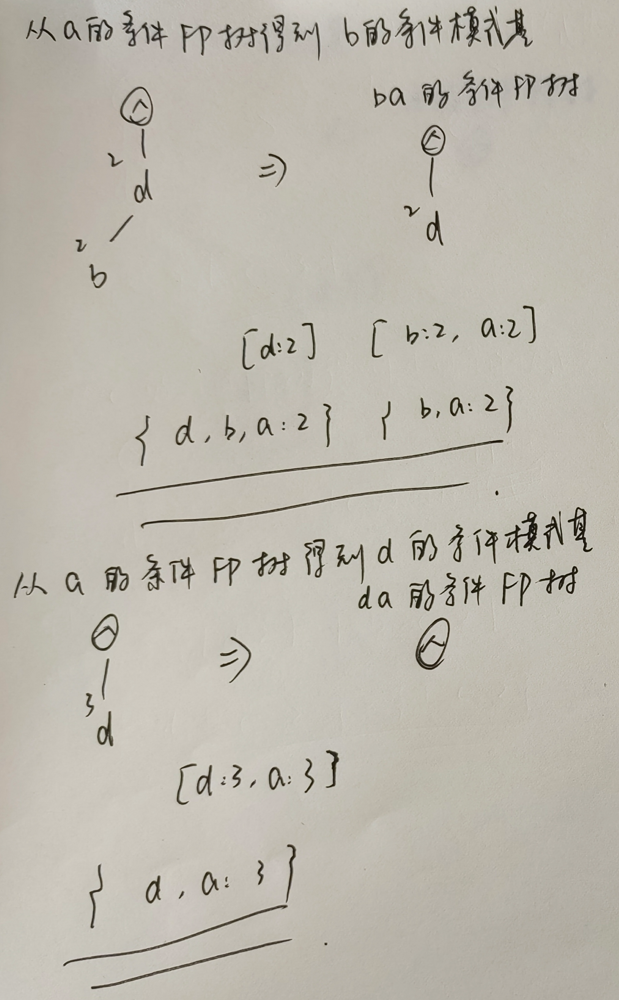数据挖掘
前言¶
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN 号 |
|---|---|---|---|---|---|
| 数据挖掘 | 《数据挖掘:原理与应用》 | 1 | 丁兆云,周鋆,杜振国 | 机械工业出版社 | 978-7-111-69630-8 |
为什么要学这门课?
数据量在进入信息化时代后指数级增长,显然这些数据一定具有某种价值。之前看到过这样的说法 “你能想到和做到的,前人都已经想到和做到了”。虽然这样的说法不具有绝对性,但是个人认为对于大多数人都是适用的。也就是说,人类的行为甚至是万物的变迁都是符合统计学规律的,而这些规律都藏在浩瀚的数据之中。
至于这门课安排在此的意义,个人认为是对大二时机器学习课程的一个补充。
会收获什么?
数据预处理的基本策略,新学关联分析和异常检测算法,重温聚类算法。
1 绪论¶
科学发展范式
实验(经验)科学 \(\to\) 理论科学 \(\to\) 计算科学 \(\to\) 数据科学。
一些定义
数据的定义:分为结构化和非结构化数据。结构化例如关系数据库的含有显式的属性和取值,非结构化例如文本、图像、音频和视频。
知识的定义:有意义的信息或模式,具备典型性、新颖性、时效性、准确性、实用性。
数据挖掘的定义:从数据中提取知识。
数据挖掘的过程:数据预处理、算法实践、解释评估。
属性分类
- 定性。二元属性、标称属性、序数属性;
- 定量。即数值属性。区间数值可以取负数,比率数值取不了负数。
数据的宏观特性
- 中心趋势度量。用来描述数据集中心位置的统计量,它反映了数据的平均水平或典型值。例如:
- 算术平均数(受计算数据的影响大);
- 调和平均数(特定场景);
- 中位数(适用于序数申诉信,表示位置信息,不受极差影响);
- 众数(不受极差影响)。
- 离散度度量。用来描述数据分布的广泛程度,即数据值偏离其中心趋势的程度。例如:
- 极差(适用于数据极端值较少且分布不复杂的场景);
- 标准差(解释性比方差更好,反应数据与均值之间的关系,对极端值敏感);
- 分位数(反应数据内部的离散程度,容易忽略极端数据)。
可视化策略
- 箱型图、五数概括、直方图。有助于可视化 单个属性 的数据分布;
- 饼图。有助于可视化 单个属性 的数据占比;
- 散点图。有助于可视化 两个属性 的相关关系。
邻近性度量
所谓邻近性度量,可以简单的将其理解为计算任意两个数据对象之间的距离,只不过这里的距离一般用相异性来表示(相似性就是 \(1-\text{相异性}\))。由于数据对象的属性有很多种类,不同种类的邻近性度量方法不同,因此当我们在对两个数据对象进行邻近性度量时,需要根据属性的类别分组计算。下面讲一下不同属性类别的邻近性度量方法:
1)标称属性
我们在实际计算两个数据对象标称属性的相似性或相异性时,一般为了便于计算需要对其进行编码,然后再比较两个数据对象的所有标称属性中相同或相异的编码个数占总标称属性的数量。常见的标称属性有:籍贯、学历等等;
2)二元属性
与标称属性类似同样需要进行编码,但会取决于二元属性的对称性。
假设两个数据对象在二元属性上的取值情况如上图所示:都取 \(1\) 的数量为 \(m\),都取 \(0\) 的数量为 \(q\),取 \((1,0)\) 的数量为 \(n\),取 \((0,1)\) 的数量为 \(p\)。则有以下相异性计算公式:
-
对称二元属性。相异性为 \(\displaystyle \frac{p+n}{m+n+p+q}\)。常见的对称二元属性有:朋友、配偶;
-
非对称二元属性。相异性为 \(\displaystyle \frac{p+n}{m+n+p}\),因为两个取值都为1的情况比取值都为0的情况更有意义。常见的非对称二元属性有:上下级、父母与子女、教师与学生;
3)数值属性
对于两个数值型的数据对象 \(\boldsymbol x\) 和 \(\boldsymbol y\),定义了以下两种邻近性度量指标:
-
闵可夫斯基距离。取值范围为 \([0,+\infty]\)。\(h = 1\) 为曼哈顿距离,\(h = 2\) 为欧氏距离,\(h = \infty\) 为切比雪夫距离(上确界距离)。如下式:
\[ \begin{aligned} \text{闵可夫斯基距离:}& d(\boldsymbol x,\boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_h \\ \text{曼哈顿距离:}& d(\boldsymbol x,\boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_1 \\ \text{欧几里得距离:}& d(\boldsymbol x,\boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_2 \\ \text{切比雪夫距离:}& d(\boldsymbol x,\boldsymbol y) = \| \boldsymbol x - \boldsymbol y \|_\infty = \max(\boldsymbol x - \boldsymbol y) \end{aligned} \] -
余弦距离。取值范围为 \([0, 2]\)。就是两个数据对象的余弦值的相反数加 1 (这很巧妙的利用了余弦值进行了相似性度量并且还确保了计算结果的非负性)。这个度量方法偏向于语言上描述两个对象的差异性,并不适合进行度量测量 (metric measure),因为其不具备三角不等式关系。如下式:
\[ d(\boldsymbol x,\boldsymbol y) = 1 - \cos < \boldsymbol x,\boldsymbol y> \]
4)序数属性
使用排名法对属性的每一个可能的取值进行编码,然后归一化到 \([0,1]\) 范围内,最后就可以使用上面的数值属性的方法进行两个数据对象的邻近性度量。
5)混合属性
如果出现了不止一种上述类别的属性,可以采用 加权平均 的方式进行邻近性度量。
2 数据预处理¶
数据决定上限,模型和算法只是尽可能逼近这个上限,因此数据的质量是核心所在。数据的质量可以被描述为这几个方面:准确性、完整性、一致性、合时性、可信度、解释性。
接下来我们主要介绍数据预处理的几个主要任务,将数据处理成模型可接受的形式并且提升数据的质量。
2.1 数据清理¶
大约需要处理两类问题:缺失值处理、噪声处理。
关于缺失值处理。
- 显然我们可以直接删除含有缺失属性的元组;
- 也可以进行缺失值填充。填充策略比较多,简单点可以用平均数、众数等策略进行填充,也可以用前推法、后推法、插值法、滑窗均值法等策略进行填充,还可以用贝叶斯等概率策略进行填充。
关于噪声处理。
-
可以用箱型图去掉噪声;
-
也可以对数据做平滑处理。平滑策略有很多,例如:函数拟合平滑、近邻局部平滑、指数平滑。
-
函数拟合平滑比较显然,就是利用线性回归拟合一个函数即可;
-
近邻局部平滑(分箱法)。我们将原始数据排序后,通过「等深分箱(按元素数量)」或「等宽分箱(按元素值域)」或「自定义分箱」等策略划分为不同的子集,然后对每一个子集进行平滑处理,子集可以用均值、中位数、边界、窗口均值等策略做平滑处理;
-
指数平滑(递推法)。定义权重参数 \(\alpha \in (0,1)\),原始数据记作 \(x_1,x_2,...,x_n\),平滑后数据记作 \(s_1,s_2,...,s_n\),则有:
\[ s_i = \alpha x_i + (1 - \alpha) s_{i-1} \]
-
2.2 数据集成¶
借鉴数据库的逻辑,将多源数据通过外键集成到一个完整的数据集合中。可以理解为横向的升维与纵向的增加数据。
2.3 数据规约¶
所谓数据规约就是降低数据集的规模。大约有三种策略分别为:降维、降数据、数据压缩。其中:
- 降维。可以采用对应的机器学习策略。参考之前的笔记 特征映射;
- 降数据。可以采用简单随机抽样或者分层抽样;
- 数据压缩。就是从编码角度进行数据编码和数据压缩。
2.4 数据规范化¶
数据规范化就是所谓的「归一化」方法,从而避免不同属性的量纲之间的影响。常用的有:
- 最大最小规范化。规范公式为 \(\displaystyle x'= \frac{x - x_{\min}}{x_{\max} - x_{\min}}(r - l) + l\)。缺点是容易受离群点的影响,且测试数据可能会超过阈值 \([l,r]\)。
- 均值标准差规范化。规范公式为 \(\displaystyle x'=\frac{x - \overline{x}}{\sigma_x}\)。缺点是计算量相对更大。
- 零均值规范化。规范公式为 \(\displaystyle x'=\frac{x}{10^j}\),其中 \(j\) 为使得 \(\displaystyle \frac{\max{|x|}}{10^j}<1\) 的最小取值。
2.5 数据离散化¶
数据离散化就是对连续属性值的属性进行离散化操作。从而适用于只能处理离散属性的场景。
3 关联分析¶
人们在购物时,有些东西往往是捆绑购买的,如果我们想要通过客户的购物记录挖掘出捆绑消费的物品并将这些物品摆放在一起,可以显著提升商品的销售量,那么如何挖掘出这样的捆绑关系呢?本章我们学习一种无监督学习方法:关联分析。一般来说购买了某个物品是一个很重要的事情,因此购物记录的属性全都是非对称二元属性。本章最后再补充一下序列的关联分析。
3.1 基本概念¶
基本定义:
-
某一个属性称为 项 Item;
-
一些属性的集合称为 项集 Itemset;
-
关联分析的数据集称为事务集,其中每一行表示一个 事务 transaction;
Warning
事务和项集并不是一回事。事务可以看做一条实际的购物记录,表示某个顾客买了哪些东西;而项集一般是人为定义的某些商品的集合,比如我想要挖掘尿布和啤酒的关系,我就定义一个项集其中包含尿布和啤酒两项。
-
对于一个项集 \(X\),事务集中包含 \(X\) 的个数就叫做 \(X\) 的 支持度 \(\sigma (X)\),若 \(\sigma (X)\) 超过了某个阈值,则称 \(X\) 为 频繁项集。
强关联规则定义:
-
对于两个不相交的项集 \(X,Y\ (X \cap Y=\empty)\),用 \(X\to Y\) 表示一个关联规则,其中 \(X\) 记作前件,\(Y\) 记作后件;
-
关联规则 \(X\to Y\) 的支持度 support \(s(X\to Y)=\frac{\sigma(X\cup Y)}{N}=P(X\cup Y)\);
- 关联规则 \(X\to Y\) 的置信度 confidence \(c(X\to Y)=\frac{\sigma(X\cup Y)}{\sigma(X)} = P(Y\ |\ X)\);
- 若 \(X \to Y\) 的支持度 \(s\) 和置信度 \(c\) 同时超过了对应的阈值,则称 \(X \to Y\) 是一个 强关联规则。
关联分析的任务:
-
在给定事务集、支持度阈值和置信度阈值的情况下,找到所有的强关联规则。
-
显然可以直接枚举 \(X\to Y\) 的所有关联规则然后进行支持度检测和置信度检测。对于一个含有 d 个项的事务集,可能的关联规则总数为:
\[ 3^d - 2^{d+1} + 1 \] -
上式可以通过组合数学得来,就不说了。显然,指数复杂度是不能接受的,并且同时符合支持度阈值和置信度阈值的关联规则很少,很多计算都是无效的。
-
尝试优化。不难发现,对于一个强关联规则 \(X \to Y\),项集 \(\{X,Y\}\) 一定是一个频繁项集。也就是说我们可以先进行支持度检测找到所有的频繁项集,接着对于每一个频繁项集,将其中的项划分到前后件进行置信度检测。这样就可以更快速的挖掘出所有的强关联规则。(这种优化策略可以通俗的理解为:原本的暴力方法就是 n 层 for loop,现在使用一个 set 来维护 n/2 层 for loop 的计算结果,然后再用 n/2 层 for loop 来计算 set 中的信息)。
下面按照优化的思路,分别介绍支持度检测算法和置信度检测算法。
3.2 支持度检测¶
下面分别介绍三种支持度检测算法来寻找事务集中所有的频繁项集。
Apriori 算法¶
1)先验知识
一个频繁项集的子集一定也是频繁项集,一个非频繁项集的超集也一定是非频繁项集。
2)算法流程
- 扫描一遍事务集得到频繁 1 项集;
- 利用频繁 1 项集产生候选 2 项集;
- 在第二步产生的候选项集中通过支持度阈值筛选出频繁项集;
- 重复二、三直到找不到频繁 k 项集,结束循环。
3)算法核心
该算法的核心就在二、三两步。下面分别介绍:
-
对于第二步,需要利用「频繁 \(k\) 项集」产生「候选 \(k+1\) 项集」。可以通过以下两步来加速产生过程,具体的:
-
连接步。双重 for loop 寻找匹配的两个 \(k\) 频繁项集并连接产生一个候选 \(k+1\) 项集,这里的匹配指的是这两个 \(k\) 频繁项集「有 \(k-1\) 项是相同的且有 \(1\) 项是不相同的」;
-
剪枝步。在连接步得到所有的候选 \(k+1\) 项集后,并不是直接就到第三步的支持度计数了,这里还可以进行剪枝,即过滤掉一部分的候选 \(k+1\) 项集。而剪枝方法就可以用到一开始提到的先验知识「一个非频繁项集的超集也一定是非频繁项集」,即如果当前候选 \(k+1\) 项集中包含了非频繁 \(k\) 项集,那么它就不可能是频繁 \(k+1\) 项集。因此我们可以检查当前候选 \(k+1\) 项集中所有的 \(k\) 项子集是否都存在于频繁 \(k\) 项集中,只要有一个子集不存在,那么当前的候选 \(k+1\) 项集就不可能是频繁的,直接删除即可。(其实都挺显然的,只不过用语言描述起来挺费劲)
-
-
对于第三步,需要利用支持度阈值从「候选 \(k+1\) 项集」中筛选出「频繁 \(k+1\) 项集」。有两种方法可以加速支持度计数的过程,具体的:
- 基于事务树。可以在一开始利用完整的事务集维护一个「项集计数字典列表」,例如
List[ Dict[str, int] ]。后续在对候选 k+1 项集进行支持度计数时,只需要取出List[k+1]这个字典(其中维护了事务集中所有 \(k+1\) 项集的支持度计数的数值,这里假设项集可以用一个 str 来唯一表示),然后接近 \(O(1)\) 的累加字典中的数值即可。这种方法适用于事务集不变以及一个项集可以用一个可哈希的 key 来表示的情况; - 基于哈希树。这与事务树是逆过程,事务树是先维护事务,然后遍历候选项集进行支持度计数;而哈希树的思路是,基于每一轮产生的候选项集维护一棵树,然后遍历事务集进行支持度计数。感觉这种方法不如上一种方法来的巧妙。
- 基于事务树。可以在一开始利用完整的事务集维护一个「项集计数字典列表」,例如
4)时间复杂度分析
支持度阈值越小、事务集的项数越多、事务集的事务数越多、事务集中的事务平均宽度越大,Aprioir 算法的时间复杂度就越高。
5)频繁项集的紧凑表示
需要注意的是,由于计算置信度时需要使用之前计算过的支持度信息,当频繁项集很多时,这会造成很大的存储消耗,为了减少这种存储消耗,我们需要减少频繁项集的数量,为此引入「极大频繁项集」和「闭频繁项集」来压缩频繁项集的数量从而在保留重要信息的前提下减少存储消耗。具体的:
- 极大频繁项集。是指这样的频繁项集,它的所有的直接超集都不是频繁项集。给出了判断项集频繁性的最简表示但损失了频繁项集的支持度计数信息;
- 闭频繁项集。是指这样的频繁项集,它的所有的直接超集都不具有和它相同的支持度计数。保留了频繁项集的所有信息但需要更多的存储资源。
FP-growth 算法¶
频繁模式增长 (Frequent-Pattern growth, FP-growth) 算法
主要分为两步,一步是构造 FP 树,一步就是根据 FP 树寻找频繁项集。举例说明:假设最小支持度阈值为 22.2%(2/9)。
一)构造 FP 树
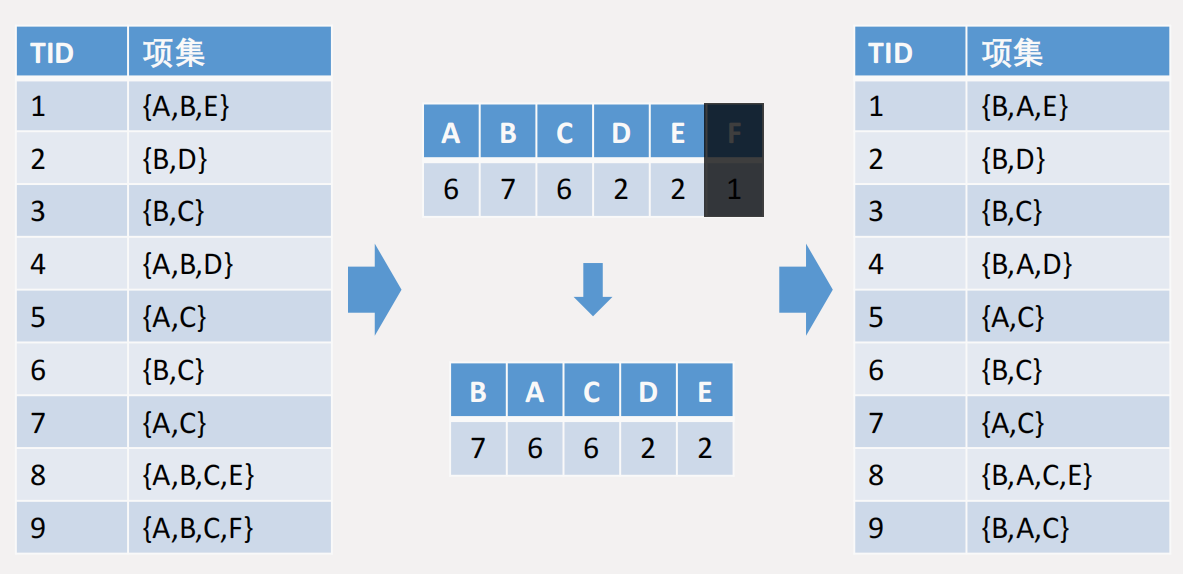
首先扫描一遍事务集,去除不符合最小支持度阈值的项 F,并将频繁项按照频率降序排序,同时对每一个事务中的项按照频繁项的顺序重新排序,如下图所示:
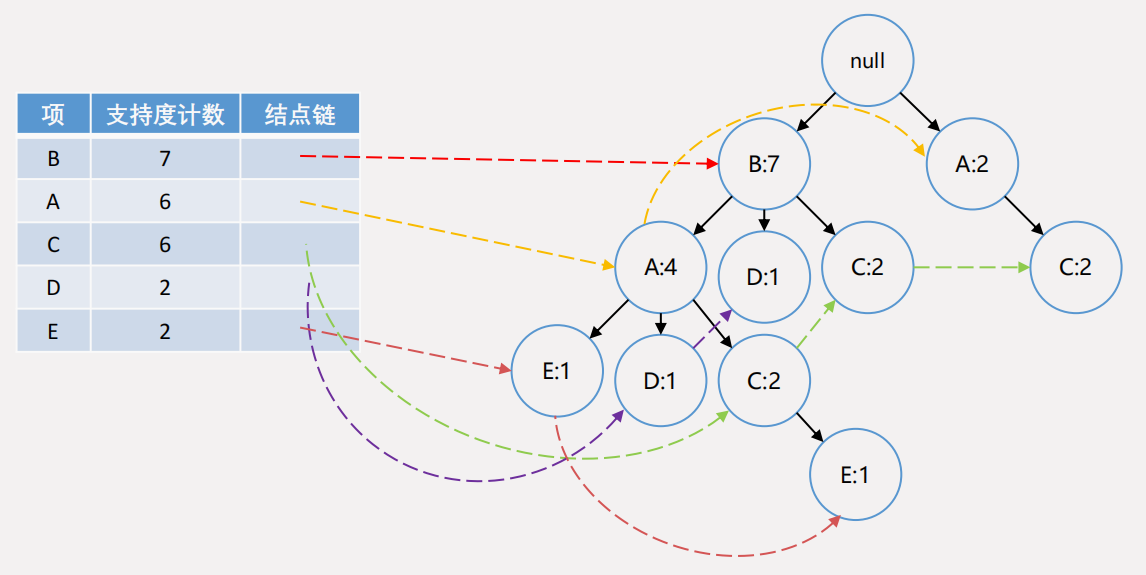
接着再扫描一遍事务集构造出最终的 FP 树,如下图所示:
2)寻找频繁项集
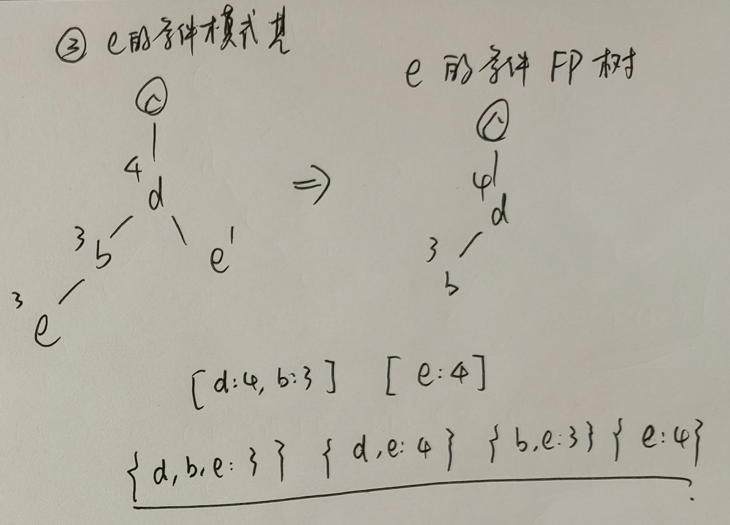
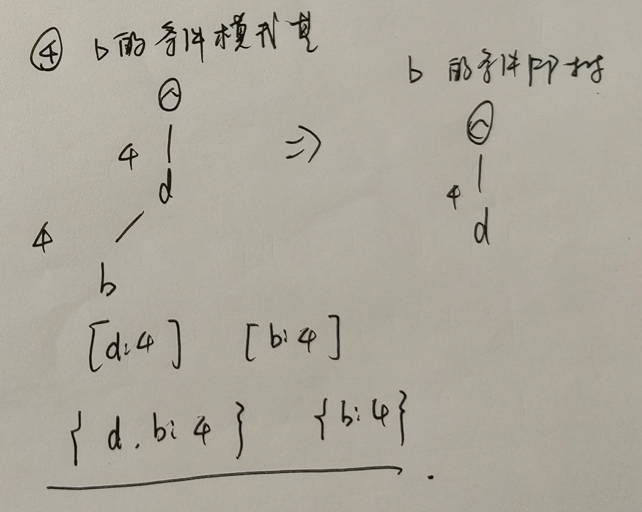
构造完 FP 树后,如何基于该树寻找频繁项集呢?分为三步:
- 基于 FP 树构造每一个频繁项的条件模式基 (conditional pattern base)。简而言之就是 以频繁项为叶子结点的子树;
- 基于条件模式基构造条件 FP 树 (conditional FP tree)。简而言之就是 条件模式基去掉叶子结点的子树;
- 基于条件 FP 树寻找频繁项集。寻找方法就是 对前后缀模式进行排列组合,最终项的数量需要取最小值。
当然,第一步中的排序规则并不是一定要按照频率降序排序的,不同的排序方式会导致不同的建树结果同时对于后续寻找频繁项集也是不确定的,这导致了 FP-growth 算法的不稳定性。
例题
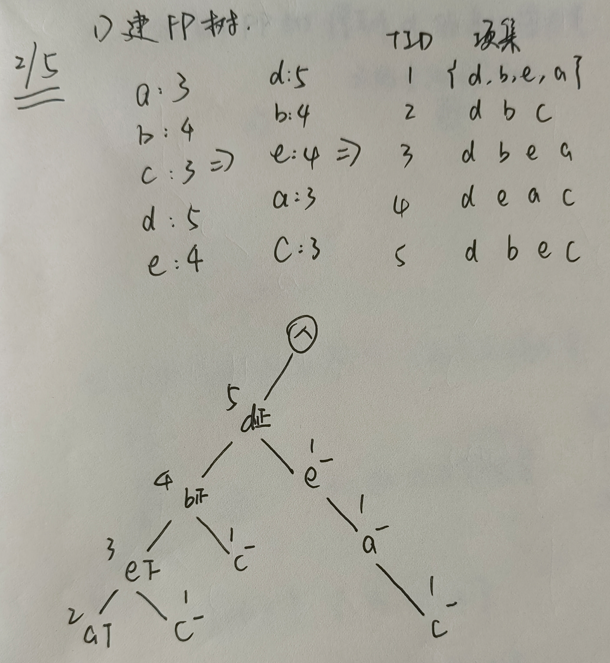
假设现在的最小支持度阈值为 40%,按照下面的事务集,使用 FP-growth 算法寻找出所有的频繁项集:
| TID | 项集 |
|---|---|
| 1 | {a,b,d,e} |
| 2 | {b,c,d} |
| 3 | {a,b,d,e} |
| 4 | {a,c,d,e} |
| 5 | {b,c,d,e} |
1)构建 FP 树
首先扫描一遍事务集得到所有频繁项并对事务集中的项进行排序,然后基于重排的事务集构建 FP 树:
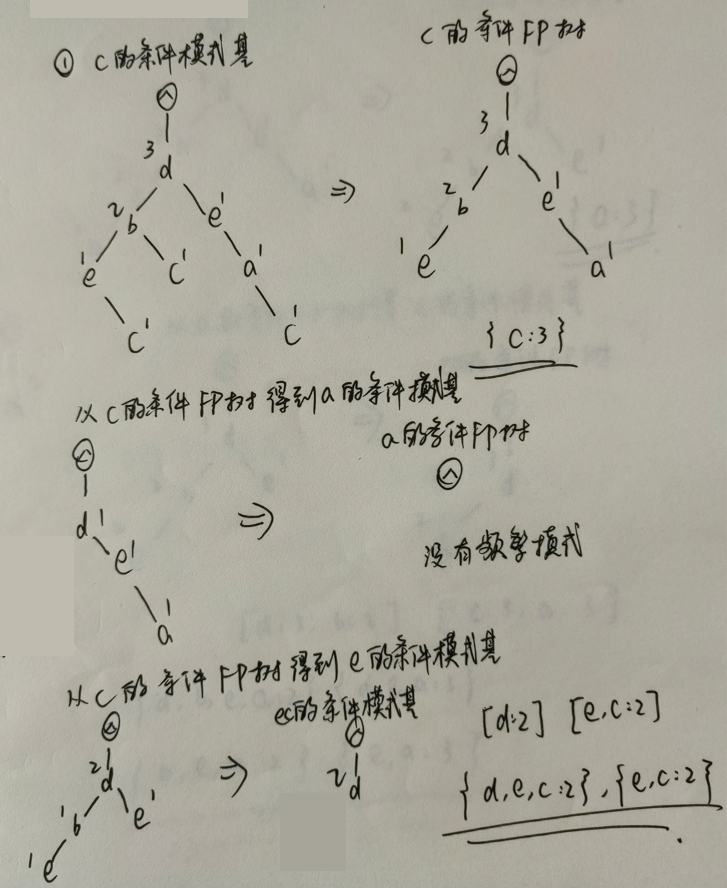
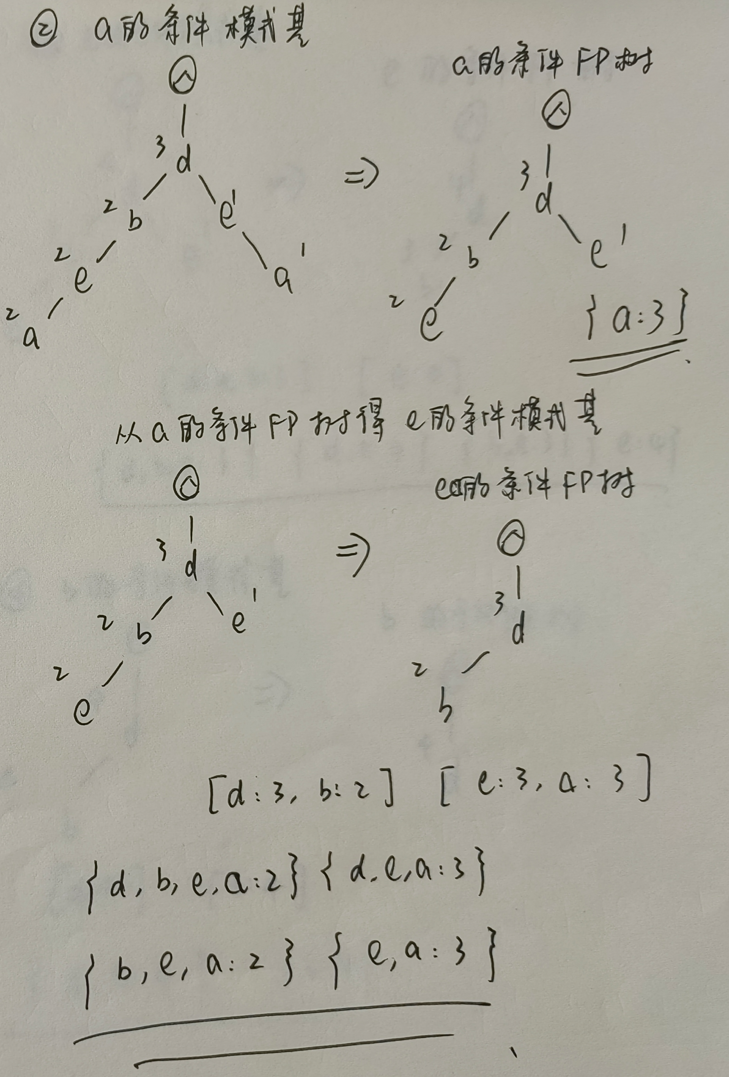
2)寻找频繁项集
以 c 为频繁项:
以 a 为频繁项:
以 e 作为频繁项:
以 b 作为频繁项:
以 d 作为频繁项:
Eclat 算法¶
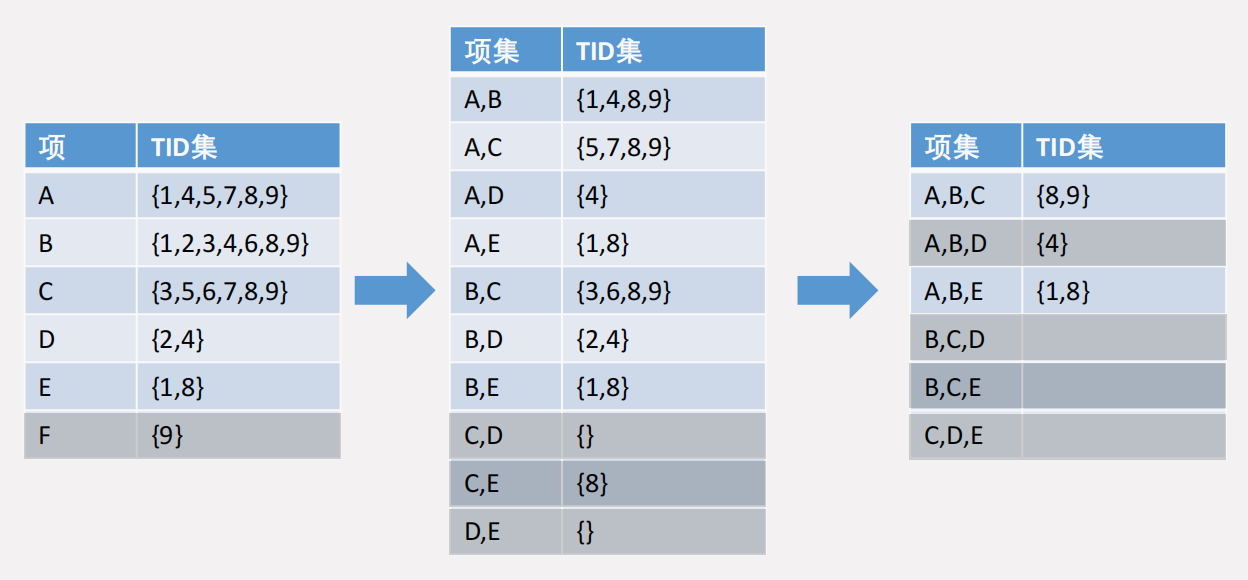
等价类变换(Equivalence CLAss Transformation,Eclat)算法
这里再补充一个 Apriori 算法的变种,叫做 Eclat 算法。其算法逻辑是将项集编号和项集进行「反拉链」存储:
后续在统计频繁项集时只需要取 TID集 的交集即可:
3.3 置信度检测¶
有了所有的频繁项集,接下来就是在每一个频繁项集中挖掘强关联规则。具体的,假设当前的一个频繁项集为 \(F\),且 \(|F|=k\),那么就可以枚举 \(2^k-2\) 次所有的前后件组合进行置信度检测。由于前面在计算支持度时,频繁项集中所有的项都算过支持度了,就可以提前保存好供当前置信度检测时使用,因此置信度检测时除了 \(O(2^k)\) 的枚举开销之外,其余时间开销可以看做 \(O(1)\)。
当然,我们在进行前后件组合的搜索时,可以利用先验知识进行剪枝。具体的,假设当前的频繁项集 \(F\) 被划分为了 \(X \to F-X\) 的关联规则:
- 若关联规则 \(X \to F-X\) 不满足置信度检测,则 \(X' \to F-X\) 也一定不满足置信度检测。其中 \(X'\) 为 \(X\) 的子集;
- 若关联规则 \(X \to F-X\) 满足置信度检测,则 \(X \to (F-X)'\) 也一定满足置信度检测,其中 \((F-X)'\) 为 \(F-X\) 的子集。
上面两个先验知识利用置信度检测的式子就可以一目了然的推出来。
3.4 更强的强关联规则定义¶
仅仅使用支持度和置信度仍然有可能挖掘出没那么有意义的关联规则,例如对于一个在支持度置信度框架下挖掘出的强关联规则,有可能是因为其中的前件或者后件的单独销量很高而误判了。为了解决这个问题,基于「支持度、置信度和相关性」三个准则的强关联规则的定义被提了出来。也就是说,还需要满足相关性的阈值标准才能被称为强关联规则。
1)提升度
对于两个项集 \(X\) 和 \(Y\):
- 如果 \(\frac{P(X\bigcup Y) }{P(X)P(Y)} >1\) 则说明 \(X\) 和 \(Y\) 是正相关的,这也是我们进行关联分析所感兴趣的;
- 如果 \(\frac{P(X\bigcup Y) }{P(X)P(Y)} = 1\) 则说明 \(X\) 和 \(Y\) 是相互独立的,没有研究意义;
- 如果 \(\frac{P(X\bigcup Y) }{P(X)P(Y)} < 1\) 则说明 \(X\) 和 \(Y\) 是负相关的,其中一项的出现会抑制另一项的出现,也没有研究意义。
2)杠杆度
这是提升度的另一种表现,三种关系很显然,就不说了。
3)全置信度
4)最大置信度
5)Kulc 度量
6)余弦度量
注:上述 6 种相关性度量标准中第一种以 1 为界,第二种以 0 为界,后四种以 0.5 为界。并且都是越大越相关。
零不变性。即度量数值不随零事务的变化而变化,所谓零事务就是不包含任何项的事务。说白了,就是度量的规则不受那些无关事务的影响,上述 6 种度量规则中后四种都具有零不变性。根本原因是表达式中的量纲没有发生改变。
不平衡比。从零不变性可以看出后四种是更为合理的相关性度量准则,因此我们将目光聚焦在后四个度量标准上,可以看出无非就是对 \(P(X|Y)\) 和 \(P(Y|X)\) 进行运算。定义不平衡比:
也就是 \(X\) 发生概率与 \(Y\) 发生概率之差比上 \(X\) 或 \(Y\) 发生的概率。IR 越大表示数据集越不平衡。实验的结论是:当数据不平衡时,可以综合使用 Kluc 度量和 IR 度量。
3.5 关联分析在序列数据上的应用¶
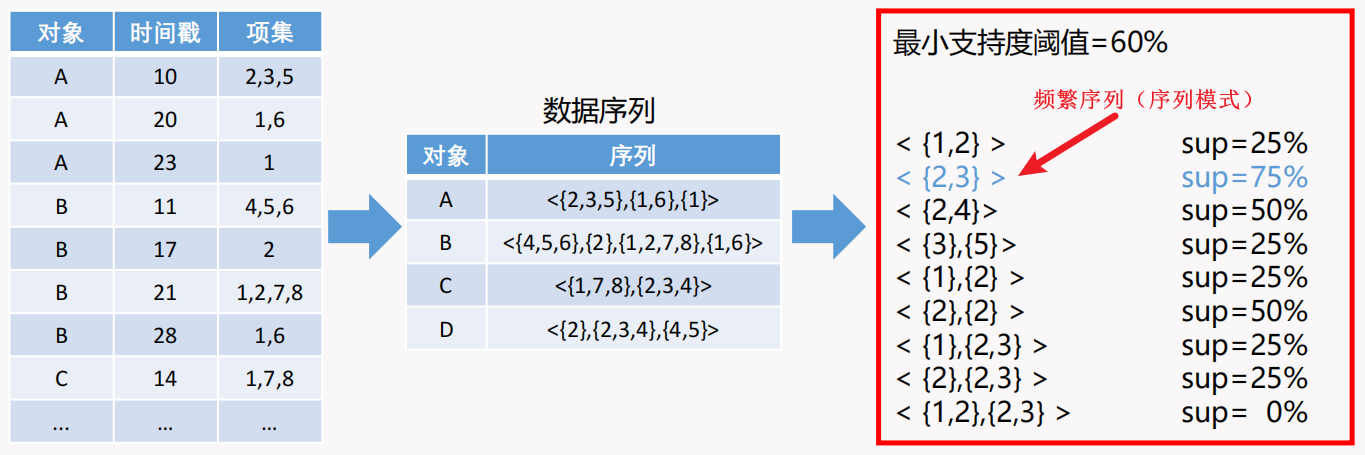
当数据的类型不是非对称的二元属性,而是一个序列数据时,如何挖掘其中的强关联序列呢?本节我们补充学习子序列的包含关系、频繁序列(序列模式)的表示形式以及「k-序列」的定义。
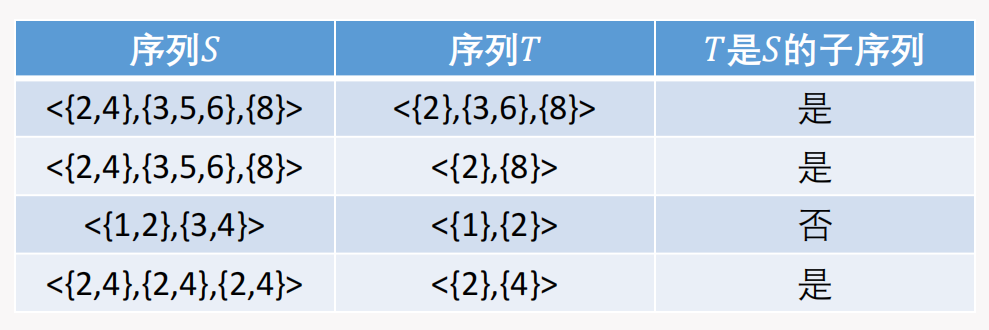
子序列的包含关系如下图所示:
频繁序列(序列模式)的定义为满足最小支持度技术的序列,如下图所示:
k-序列即包含 \(k\) 个项的序列,序列中的元素可以重复,例如对于一个只有两个项的 2-序列,可以有以下的所有序列可能:
4 聚类问题¶
本章我们继续学习一个老生常谈的问题:聚类。笔记会在之前的一篇博客上进行补充。重点学习以下三种聚类策略:
5 异常检测¶
异常检测也可以称为离群点检测,主要用来检测出离群点。但是这里的异常检测和 chapter2.1 数据清理并非一回事。
- 在非异常检测的任务中,通常将噪声和离群点当做一个东西来处理掉;
- 而在异常检测的任务中,需要对两者进行区分,并且异常检测的任务就是检测出离群点。
因为离群点的出现可能预示着数据中含有不同的分布情况,这通常是让人感兴趣的,而噪声无论是什么任务都需要提前处理掉。
5.1 基本概念¶
在异常检测任务中,数据往往都没有进行标注;并且由于异常数据的比例极少,这也导致了数据不平衡的问题;与此同时,由于异常数据的特征是没有定义的,很容易就将其和噪声混淆了。
由于上述的种种限制,使得异常检测任务很难使用二分类器进行拟合;并且也无法使用有监督学习方法,往往只能使用无监督学习的方法来进行异常检测。
异常点的类型主要有以下三种:
- 全局离群点。即可以通过邻近性度量直接区分开;
- 情境离群点。在某种情境下,需要一定的先验知识,例如检测地区温度异常,需要考虑到地区的差异带来的温度差异,而不是仅仅考虑一个温度的数值差异;
- 集体离群点。同样需要先验知识,需要知道不同数据群体之间的邻近性度量的差异。
5.2 异常检测算法¶
孤立森林¶
孤立森林 (Isolation Forest) 是一个基于集成树模型的「无监督」异常检测算法。对于森林中的每一棵树,初始时含有所有的数据对象,每次对树的所有结点进行分裂,分裂规则为随机选择一个属性并随机选择一个分割点,然后基于这个分割点将结点中的数据对象划分为两部分,直到一个结点只含有一个数据对象或者达到最大深度时停止分裂。孤立森林中树之间的区别取决于分裂时选择的属性不同,这与决策树算法比较类似。
森林构造出来的,如何确定异常点呢?该算法定义第 \(i\) 个样本 \(x_i\) 的异常分数 \(s\) 为下式:
其中:
- \(c(N)\) 表示数据集大小为 \(N\) 时每一个样本的平均路径长度;
- \(E(h(x_i))\) 表示样本点 \(x_i\) 在所有树中的平均路径长度。
评判标准:
- 异常分数越接近 \(1\) 就表明当前样本点越有可能是异常点。因为此时样本点的平均路径很短,说明当前样本点很容易就被区分开了;
- 异常分数越接近 \(0\) 就越不可能是异常点。说明当前样本点在所有集成树上的平均路径很长,很难和别的样本区分开;
- 若数据集中样本点的异常分数都接近 \(0.5\) 就说明当前数据集没有异常点。说明数据集中的所有样本都很类似。
算法分析:
-
优点:计算效率更高;
-
缺点:不适用于高维稀疏的样本分布。难以发现集体离群点。
基于距离的异常检测¶
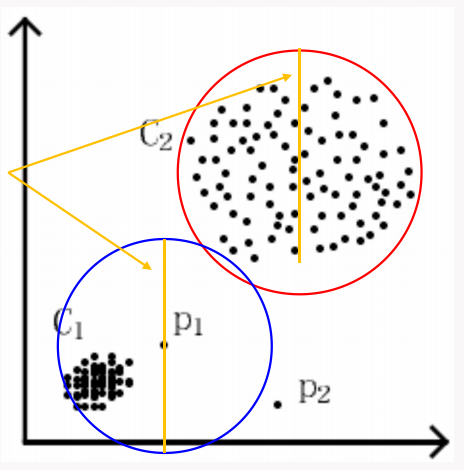
一句话概括就是如果一个数据对象的 \(r\) 邻域内数据对象个数不足阈值 \(k\),则认为当前数据对象是一个异常点。代码实现时,双重 for loop 即可。
该法有一个很大的问题就是,超参数有两个,很容易出现不同超参导致聚类结果大幅波动的问题。比如下面的数据分布:
数据对象 \(P_1\) 邻域内的对象数量是满足阈值的,但是很容易看出来 \(P_1\) 是一个异常点。
基于密度的异常检测¶
基于密度的异常检测就可以规避上述基于距离的异常检测隐含的问题。这里介绍 LOF 算法,论文地址为:LOF: Identifying Density-Based Local Outliers
定义数据对象 \(x\) 的「k-距离 \(dist_k(x)\)」为全体数据对象中与其相距第 k 大的距离值。定义 \(N_k(x)\) 为全体数据对象中距离数据对象 \(x\) 的距离小于等于 k-距离的数据对象个数。于是可以得到以下两个指标:
-
数据对象 \(x\) 的局部可达密度 (local reachable density):
\[ lrd_k = \frac{|N_k(x)|}{|N_k(x)| \times dist_k(x)} = \frac{1}{dist_k(x)} \]Tip
我对上式做了简化。在原始的式子中,分母是当前数据对象 \(x\) 的邻域内所有数据对象 \(x'\) 的可达距离之和。可达距离定义为 \(\max{(dist_k(x), dist(x, x'))}\),显然的邻域内数据对象 \(x'\) 到当前对象 \(x\) 的可达距离全都是 \(dist_k(x)\),因此可以简化为上式。
-
数据对象 \(x\) 的局部离群点因子 (Local Outlier Factor):
\[ LOF_k = \frac{\sum_{x'\in N_k(x)} \frac{lrd_k(x')}{lrd_k(x)} }{|N_k(x)|} \]
其中:
- 当 LOF 接近 1 时说明当前点和邻近点的密度相似,可能是正常点;
- 当 LOF 小于 1 时说明当前点的密度比邻近点更大,可能是簇中心;
- 当 LOF 远大于 1 时说明当前点的密度远小于邻近点的密度,可能是离群点。
说白了,就是给出了每一个数据对象的密度度量标准,然后看看邻域内点的密度和当前点的密度差异,就可以检测异常点了(至于为什么这么定义,鬼知道。反正在数据集上测出来的点数很高就行了,樂!)。
6 分类问题¶
本章主要学习分类算法来解决分类问题,这其实都和机器学习的课程内容了,具体的知识点见之前的笔记。重点学习以下内容:
决策树模型:决策树模型。
集成学习:集成学习。
分类任务的度量指标(重点关注二分类):性能度量。