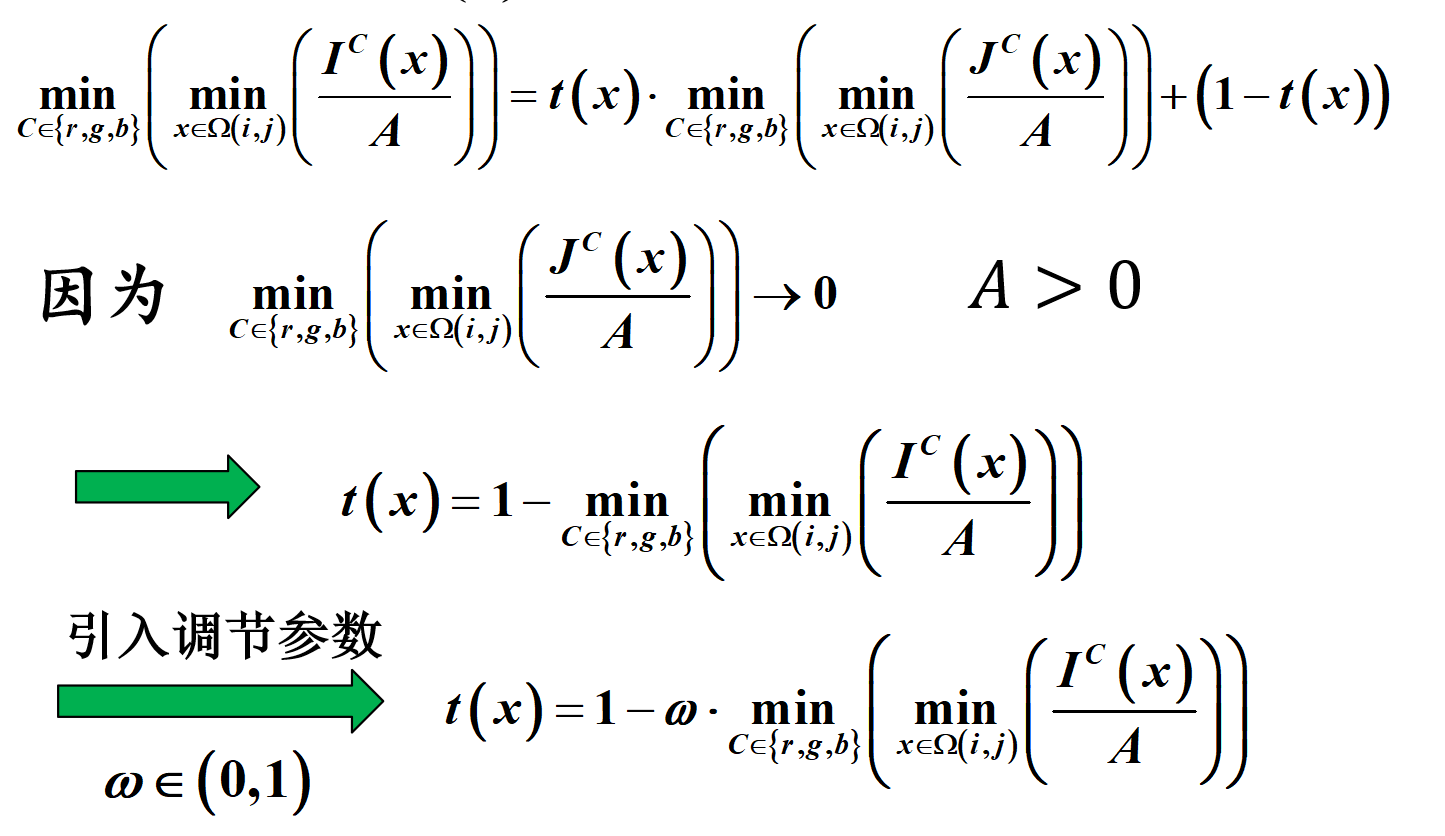数字图像处理
前言¶
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN 号 |
|---|---|---|---|---|---|
| 数字图像处理 | 《数字图像处理 使用 MATLAB 分析与实现》 | 2 | 蔡利梅 王利娟 | 清华大学出版社 | 9787302654100 |
| - | 《智能图像处理 Python 和 OpenCV 实现》 | 1 | 赵云龙 葛广英 | 机械工业出版社 | 9787111694038 |
为什么要学这门课?
图像是数据的一种,图像的应用场景极为广泛,因此如何获取、处理、存储数据也就显得十分重要。在本课程中我们将主要学习图像的处理技术。当然,如果非要说数字图像处理和别的课程的关联,愚以为既然图像是数据,那么就可以用到数据算法那一套上,也就与别的课程有了关联。
会收获什么?
图像简单来说就是一个矩阵。如何在这种数据结构上进行理论研究与算法应用显得十分有学习意义。本课程也将使用 MATLAB 和 OpenCV-Python 进行编码实现。
注:
本课程的代码分为 MATLAB 和 OpenCV-Python。其中:
图像获取¶
颜色空间
RGB、HSI(色调、饱和度、强度)、HSV(色调、饱和度、明度)。
模拟图像数字化
由于现实世界中的模拟图像是连续的,而计算机无法处理连续数据,因此我们只能对模拟图像进行采样并量化(离散化)。进而引出了下面的一些概念。
-
像素。一张模拟图像被离散化后的最小单元;
-
分辨率。一张模拟图像被离散化后的像素数量。例如,如果一张模拟图像被划分为由 \(2560\times1920\) 个像素点组成的数字图像,那么这张数字图像的分辨率就是像素点的数量,约 500 万;
-
在单一变量原则的情况下,分辨率越高,数字图像就越清晰吗?并不是。由分辨率的定义,一张图像的分辨率表示图像中像素点的个数。如果 A, B 两张图的分辨率一致,但是 A 图的面积远超过 B,那么显然的 B 比 A 更清晰。因为 A 的一像素对应的信息量太多了,不够精细,也就导致 A 更模糊。因此我们引出了图像清晰度的度量理念;
-
图像清晰度的定义。从上面的分析可知,图像的清晰度不是由像素的数量决定的,而是由 像素的密度 决定的。于是引出了以下两种像素密度度量方式:
-
PPI 用于描述显示设备(如显示器、手机屏幕等)的分辨率(注:下面的屏幕尺寸是指屏幕对角线的长度):
\[ \text{PPI} = \frac{\sqrt{(\text{水平像素数})^2 + (\text{垂直像素数})^2}}{\text{屏幕尺寸(英寸)}} \] -
DPI 用于描述打印设备(如打印机)的分辨率:
\[ \text{DPI} = \frac{\text{打印的点数}}{\text{每英寸的距离}} \]
-
数字图像的类型
介绍三种,分别是二值图像、灰度图像和彩色图像:
- 二值图像中,每一个像素点就是 \(0\) 或 \(1\);
- 灰度图像中,每一个像素点取值在 \([0,255]\) 之间;
- 彩色图像中每一个像素点是一个三通道向量,\(R,G,B\) 的取值均在 \([0,255]\) 之间。
MATLAB 的数字图像基本操作
颜色互换
图像类型互换
图像的读取、显示与保存
图像编码 *¶
这一部分本课程不作要求,但愚以为这是十分重要的一个部分。
承接上一部分的「图像获取」技术。现在我们有了图像数据,就需要对其进行传输和存储,但是图像的数据量极大,如果不进行压缩编码,必将在传输和存储的过程中造成极大的消耗,因此图像的压缩编码是很重要的。目前主要有两种压缩编码策略,分别是 无损压缩编码 和 有损压缩编码。
图像处理¶
有了图像数据,我们就可以进行最基本、最底层语义的图像处理,进而才能有后续更高语义上的 图像分析 和 图像理解。这一部分我们将从图像的各个处理策略入手,分别进行学习。
1 图像基本运算¶
1.1 基本原理¶
首先需要掌握一些最基本的概念:齐次坐标表示与变换矩阵 \(T\)、图像插值策略、图像映射策略。以及关于坐标系的注意点。
关于齐次坐标表示和变换矩阵。就是将图像中的点 \((x,y)^T\) 用 \((x,y,1)^T\) 来表示。之所以要这样表示,从 这篇博客 可以看出是为了「统一图像变换的运算形式」,但应该没这么简单,可能还有很多别的意义。至于所谓的变换矩阵,其实就是利用矩阵乘法对图像的像素点转换进行运算格式上的统一,所有的变换操作都可以统一为对像素点的矩阵乘法,例如:对于当前的一个像素点 \(p=(x,y,1)^T\) 和一个变换矩阵 \(\displaystyle \begin{bmatrix} k_x & b & \Delta x \\ c & k_y &\Delta y \\ p & q & s \end{bmatrix}\)。新像素点 \(p'=(x',y',1)^T\) 可以通过矩阵乘法 \(p'_{3\times 1}=T_{3\times 3} \times p_{3\times 1}\) 得到,即:
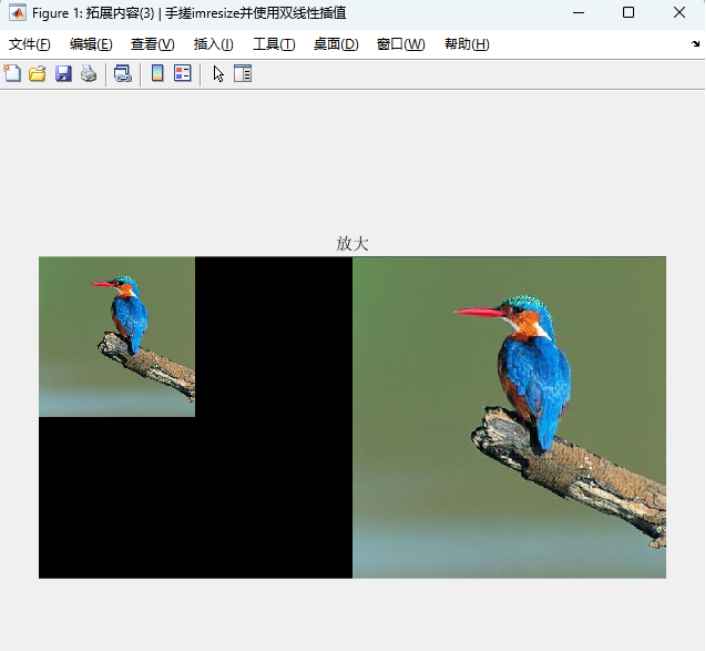
关于图像插值策略。常用的有三种,分别是最邻近差值、双线性插值、双三次插值。其中最邻近插值很显然,双三次插值最精准但是计算量很大,因此最常用的还是双线性插值。
关于图像映射策略。有前向映射法和后向映射法,常用的是后向映射法,因此讲讲后向映射法的流程。逻辑很简单,根据原图像的「四个顶点」与「几何变换逻辑」确定新图像的位置后,基于几何变换的 逆变换 逐个填充新图像的像素值即可。填充策略也很显然,当我们对新图像的像素点使用逆变换寻找在原图像的对应点时,会发生以下两种情况:
- 新图像在原图像的对应点超过了原图像的范围。说明这个像素点是由于几何变换而凭空出现的,直接赋背景色即可。
- 新图像在原图像的对应点没超过原图像的范围。说明这个像素点一定是有实际意义的,此时又有两种情况:
- 对应点存在的。说明找到了「最佳配对」,这是最完美的对应情况,直接赋原图的像素值即可;
- 对应点不存在。说明没有最佳配对,此时我们只能退而求其次给这个像素点生成一个配对的像素值,怎么生成呢?就可以用到上面介绍的插值策略了。
关于坐标系。理论计算和编程实现是不同的:
- 理论计算时。采用的是 像素坐标系,左上角为原点。\(A(x,y)\) 中,\(x\) 表示在 \(\rightarrow\) 方向的投影,\(y\) 表示在 \(\downarrow\) 方向的投影。
- 编程实现时。采用的是 矩阵坐标系,左上角为原点。\(A(x,y)\) 中,\(x\) 表示在 \(\downarrow\) 方向的投影,\(y\) 表示在 \(\rightarrow\) 方向的投影。
1.2 几何变换¶
主要有平移、镜像、旋转、缩放和错切 5 种变换。下面利用后向映射法详解旋转的逻辑,然后基于这套逻辑实现缩放的底层代码。其余的几何变换操作类似,就不再赘述,掌握编程语言的 API 即可。
Note
我们以图像的左上角即原点作为旋转点,逆时针方向为正方向。对于原图中的任意点 \((x, y)\),我们将其表示为 \((r\cdot \cos \alpha,r\cdot \sin \alpha)\),逆时针旋转 \(\theta\) 度后,就有下面的变换公式和逆变换公式。
变换公式(在老点的坐标系下,已知老点算新点):
逆变换公式(在新点的坐标系下,已知新点算老点):
确定新图尺寸。我们可以利用上述变换公式,首先「在原图的坐标系下」计算出 4 个顶点变换后的坐标 \(P_1(x_1,y_1),P_2(x_2,y_2),P_3(x_3,y_3),P_4(x_4,y_4)\) 来确定新图的尺寸:
坐标系转换。与平移/镜像时可以直接使用逆变换找老点时不同,旋转时的坐标系会发生变化(其实就是新原点相对于老原点在 \(x\) 和 \(y\) 方向上有了一定的偏移量),因此我们需要 先将新点逆偏移到老点的坐标系中,再根据逆变换寻找到对应的老点。逆偏移的逻辑很简单,对于新图中的任意一点 \((x', y')\),逆偏移的计算方法如下:
坐标逆变换。最后我们进行坐标逆变换辅以合理的插值策略即可实现后向映射法。
结果如下:
Warning
下面用 maketform 构造出来的变换矩阵是理论变换矩阵 \(T\) 的转置结果 \(T'\)。
1.3 代数与卷积运算¶
关于代数运算。分为代数运算(加减乘除)和逻辑运算(与或非),都很显然,不再赘述。
关于卷积运算。就是滑动窗口,在数字图像中都是二维的滑动窗口。关于边缘像素的填充方法,有以下几种:赋零不扩边;复制不扩边;赋零扩边;复制扩边。都很显然,不再赘述。
1.4 正交变换 *¶
上面学习的内容都是对图像在「空间域」上进行的运算,现在我们对图像进行变换得到「频域」信息,从而可以在频域上的对图像进行变换与分析。
图像中可以被人类识别的数据在频域上都是低频,而一些例如噪声、边缘信息在频域上都是高频。因此通过「高通」或「低通」等滤波器可以对图像从频域上进行过滤操作。
傅里叶变换原本是连续函数的变换方法,在计算机处理时需要进行离散化处理。因此我们需要掌握离散傅里叶变换。对于一个 \(n\) 维向量,离散傅里叶变换的时间复杂度是 \(O(n^2)\),为了加速这个变换过程,基于分治的快速傅里叶变换被设计了出来,使得变换的时间复杂度优化到了 \(O(n\log n)\)。
补充一下 卷积定理。空间域的乘积等价于频域的卷积,空间域的卷积等价于频域的乘积。
2 图像增强¶
图像增强是一个很大的门类,包含了下面的 [chapter4 图像去噪]、[chapter5 图像锐化] 等等。本章要介绍的图像增强是一个狭义的概念,主要是在讲如何「提升图像对比度」,也就是如何提升图像中明暗区域的差异程度。
注意:在灰度图像中,亮度取决于灰度值。例如在 256 级灰度图像中 \([0,255]\) 就对应从黑到白。
2.1 基于灰度级变换¶
灰度级变换的本质就是通过某种「函数映射关系」将灰度图像的像素值变换到其他的数值,从而实现灰度图像的对比度增强。常见的映射策略分为线性和非线性变换。具体的:
-
对于线性变换:
-
分段线性变换。不同的灰度级区域进行不同程度的线性变换,例如低灰度区域线性变换的斜率大于 1,高灰度区域线性变换的斜率小于 1;
-
高低端不变线性变换。即只对图像的中间取值范围内的灰度进行线性变换;
-
截取式线性变换。在高低端不变线性变换的基础之上,将高低端的像素值设置为两个定值。MATLAB 例程如下:
-
-
对于非线性变换:
- 对数变换。提亮;
- 指数变换。变暗;
- 幂次变换。\(\gamma\in(0,1)\) 时与对数变换类似,提亮;\(\gamma\in(1,\infty)\) 时与指数变换类似,变暗。
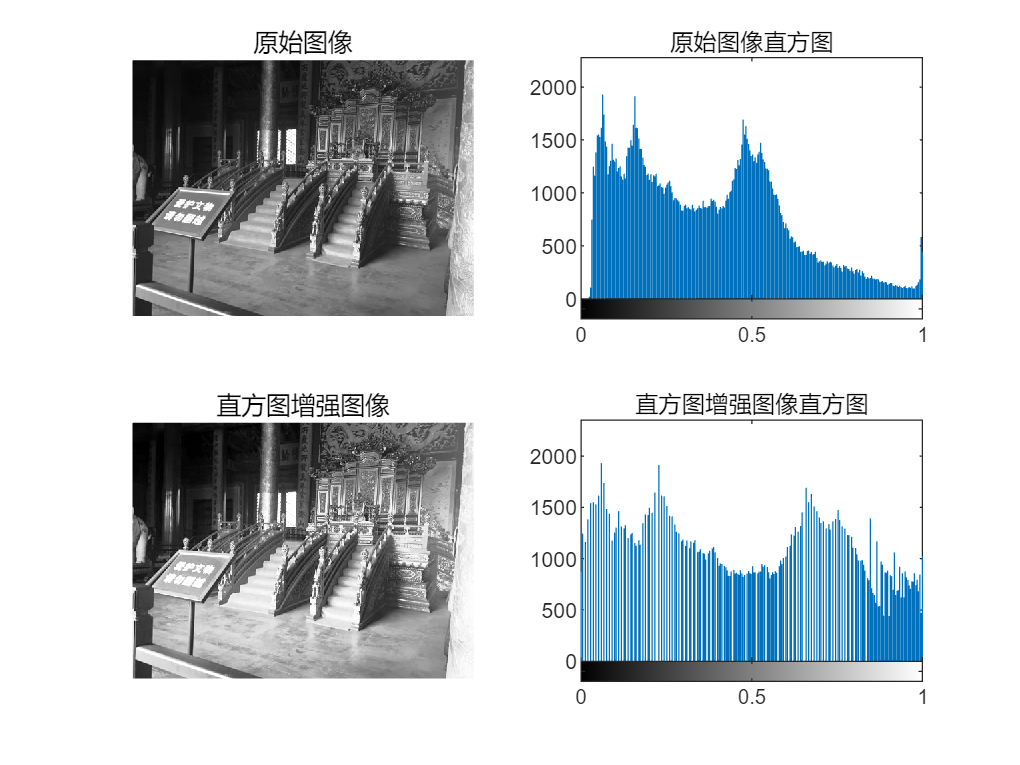
2.2 基于直方图修正¶
当一张灰度图像在每一个灰度级上的像素点数量均匀分布时,该灰度图像的信息量达到了最大,也就最清晰,直方图修正理论正是基于该理论进行的。而算法原理本质上还是找到一个映射关系将原图第 \(x\) 级的所有像素点全部映射到新图的第 \(y\) 级像素点,那么这个映射关系应该怎么寻找呢?为了方便,首先对图像的像素值进行归一化。
算法的设计者很巧妙的利用了灰度值概率的累积分布这一个物理量。具体的,对于原图 \(r\) 的第 \(x\) 级像素点,如果需要均匀分布的话,那么这一级的像素点理论上应该全部属于第 \(\displaystyle\left[\sum_{i=0}^x p(r_i) \right]\) 级像素点上。这里的中括号表示数值取到近邻的灰度级上。
比如说,现在的灰度级为 \(8\),那么归一化后的灰度级分布就是 \((0/7,1/7,\cdots,7/7)\),原图第 \(0\) 级的最优累计量应该就是 \(1/8\),但是呢如果说原图过曝了,像素值普遍很大,第 \(0\) 级的累计分布量是 0.47,那么就需要将所有第 \(0\) 级的像素点映射到第 \([0.47]=3/7\) 级像素点上。
很巧妙的一个函数映射!调用 MATLAB 的 API 例程如下:
2.3 基于照度反射模型¶
从「图像成像 \(f(x,y)\) 是由照射光强 \(i(x,y)\) 在物体上经过反射强度 \(r(x,y)\) 形成的」的角度通过变换对图像进行增强。其中 \(f(x,y)=i(x,y)\times r(x,y)\)。理解起来很容易,照射光强相对平稳,而反射强度会因为物体表面的信息变化很大。因此基于照度反射模型的图像增强逻辑就是衰减图像低频段,增强图像高频段。有两种方法可以基于照度反射模型进行增强:
-
基于同态滤波。本质就是一个高通滤波运算。对其 1)取对数之后拆分将积式转换为和式,2)利用傅里叶变换将和式转换为低频信息与高频信息之和,3)进而可以使用高通滤波器的卷积运算进行增强,最后再 4)逆变换到空间域并 5)取指数即可进行得到最终的图像增强结果;(注:根据卷积定理,上述 2,3,4 步的卷积运算可以直接用空间域的乘积来代替)
-
基于 Retinex 理论。先利用卷积直接计算出每一个通道的光照强度 \(i(x,y)\) 估计值,然后根据定义式取对数再作差即可。
2.4 基于暗原色先验¶
参见何凯明 [CVPR 2009] 的研究内容,主要讲的是针对雾天图片的对比度增强算法。
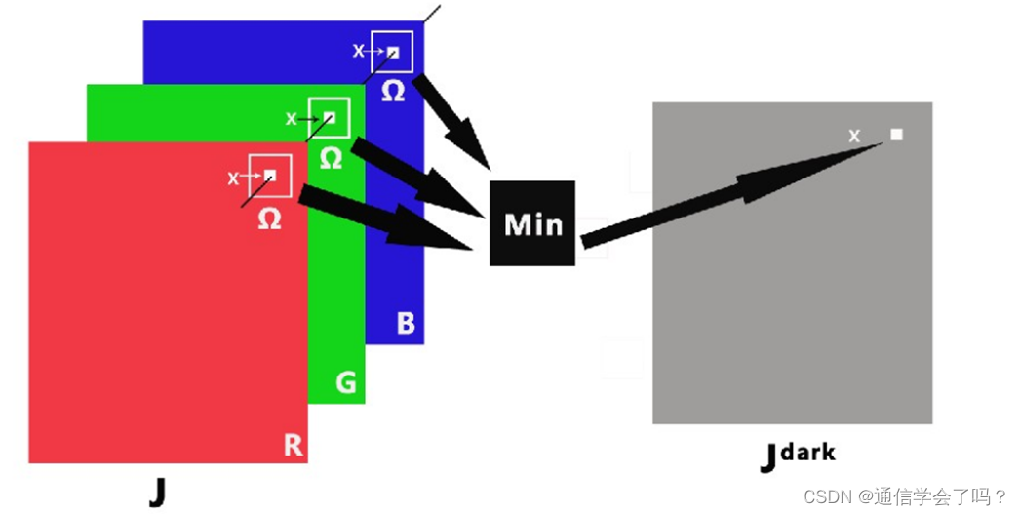
首先给出 暗原色先验原理。在无雾的环境下,绝大多数非天空图像的局部区域内,某一些像素在 RGB 三色通道中至少有一个通道的像素颜色值比较低。那么对于原始图像 \(J\),就可以计算出其每一个位置的暗原色灰度值从而得到暗原色通道图 \(J^{dark}\)。下图直观的给出了暗原色通道图的计算方法:
接着给出 雾天成像模型。定义图像中的某个像素点为 \(x\),雾天成像图为 \(I\),原始图像为 \(J\),成像像素点 \(x\) 距实体距离为 \(d(x)\),大气光为 \(A\),大气散射系数为 \(\beta\),则透射率 \(t(x)=e^{-\beta \cdot d(x)}\)。
与照度反射模型类似,如果是无雾的天气,那么「物体的反射光」可以被成像器较好的捕捉到,而雾天,空气中含有大量的雾介质,这增强了光的透射性,使得大量的大气光经过透射也被成像器捕捉到了。也就是说,雾天图像的本质就是「物体的反射光」和「大气光」经过透射后累加的结果。则有如下的雾天成像模型:
现在我们的问题转化为了求解 \(A\) 和 \(t(x)\) 两个参数值:
-
对于参数 \(A\),即大气光强度。由于雾天成像结果中含有大量大气光的透射结果,使得图像的暗原色通道值普遍较高,暗通道中灰度值较大的区域也就对应了雾天图像中最不透明的区域(因为这些区域几乎都是大气光透射的结果),那么此时的暗原色通道值就可以作为大气光强度 \(A\) 的估计值;
-
对于参数 \(t(x)\)。如下图估计:
有了参数 \(A\) 和 \(t(x)\) 的具体结果,就可以直接算出原始图像,也就是去雾图像了。
应用拓展。去雾的本质就是对亮度过高的图像进行增强,因此该算法对于过曝图像也可以处理;同样的,对于低光过暗的图像,可以先对其取反转化为过曝图像,然后应用去雾算法进行处理,最后再取反即可。
3 图像平滑¶
图像平滑也叫做「图像去噪」,属于图像增强的一种。一般可以从空间域和频域两个角度进行平滑。
在物体成像并被捕捉到成像器的过程中,如果遇到了现实世界的恶劣天气,很有可能产生噪声。同时,在不同介质之间传输图像时,也可能遇到传输错误导致图像产生了噪声。为了减弱噪声对图像呈现效果的影响,我们对图像噪声进行建模,将其建模成「高斯噪声」和「椒盐噪声」两类噪声模型。
3.1 均值滤波¶
所谓均值滤波,其实就是对原图使用「全 1 的卷积核」进行卷积运算。邻域越大,在消除噪声的同时也会让图像更模糊。
3.2 高斯滤波¶
所谓高斯滤波,对于二维图像,其实就是对原图使用「二维高斯分布的卷积核」进行卷积运算。此法 适用于高斯型噪声 场景。对于输出图像的 p 位置像素,卷积核中 q 位置的权重为:
当噪声符合高斯分布并且均值为 0 时,高斯滤波可以完美消除噪声。但是与均值滤波类似,\(\sigma\) 越大,邻域内的平均程度就越厉害,也就会导致图像越模糊。
3.3 中值滤波¶
所谓中值滤波,其实就是将原图中的每一个像素点用「邻域中像素中位数点」进行代替。此法 适用于椒盐型噪声 场景。
3.4 双边滤波¶
上面三个平滑策略仅仅考虑了像素的位置信息,但是忽略了像素的变化量信息,这就导致了上述三个算法如果将卷积核增大,就会导致平滑后的图像越来越模糊,丢失了图像的边缘信息和细节信息。为了解决这个问题,双边滤波策略被提了出来。所谓的双边滤波,其实就是既考虑像素的位置信息,又考虑了像素的变化量信息。其实就是在高斯滤波的卷积核进行了修改。双边滤波的输出值 \(I_p\) 是输入图像 \(I\) 在像素 \(p\) 处的平滑结果,计算公式如下:
可以发现卷积核中每一个位置的权重系数从高斯滤波的 \(G_s(\|p - q\|)\) 变成了 \(G_s(\|p-q\|) G_r(|I_p - I_q|)\)。也可以理解为增加了一个惩罚系数。
3.5 代码实现¶
下列代码参考:
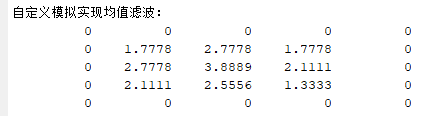
完整「均值滤波」代码实现
题目要求
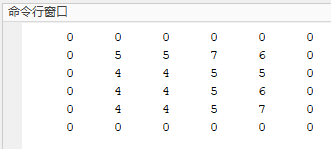
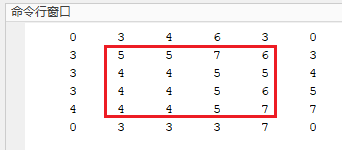
给定一张灰度图像 \(\displaystyle \begin{bmatrix} { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 5 } & { 1 } & { 6 } & { 0 } \\ { 0 } & { 4 } & { 6 } & { 3 } & { 0 } \\ { 0 } & { 7 } & { 2 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \end{bmatrix}\),使用 \(3\times 3\) 规格的均值滤波,不处理边缘像素。
理论分析
均值滤波可以通过使用全 1 的卷积核进行卷积运算来实现。即:
代码实现
1)matlab 自定义实现
输出:
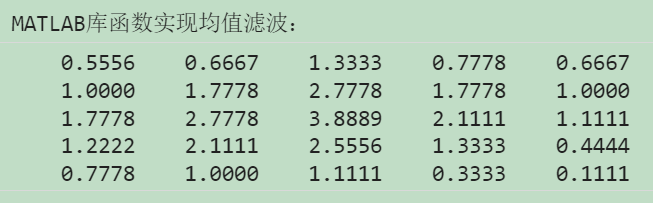
2)matlab 库函数
输出:
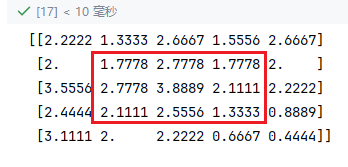
3)Python-OpenCV 库函数
输出:
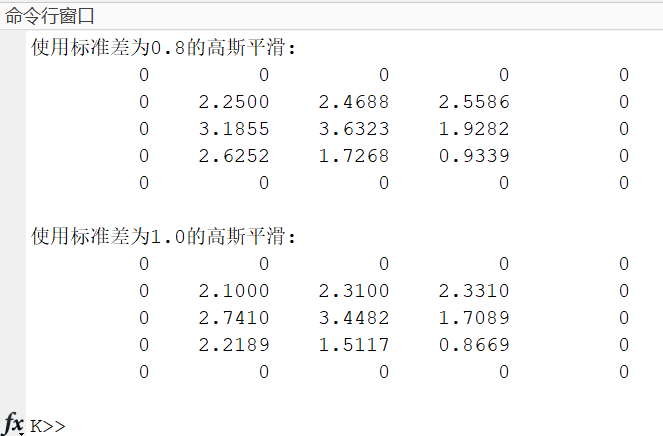
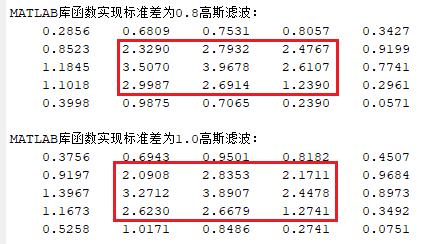
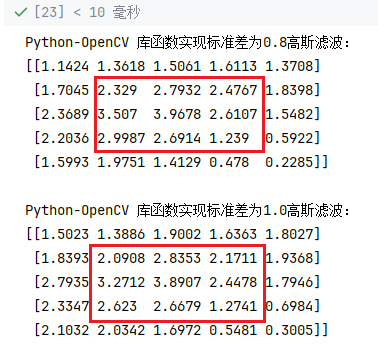
完整「高斯滤波」代码实现
题目要求
给定的一张灰度图像 \(\displaystyle \begin{bmatrix} { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 5 } & { 1 } & { 6 } & { 0 } \\ { 0 } & { 4 } & { 6 } & { 3 } & { 0 } \\ { 0 } & { 7 } & { 2 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \end{bmatrix}\),使用 \(3\times 3\) 规格的高斯滤波,标准差分别为 \(\sigma=0.8,\sigma=1\),不处理边缘像素。
理论分析
高斯滤波可以通过使用服从二维高斯分布的卷积核进行卷积运算来实现。
-
当 \(\sigma=0.8\) 时,卷积核参数为:
\[ \frac{1}{16} \begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 2\\ 1 & 2 & 1 \end{bmatrix} \] -
当 \(\sigma=1\) 时,卷积核参数为:
\[ \frac{1}{10} \begin{bmatrix} 1 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 1 \end{bmatrix} \]
代码实现
1)matlab 自定义实现
输出:
2)matlab 库函数
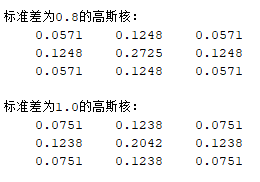
输出:同样只需要关注中间 9 个元素:
至于为什么和模拟的输出结果不一致,是因为自定义实现的代码中「高斯核参数并不完全准确」,matlab 中的高斯核参数如下:
3)Python-OpenCV 库函数
输出:
完整「中值滤波」代码实现
题目要求
给定一张灰度图像 \(\begin{bmatrix} 1 & 3 & 6 & 8 & 6 & 3 \\ 15 & 4 & 7 & 9 & 8 & 1 \\ 13 & 3 & 5 & 5 & 7 & 4 \\ 3 & 4 & 0 & 2 & 5 & 7 \\ 6 & 12 & 3 & 6 & 9 & 7 \\ 9 & 11 & 3 & 11 & 14 & 13 \end{bmatrix}\),使用自定义的邻域进行中值滤波,不处理边缘像素。并从中说明中值滤波适合处理哪种类型的噪声。
理论分析
中值滤波就是将每一个像素用邻域内像素的中值进行代替实现。假设仍然使用 \(3\times 3\) 规格的邻域进行滤波。
代码实现
1)matlab 自定义实现
输出:
2)matlab 库函数
输出:除了边缘,其余内容与自定义实现的代码运行结果一致:
3)Python-OpenCV 库函数
输出:
小结
从中值滤波的结果可以看出,原始图像中坐标为 (5,2) 的 12,(4,3) 的 0 等极端值都被周围的中值替换掉了,从而实现了平滑。从这一点也可以看出中值平滑算法可以去除图像中「椒盐型」的噪声,即小范围内的极端值像素点。
3.6 频域滤波 *¶
本节不做要求,但是简单介绍一下。上面的种种策略都是从空间域的角度对图像进行平滑去噪,也可以从频域的角度进行。我们知道,当图像通过傅里叶变换转换到频域后,噪声由于和周围正常像素点差异较大,会导致频率很高,因此我们可以在图像傅里叶变换后的图像上做一个低通滤波来过滤掉高频的噪声。
频域去噪滤波的一般流程是:
4 图像锐化¶
所谓的图像锐化就是对图像进行「边缘增强」。常规的图像锐化策略是:计算原图 \(f(x,y)\) 每个点的边缘信息得到一个边缘图像 \(g(x,y)\),然后将得到的边缘图像与原图相加即可得到锐化后的图像。因此图像锐化的关键在于如何计算图像中的边缘信息,下面将从一阶和二阶两个角度计算图像的边缘信息。将卷积模板称作算子。
而对于边缘检测任务,其实就是将上述求出来的边缘图像 \(g(x,y)\) 进行一个二值化。
4.1 一阶算子¶
基于一阶算子计算边缘梯度时,都是分别在 \(x\) 和 \(y\) 方向按照某种卷积核 \(H_x, H_y\) 卷积后将绝对值相加。
1)梯度算子
对应的算子(卷积核):
2)roberts 算子
3)sobel 算子
4)prewitt 算子
4.2 二阶算子¶
下面介绍的图像锐化算子都利用到了图像的二阶梯度信息。
1)二阶梯度算子
二阶梯度算子也叫拉普拉斯 (laplacian) 算子。该算子计算图像梯度的核心思想就是计算每一个像素位置的二阶梯度差分值。具体的:
很容易得到对应的算子:
2)Log 算子
在提取图像的梯度信息之前,一般需要对其先进行去噪。我们定义二元高斯函数在 \((x,y)\) 处的函数值为 \(G(x,y)\),则有如下的图像锐化流程:
由于上式可以进行以下转化:
因此我们可以直接将去噪和提取梯度信息合并成一步,即利用「二维高斯函数的二阶梯度」和原始图像做卷积运算即可。其中二维高斯函数的二阶梯度 \(\nabla^2G(x,y)\) 为:
3)Canny 算子
与其叫它算子,不如称其为算法。具体的:
- 同样首先需要进行二维高斯滤波;
- 然后利用上述各种算子提取出边缘梯度信息;
- 接着对上一步提取出来的边缘梯度信息取局部最大值;
- 最后连接邻域内的局部最大值点得到最终的边缘信息。
4.3 代码实现¶
1)梯度信息
关于梯度信息。使用上述各种算子(卷积核)对原图进行卷积运算即可。当然如果不想写 for loop,可以借助 MATLAB 中的 imfilter(I, h) 函数来一步实现卷积运算,只需要向其传送卷积核 h 参数即可,这里的 h 可以自己写,也可以借助 fspecial() 函数一次性获得。例如:
其中算子方法有以下几种学过的并且也集成到 MATLAB 中的:
-
一阶算子
-
fspecial("sobel"); -
fspecial("prewitt")。
-
-
二阶算子
2)边缘检测
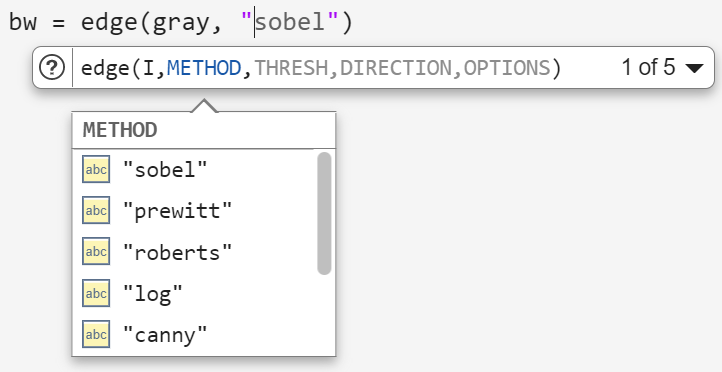
关于边缘检测。MATLAB 集成了边缘检测的算法,即 edge 函数。值得一提的是,这里的边缘检测结果其实就是对上述梯度信息进行二值化的结果,只不过这里的二值化阈值需要人为设定或者需要额外计算出一个阈值,这将会在 [chapter5.1 阈值分割] 中具体介绍。例如:
MATLAB 中集成了以下 5 种上面提到的算子方法:
4.4 频域滤波 *¶
与 [chapter3.6 频域滤波] 类似,提取图像边缘时也可以使用频域滤波。
从频域提取边缘图像的一般流程是:
5 图像分割¶
如何将图像中的对象(object)分割出来?
5.1 阈值分割¶
就是将给灰度图像设定一个阈值,不足阈值的就转为 \(0\),超过阈值的就转为 \(1\),从而得到一个二值化图像。这里最关键的就是阈值的人为设置。
1)直方图法
当图像中前景和背景比较纯净(占比较多)并且灰度分布相对集中时,灰度图像会呈现出双峰状态,将阈值取为峰谷对应的灰度值就可以实现较好的阈值分割。
当然并不是所有的灰度图像都符合上面的条件,导致直方图出现各种锯齿情况,此时就可以对其进行平滑。具体的,可以在直方图上动手脚,将相邻三个直方图对应的元素个数取均值作为中间的元素值,不断平滑直到可以找到一个相对合适的阈值。
2)模式分类法
阈值的定义域无非就是 \([0,255]\),而分割的本质就是将所有的像素点按照像素值进行二分类。如果我们可以基于像素的二分类结果建立一个度量指标,那么直接遍历阈值的定义域,最佳度量指标对应的阈值就是最终的阈值。基于这种思想,下面介绍三种模式分类策略:
最大类间方差 OTSU。顾名思义,就是让前景和背景两类像素值的方差最大。假设前景像素值的均值为 \(\mu_O\),前景像素点比例为 \(P_O\),背景像素值的均值为 \(\mu_B\),背景像素点比例为 \(P_B\),全局像素值的均值为 \(\mu\),那么类间方差,也就是度量指标定义为:
遍历找到使得该度量指标最大对应的阈值 \(T\) 作为最佳阈值即可。例程如下:
最大熵法。采用了信息论中的信息熵的概念。度量指标定义为:
同样的遍历找到使得该度量指标最大对应的阈值 \(T\) 作为最佳阈值即可;
最小误差法。该方法有一个强假设,即假设前景和后景的灰度频率分布都符合高斯分布,然后再建立一套度量指标。如下:
其中误差 \(\epsilon\) 定义为像素分错类别的概率,在一维高斯分布曲线中就是一个定积分。遍历找到使得该度量指标最小对应的阈值 \(T\) 作为最佳阈值即可;
5.2 边界分割¶
本节主要介绍边界检测的改良算法:Hough 变换法。通过检测出更精准的边界,从而实现对前景的提取与分割。
该算法的思想是:将笛卡尔积中的原始图像映射到极坐标系中的参数图像,那么原始图像中的一条线就对应了参数图像中的一个点,同样的参数图像中的一条线也对应了原始图像中的一个点。显然有这样的结论:原始图像中一条线段上每一个点映射到参数图像中的所有直线都会过参数空间中的同一个点 \((\theta_k, \rho_k)\)。
于是基于 Hough 变换的直线检测算法就呼之欲出了:
- 枚举原始图像 \(f(x,y)\) 中的像素点 \((x_i,y_i)\),结合 \(\rho = x \cos \theta + y \sin \theta\) 并尺取 \(\theta\),得到一组 \([\theta_i, \rho_i]\) 并将其在参数图像 \(p(\theta,\rho)\) 中进行桶计数(原始图像中的点映射到参数空间中的一条线)。hough;
- 假设原图中有 \(k\) 条线段,那么就取出参数图像中最大的 \(k\) 个点对应的坐标。houghpeaks;
- 参数空间中的这 \(k\) 个点坐标就对应了图像空间中的 \(k\) 条线段。houghlines。
基于这样的思想,使用 MATLAB 进行直线检测的例程如下:
5.3 聚类分割¶
将每一个像素点用一个向量表示特征后,就可以套上各种聚类算法。最简单的,K-means。对于 MATLAB 中的 K-means API:
图像分析¶
上述内容完成了对图像的各种增强,现在我们尝试从图像中进行更高语义的抽取,也就是所谓的特征提取。
6 图像描述与分析¶
边缘特征。局部二元模式 (Local Binary Pattern, LBP);
梯度方向特征。梯度方向直方图 (Histogram of Oriented Gradients, HOG)。具体的,将图像划分为一个个小的单元区域,然后用一个滑动窗口维护每一个区间内的梯度直方图统计信息,最后将每一个直方图向量统计信息按列拼接起来即可。也就是说每一张图像的梯度方向信息就是一个很长的行向量。
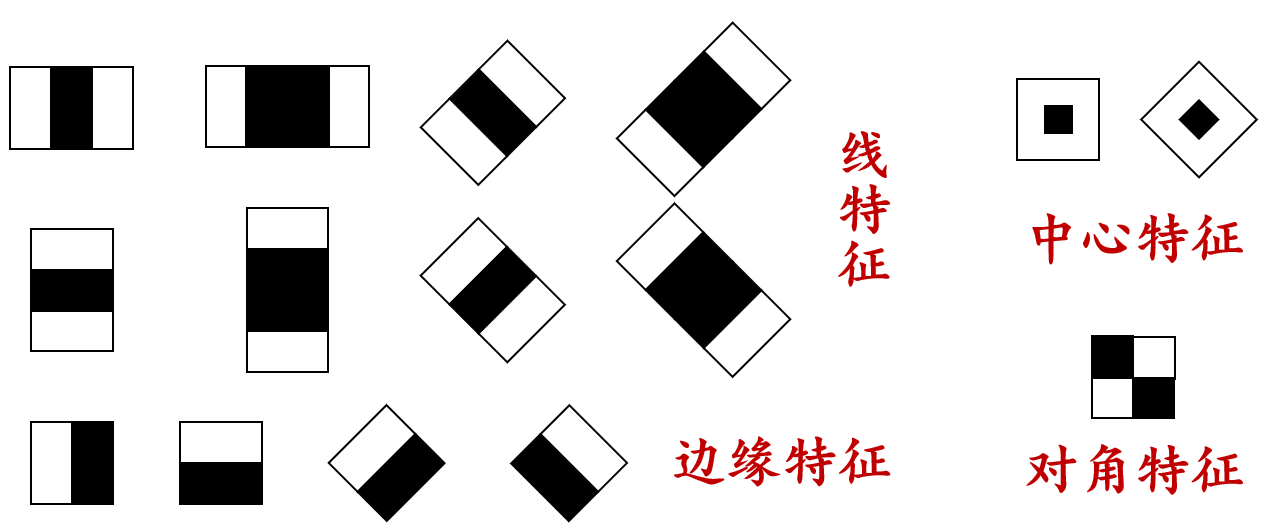
Haar-like 特征。可以通过区域像素值的差来提取图像中的各种特征,至于如何快速计算区域的像素差,可以使用二维前缀和的处理技巧进行加速。可提取的特征如下图所示: