高等数学导读
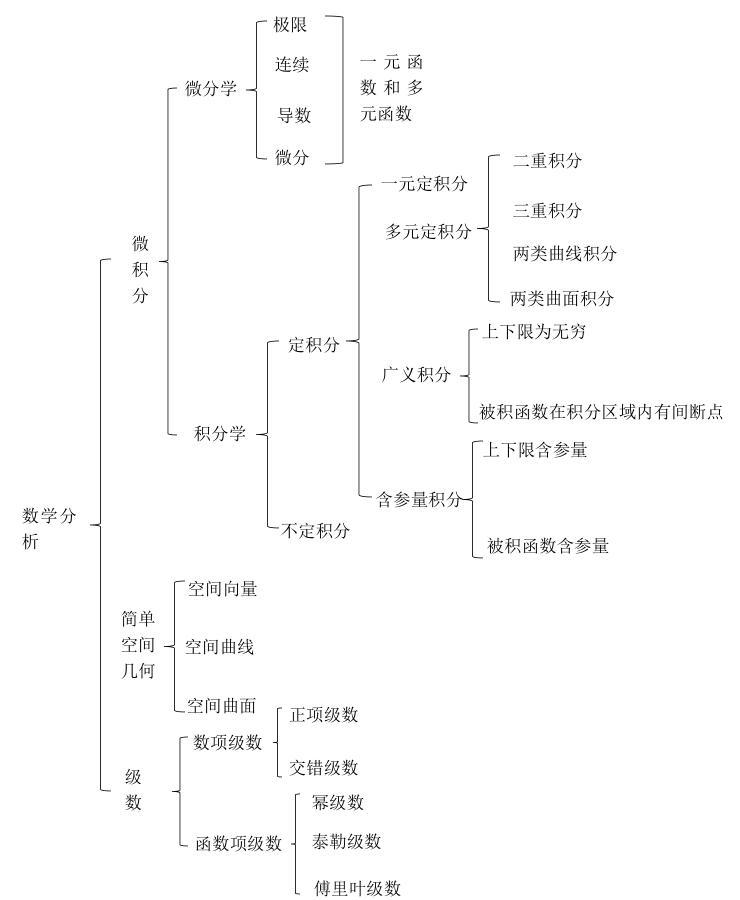
本文记录高等数学的学习笔记。由于笔记产生于大学生数竞 1 2 以及速成阶段 3,内容只涉及微积分。下图展示了数学分析(高等数学)的知识体系,感兴趣的小伙伴可以对本专栏进行补充。
图 1. 知识体系 4
| 概念 | 定义 | 数学表示 | 几何意义 | 计算方式 | 应用 |
|---|---|---|---|---|---|
| 导数 (Derivative) | 表示函数在某点的斜率 | \(f'(x) = \lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h}\) | 曲线在某点的切线斜率 | 直接对函数求导 | 速度、优化 |
| 偏导数 (Partial Derivative) | 多元函数对某个变量的变化率 | \(\dfrac{\partial f}{\partial x} = \lim\limits_{h \to 0} \dfrac{f(x+h, y) - f(x, y)}{h}\) | 某个变量方向上的切线斜率 | 对一个变量求导,其他变量视作常数 | 反向传播、物理建模 |
| 微分 (Differential) | 用导数近似函数的微小变化 | \(\mathrm d f = f'(x)\mathrm dx\) | 小范围内的线性近似 | 对变量偏导数并乘以变量的微小变化 | 误差估计 |
| 全微分 (Total Differential) | 多元函数在所有变量方向上的微小变化 | \(\mathrm d f = \dfrac{\partial f}{\partial x_1} \mathrm d x_1 + \dfrac{\partial f}{\partial x_2} \mathrm d x_2 + \dots + \dfrac{\partial f}{\partial x_n} \mathrm d x_n\) | 所有变量方向上的线性近似 | 对每个变量求偏导数并乘以对应变量的微小变化 | 多变量优化 |
| 差分 (Finite Difference) | 离散化的导数近似 | 前向差分:\(\dfrac{f(x+h) - f(x)}{h}\) | 离散点之间的变化率 | 计算有限步长 \(h\) 的差值 | 数值求解微分方程 |
| 积分 (Integral) | 求和运算 / 导数的逆运算 | \(\displaystyle \int f(x) dx\) | 求面积或累积量 | 计算反导数或求和 | 位移、能量 |
| 梯度 (Gradient) | 多元函数在各方向的变化率 | \(\nabla f = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y} \right)\) | 函数增长最快的方向 | 计算所有偏导数组成向量 | 梯度下降 |
表 1. 概念对比表
总结:
- 导数 vs. 偏导数:导数是一元函数的瞬时变化率,偏导数是多元函数对某个变量的变化率。
- 微分 vs. 差分:微分是导数的近似变化,差分是离散版的导数。
- 积分 vs. 导数:积分是导数的逆运算,表示累积量。
- 梯度 vs. 偏导数:梯度是所有偏导数组成的向量,表示函数增长最快的方向。