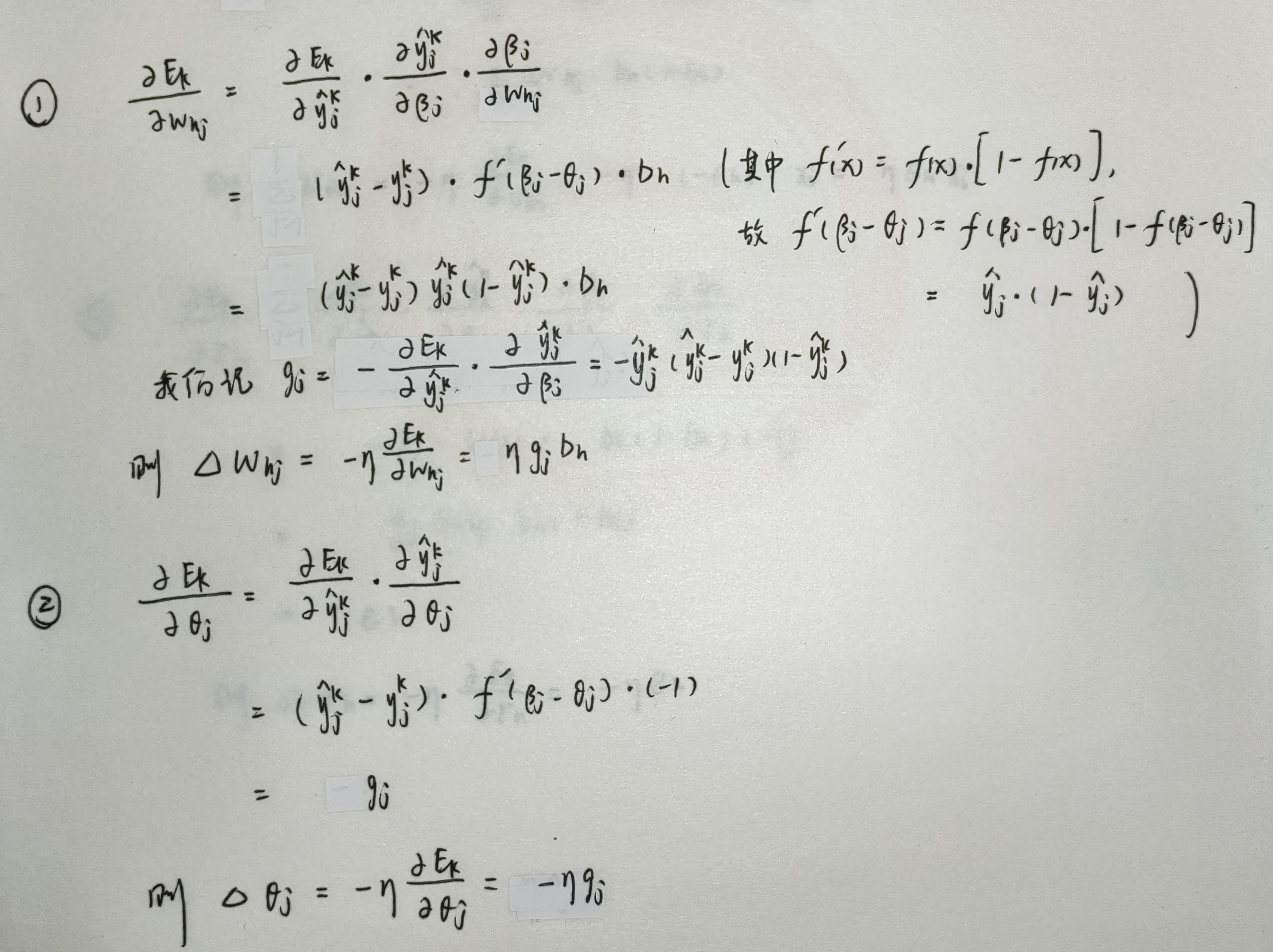跳转至

深度学习导读

本文记录深度学习入门笔记。教材主要参考邱锡鹏老师的 《神经网络与深度学习》 1，其余参考内容：

绪论

深度学习是什么？相较于机器学习中「手动提取特征」从而进行之后的下游任务，深度学习则直接规避了手动提取特征的人工干预，直接让模型自动提取数据特征并进行之后的下游任务，从而实现所谓「端到端」的任务范式。这里的自动提取特征也被叫做「表示学习」，具体流程如下图所示：

深度学习的数据处理流程

图 1. 深度学习的数据处理流程

为什么会有深度学习？最简单的一点就是，很多特征我们根本没法定义一种表示规则来提取，比如说对于图像，怎么定义复杂的图像的特征呢？比如说对于音频，又怎么定义复杂的音频的特征呢？没办法，我们直接学特征！

神经网络是什么？就是万千模型中的一种，给定输入，得到输出，仅此而已。

为什么用神经网络进行深度学习？有了上面对深度学习定义的理解，可以发现其中最具有挑战性的特点就是，模型怎么知道什么才是好特征？什么是不好的特征？神经网络可以很好的解决这个问题。通过由浅到深的层层神经元的特征提取，深层的神经元就可以学习到更高语义的特征，并且由于不同层级的神经元可以提取到不同层级的语义特征，也可以很好地解释深度学习中特征的「贡献度分配」问题。

全连接神经网络

全连接神经网络 (Full Connect Neural Network, FNN) 又称前馈神经网络 (Feedforward Neural Network)、感知机 (Perceptron)，是深度神经网络模型的开山鼻祖，通过向前传递数据，向后更新参数，实现学习和拟合的功能。

人工神经元

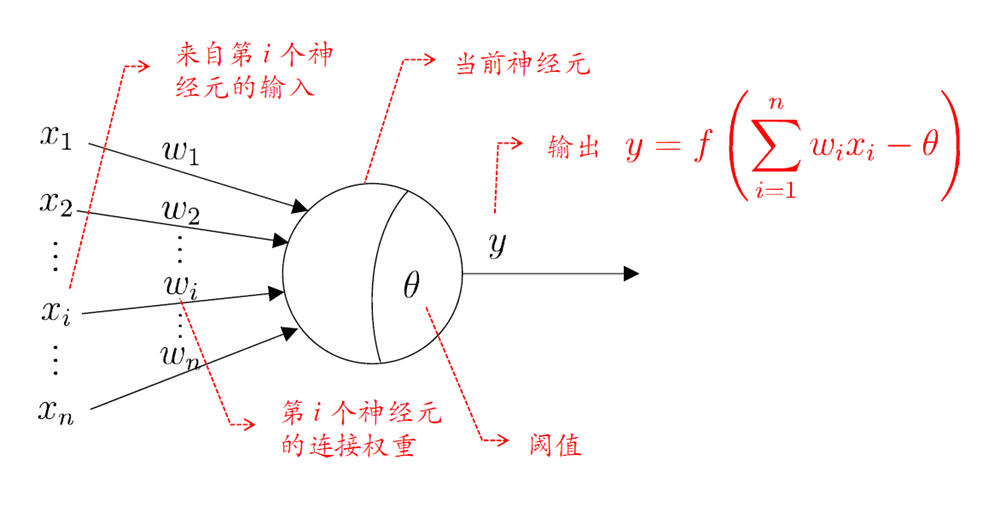
人工神经元模型

图 2. 人工神经元模型

神经元是网络模型中的最小学习单元。每一个神经元接受输入 \(\sum_{i=1}^n w_ix_i - \theta\)，通过设定好的激活函数 \(f\) 得到该神经元对应的输出值 \(f(\sum_{i=1}^n w_ix_i - \theta)\)。其中 \(\theta\) 可以理解为神经元的激活阈值，也可以理解为神经元模型中的偏置项。

神经元中的激活函数大有门道、种类极多。为了确保网络可以拟合复杂的映射关系，需要激活函数是「非线性」的；为了便于对网络求导从而进行参数更新，需要确保激活函数是「可导」的；为了防止对网络求导的过程中出现梯度消失或者梯度爆炸，需要确保激活函数是「单调并且有界」。主要有以下 3 种类型：

  • S 型函数。例如 Sigmoid 函数、Tanh 函数；
  • 斜坡函数。例如 ReLU 函数；
  • Swish 函数。复合函数。

FNN 模型

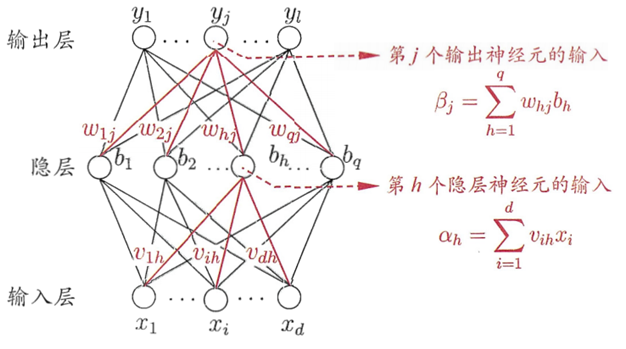
两层全连接神经网络

图 3. 两层全连接神经网络模型

Tip

在神经网络模型中，我们定义输入层为前，输出层为后。

功能简介。所谓全连接神经网络，就是各层神经元之间不会跨层连接，也不存在同层连接，其中：

  • 输入层仅仅接受外界输入，没有函数处理功能；
  • 隐藏层和输出层进行函数处理。

神经元的输入与输出。分为「有函数处理功能」和「无函数处理功能」两类：

  • 隐藏层：对于隐藏层的第 \(h\) 个神经元
  • 输入：\(\alpha_h = \sum_{i=1}^dx_i v_{ih}\)
  • 输出：\(b_h = f(\alpha_h - \gamma_h)\)
  • 输出层：对于输出层的第 \(j\) 个神经元
  • 输入：\(\beta_j=\sum_{h=1}^q b_h w_{hj}\)
  • 输出：\(\hat y_j = f(\beta j - \theta_j)\)

网络参数。现在给定一个训练集学习一个分类器。其中每一个样本都含有 \(d\) 个特征，\(l\) 个输出。每输入一个样本都迭代一次。对于单隐层神经网络而言，一共有 4 种参数，即：

  • 输入层到隐层的 \(d \times q\) 个权值 \(v_{ih}(i=1,2,\cdots,d,\ h=1,2,\cdots,q)\)
  • 隐层的 \(q\) 个神经元的阈值 \(\gamma_h(h=1,2,\cdots,q)\)
  • 隐层到输出层的 \(q\times l\) 个权值 \(w_{hj}(h=1,2,\cdots,q,\ j=1,2,\cdots,l)\)
  • 输出层的 \(l\) 个神经元的阈值 \(\theta_j(j=1,2,\cdots,l)\)

FNN 学习准则

假设每次输入一个训练样本进行参数更新（即 batch size = 1）。由于网络输出内容是实数，因此我们定义目标函数 \(\mathcal L\) 为当前训练样本的「均方误差」。那么对于第 \(k\) 个训练样本，就有如下损失：

\[ \mathcal L_k = \frac{1}{2} \sum _{j = 1}^l (\hat y_j^k - y_j^k)^2 \]

其中：为了求导方便，添加一个常量 \(\dfrac{1}{2}\)。\(\hat y\) 为样本真实值，\(y\) 为样本预测值。

FNN 优化算法

在进行梯度下降时，经过简单的推导可以发现，第 \(l\) 层的损失 \(\delta (l)\) 依赖于后一项的损失 \(\delta(l+1)\)，于是参数更新的逻辑就是从输出层开始逐层往后更新，直到第一层隐藏层。为此，我们引入著名的优化算法：误差逆传播算法 (error Back Propagation, BP)，其算法流程如下图所示：

误差逆传播算法流程

图 4. 误差逆传播算法流程

以上述单隐层神经网络为例，尝试推导参数更新的过程。假定学习率（搜索步长）为 \(\eta\)，那么上述 4 种参数的迭代公式就为：

\[ \begin{aligned} w_{hj} &\leftarrow w_{hj}+\Delta w_{hj} \\ \theta_{j} &\leftarrow \theta_{j}+\Delta \theta_{j} \\ v_{ih} &\leftarrow v_{ih}+\Delta v_{ih} \\ \gamma_{h} &\leftarrow \gamma_{h}+\Delta \gamma_{h} \\ \end{aligned} \]

其中，修正量分别为：

\[ \begin{aligned} \Delta w_{hj} &= \eta g_j b_h \\ \Delta \theta_{j} &= -\eta g_j \\ \Delta v_{ih} &= \eta e_h x_i \\ \Delta \gamma_{h} &= -\eta e_h \\ \end{aligned} \]
利用链式法则推导修正量

公式表示

公式表示

隐层到输出层的权重、输出神经元的阈值

隐层到输出层的权重、输出神经元的阈值

输入层到隐层的权重、隐层神经元的阈值

输入层到隐层的权重、隐层神经元的阈值

卷积神经网络

为了解决全连接网络「不能学习到局部不变性」以及「参数量过大」的缺点，卷积神经网络 (Convolutional Neural Network, CNN) 应运而生。卷积网络有三大特征：局部连接、权重共享、时/空上的次采样（汇聚/池化）。

卷积基本概念

统一表述。卷积是加权平均运算，属于线性运算。如果不对卷积核翻转，那么其实是叫「互相关」运算，真实的卷积是需要对卷积核翻转 180 度后再进行加权平均运算。为了统一：

  • 语言描述上：由于卷积网络中的卷积核是可学习的并且与是否翻转无关，为了统一表述，后文提到的卷积运算都指互相关运算，即不翻转的加权平均操作；
  • 符号表示上：理论上互相关运算记作 \(\otimes\)，卷积运算记作 \(*\)，后文统一用 \(\otimes\) 表示卷积运算。

基本术语。下面简单介绍一些在卷积神经网络中的术语：

  • 滤波器 (Filter) 与卷积核 (Convolutional Kernel, K) 概念一致，指的是同一个东西；
  • 特征映射 (Feature Map)：卷积运算后的结果，可以理解为卷积操作后提取出的特征；
  • 感受野 (Receptive Field)：神经元对原始输入的感受范围，越深的神经元感受野就越大；
  • 通道 (Channel, C)：在二维卷积中，通道数就是图像的深度，在一维卷积中（例如 NLP 任务），通道数就是词向量的维度；
  • 移动步长 (Stride, S)：卷积核在输入数据中每次移动的长度；
  • 零填充 (Zero Padding, P) 操作通过给输入数据的边缘填充 \(0\)，从而可以让输入数据的每一个位置之间被等价处理；
  • 卷积核大小记作 (Kernel Size, K)。

卷积方式。

  • 等宽卷积：通过零填充让输入与输出的大小相同；
  • 宽卷积：通过零填充让每个输入点参与卷积运算的次数相同；
  • 窄卷积：不做任何零填充操作。

CNN 模型

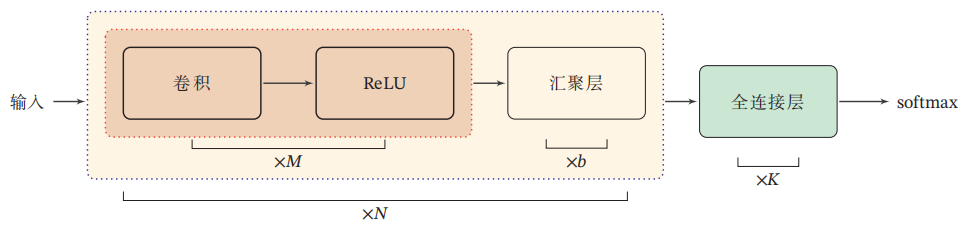
常用的卷积网络整体结构

图 5. 常用的卷积网络整体结构

卷积层。对于二维卷积而言，我们假设输入共有 D 个图像，需要学习 P 个特征，并不是只需要学习 P 个卷积核的，对于每一个特征需要单独对每一张图像学习一个卷积核，因此需要学习 \(D\times P\) 个卷积核。

汇聚/池化层。从上面的卷积层学习逻辑可以看出其实参数量和全连接层相比还是很大。池化层就是通过减小输出数据的尺寸来大幅降低参数量；通过池化也可以起到去噪作用；可以看作一种特殊的卷积操作。常见的池化操作有：最大池化、平均池化。

全连接层。以分类任务为例，将上述汇聚后的结果展平 (flatten) 为一个向量，再进行 softmax 即可。

现代卷积网络详见 计算机视觉，这里不再展开。

CNN 学习准则

同样是反向传播算法通过梯度下降进行优化。

CNN 优化算法

TODO

循环神经网络

监督学习任务：

  1. 序列到类别模式。例如「序列分类」中的情感分类任务：给定一个语言序列，分析序列的类别；
  2. 同步的序列到序列。例如「序列标注」任务中的中文分词：给定一个中文序列，对序列中每一个词语进行词性分析；
  3. 异步的序列到序列。例如「序列编码解码」任务中的机器翻译：输入序列和输出序列不需要有长度的严格对应关系。

时序预测任务：时序序列的数据集形如 \(\{ t_i,\boldsymbol{x}_i, y_i \}\)

  • 传统机器学习方法：自回归模型。具体的，模型 \(y_i=\beta_0 + \beta_1 y_{i-1} + \beta_2 y_{i-2} + \cdots + \beta_p y_{i-p}\) 被称为 P 阶自回归模型。可以看出这种模型仅仅利用到了标签值并且定义当前标签值与曾经的标签值呈线性关系；
  • 前沿深度学习方法：RNN 模型、LSTM 模型、时序卷积模型、Transformer。

网络优化

为了能够让一个网络模型「训练速度更快」和「泛化性能更好」，我们可以采用各种网络优化策略。针对一个神经网络，可以有如下五个角度的网路优化策略。

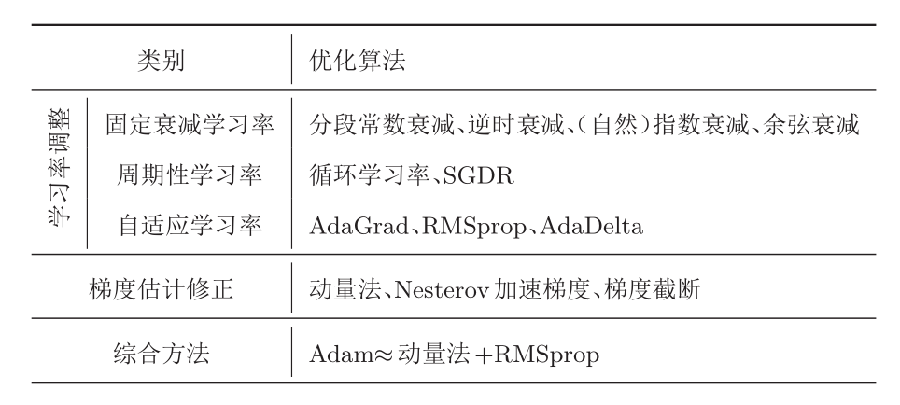
更好的优化算法：

更好的优化算法

更好的参数初始化方法：基于「范数保持性」的参数初始化方法。

更好的数据预处理方法：逐层归一化。

更好的网络结构：ReLU 激活函数、残差连接。

更好的超参数优化方法：

超参数：

  • 层数
  • 每层神经元个数
  • 激活函数
  • 学习率（以及动态调整算法）
  • 正则化系数
  • mini-batch 大小

超参数优化方法：

  • 网格搜索
  • 随机搜索
  • 贝叶斯优化
  • 动态资源分配
  • 神经架构搜索

mini-batch 与学习率的关系。对于网络中的超参数，如何进行选择呢？最朴素的方法就是网格搜索。对于随机梯度下降的参数优化算法，批大小与学习率一般成正比，即一批训练数据量越多，学习率越高。这是因为一批的训练数据越多，泛化能力就越高，对应的学习率就没必要太低。

学习率的动态调整算法。一般来说就是两个阶段，在初期的阶段，学习率线性增长，在之后的阶段中，学习率逐渐衰减。详情见 Facebook 的这篇论文 Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour [2018]。

下图展示了预热学习率调整的学习效果。图源：Bag of Tricks for Image Classification with Convolutional Neural Networks [2018]。

Visualization of learning rate schedules with warm-up. Top: cosine and step schedules for batch size 1024. Bottom: Top-1 validation accuracy curve with regard to the two schedules.

  1. 邱锡鹏.《神经网络与深度学习》[M]. 1版. 北京: 机械工业出版社, 2017. ISBN 978-7-111-64968-7. ↩