评价

模型训练好之后，需要判断其性能，根据不同的任务就有不同的评价指标。本文重点介绍模型评价中的自动评价指标，人为评价指标此处不展开。

回归任务

对于回归任务，模型输出的是一个具体的实数。

均方误差

均方误差 (Mean Square Error, MSE) 即模型预测值 \(f(\boldsymbol{x}_i)\) 与标签值 \(y_i\) 的平均平方误差，也就是所谓的方差。取值范围为 \([0,+\infty]\)，越小越好。如下式：

\[ \text{MSE} =\frac{1}{N} \sum_{i = 1}^N (f(\boldsymbol{x}_i) - y_i)^2 \]

\(R^2\) 分数

\(R^2\) 分数的取值范围为 \([-\infty,1]\)，越大越好。如下式：

\[ R^2 = 1 - \frac{\sum_{i = 1}^N(f(\boldsymbol{x}_i)-y_i)^2}{\sum_{i = 1}^N(\bar{y} - y_i)^2},\quad \bar{y} = \frac{1}{N}\sum_{i = 1}^N y_i \]

二分类任务

对于二分类任务，模型输出的大多都是样本属于正例的概率。

混淆矩阵

混淆矩阵 (confusion matrix) 即二分类模型的预测结果。

表 1. 二分类结果混淆矩阵

真实情况 \ 预测结果	正例	反例
正例	TP（真正例）	FN（假反例）
反例	FP（假反例）	TN（真反例）

基于上述混淆矩阵，我们定义以下度量指标：

表 2. 二分类度量指标（数据平衡时）

名称	公式	备注
准确率 (Accuracy)	\(\text{Accuracy}=\dfrac{TP+TN}{TP+FN+FP+TN}\)	错误率 = 1 - 准确率
查准率/精度 (Precision)	\(P = \dfrac{TP}{TP+FP}\)	该指标可以理解为「我认为的正例里面确实为正例的样本数量越多越好」。适用于商品搜索推荐，即在有限的屏幕内容中显示出尽可能多的用户偏好商品。
查全率/召回率 (Recall)	\(R = \dfrac{TP}{TP+FN}\)	该指标可以理解为「在测试集的所有正例里面预测为正例的样本数量越多越好」。适用于逃犯、病例检测，需要尽可能将正例检测出来。

当训练集正负例「不平衡」时，需要按照正负例分开评估。如下：

表 3. 二分类度量指标（数据不平衡时）

名称	公式	备注
敏感性 (Sensitivity)	\(\text{Sensitivity} = \dfrac{TP}{TP + FN}\)	该指标只评估模型对正例的预测准确性。
特异性 (Specificity)	\(\text{Specificity} = \dfrac{TN}{FP + TN}\)	该指标只评估模型对负例的预测准确性。

由于实际场景中需要「兼顾查准率和查全率」同时可能需要对其中一个有所偏好，我们引入 \(F_{\beta}\) 分数。当 \(\beta=1\) 时就是标准的 F1 分数，当 \(\beta>1\) 时对查全率有偏好，当 \(\beta<1\) 时对查准率有偏好。\(F_{\beta}\) 分数如下式：

\[ F_{\beta} = \frac{(1+\beta^2) \cdot P \cdot R}{\beta^2\cdot P + R} \]

Tip

上述指标都是针对一个混淆矩阵展开，如果需要度量「二分类模型的泛化能力」是远远不够的。为此我们引入 P-R 曲线和 ROC 曲线。两者的产生方式相同，都是：根据二分类模型对测试数据类别的预测概率划分一个阈值，并将预测概率超过阈值的判定为正例，低于阈值的判定为负例。然后将阈值依次选择为每个样本（假设为 \(N\) 个测试样本）的预测概率值进行二分类即可得到 \(N\) 个混淆矩阵，进而得到曲线中的 \(N\) 个数据点。

P-R 曲线

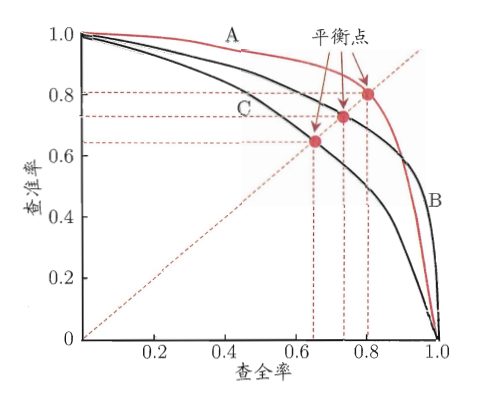
横坐标为查全率 (Recall)，纵坐标为查准率 (Precision)。

趋势解读。随着正例判定阈值不断下降，很显然查全率 \(R\) 会不断上升，查准率 \(P\) 会不断下降；
曲线解读。不同曲线对应了不同模型的泛化能力，我们用「P-R 曲线与横纵坐标围成的面积」来衡量模型的泛化能力，面积越大则对应模型的泛化性能更好。因此上图中 A 模型泛化能力比 C 模型要好。但是我们往往会遇到比较 \(A\) 与 \(B\) 两个模型泛化能力的情况，考虑到计算实际曲线面积的复杂性，引入「平衡点」概念。平衡点就是 \(P=R\) 这条直线与 P-R 曲线的交点。平衡点越高，则对应的模型泛化能力越好。因此上图中 \(A\) 模型的性能优于 \(B\) 模型的性能。

ROC 曲线

ROC (Receiver Operating Characteristic, ROC) 曲线即受试者工作特征曲线。横坐标为假正例率 \(\displaystyle FPR = \frac{FP}{FP+TN}\)，纵坐标为真正例率 \(\displaystyle TPR = \frac{TP}{TP+FN}\)。

趋势解读。随着正例判定阈值不断下降，真正例率与假正例率均会不断上升；
曲线解读。不同曲线同样对应了不同模型的泛化能力。我们用「ROC 曲线下方的面积 (Area Under ROC Curve, AUC)」来衡量模型的泛化能力，面积越大则对应模型的泛化性能越好。取值范围为 \([0.5,1]\)，其中 \(0.5\) 表示模型进行随机预测的性能。

多分类任务

我们可以将多分类问题拆分为多个二分类问题（假设为 \(n\) 个），从而可以获得多个混淆矩阵。根据求平均顺序的不同，多分类任务的度量指标分为「宏」与「微」两个类别。其中宏是先求指标再取平均，微是先取平均再求指标。

表 4. 多分类任务度量指标表

类别 \ 指标	查准率	查全率	F1 分数
宏	\(\displaystyle\text{macroP} = \frac{1}{n} \sum_{i=1}^n P_i\)	\(\displaystyle \text{macroR} = \frac{1}{n} \sum_{i=1}^n R_i\)	\(\displaystyle\text{macroF}_1 = \frac{2 \cdot\text{macroP} \cdot\text{macroR}}{\text{macroP}+\text{macroR}}\)
微	\(\displaystyle\text{microP} = \frac{\overline{TP}}{\overline{TP}+\overline{FP}}\)	\(\displaystyle\text{microR} = \frac{\overline{TP}}{\overline{TP}+\overline{FN}}\)	\(\displaystyle\text{microF}_1 = \frac{2 \cdot \text{microP} \cdot \text {microR}}{\text{microP}+\text{microR}}\)