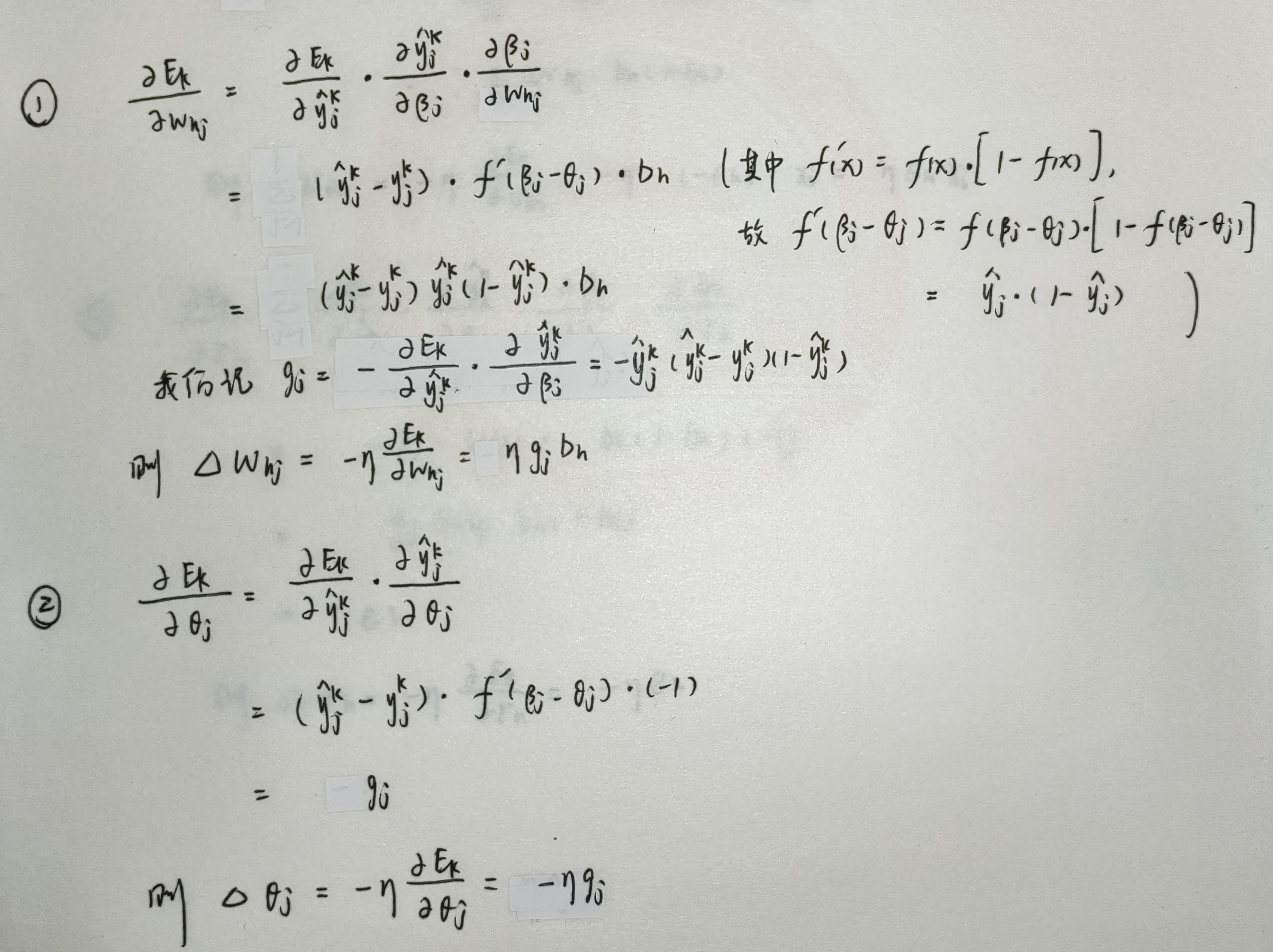跳转至

深度学习导读

前言

本文记录深度学习入门笔记。教材主要参考邱锡鹏老师的《神经网络与深度学习》1 2 3，其余参考内容：

绪论

表示学习是什么？与传统的特征工程目的一致，为了得到数据中的更好的特征。不同的是，特征工程中的特征选择、特征映射等策略都是手动可控的方式，而表示学习就是利用深度神经网络从数据中自动学习高层的有效特征。

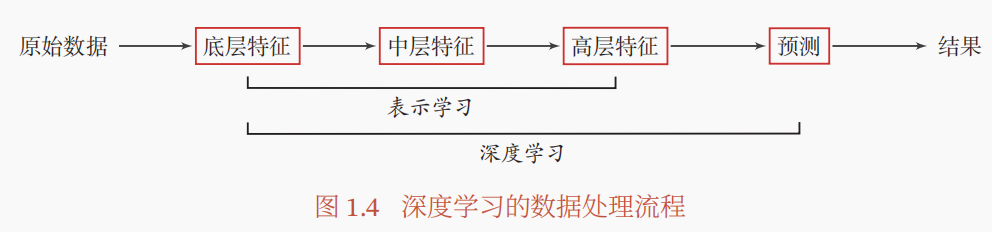
深度学习是什么？我们知道机器学习就是在「手动处理完特征」后，构建对应的模型「预测输出」。而深度学习就是将机器学习的手动特征工程也用模型进行「表示学习」来学习出有效特征，然后继续构建模型「预测输出」。如下图所示：

深度学习的数据处理流程

为什么会有深度学习？最简单的一点就是，很多特征我们根本没法定义一种表示规则来表示特征，比如说对于图像，怎么定义复杂的图像的特征呢？比如说对于音频，又怎么定义复杂的音频的特征呢？没办法，我们直接学特征！

神经网络是什么？就是万千模型中的一种，仅此而已。

为什么用神经网络进行深度学习？有了上面对深度学习定义的理解，可以发现其中最具有挑战性的特点就是，模型怎么知道什么才是好特征？什么是不好的特征？神经网络可以很好的解决这个问题。通过由浅到深层层神经元的特征提取，深层的神经元就可以学习更高语义的特征，并且通过这种方式也可以实现「端到端」的学习方式，而不用像机器学习的方法那样，先选特征再学习。并且神经网络模型也可以很好的解决深度学习中特征的「贡献度分配」问题。

人工神经元

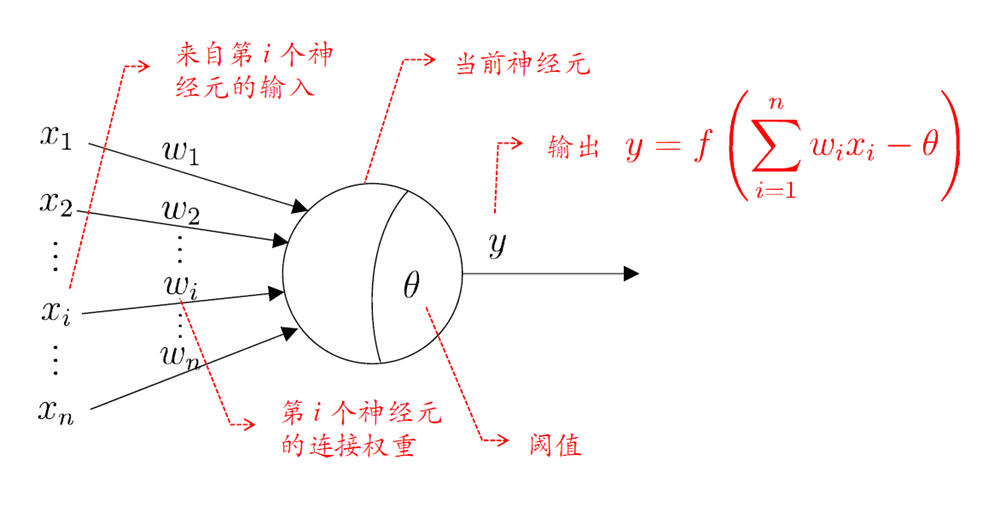
人工神经元模型

图 1. 人工神经元模型

神经元是网络模型中的最小学习单元。每一个神经元接受输入 \(\sum_{i=1}^n w_ix_i - \theta\)，通过设定好的激活函数 \(f\) 得到该神经元对应的输出值 \(f(\sum_{i=1}^n w_ix_i - \theta)\)。其中 \(\theta\) 可以理解为神经元的激活阈值，也可以理解为神经元模型中的偏置项。

神经元中的激活函数大有门道、种类极多。为了确保网络可以拟合复杂的映射关系，需要激活函数是「非线性」的；为了便于对网络求导从而进行参数更新，需要确保激活函数是「可导」的；为了防止对网络求导的过程中出现梯度消失或者梯度爆炸，需要确保激活函数是「单调并且有界」。主要有以下 3 种类型：

  • S 型函数。例如 Sigmoid 函数、Tanh 函数；
  • 斜坡函数。例如 ReLU 函数；
  • Swish 函数。复合函数。

全连接神经网络

全连接神经网络 (Full Connect Neural Network) 又称前馈神经网络 (Feedforward Neural Network)、感知机 (Perceptron)，是深度神经网络模型的开山鼻祖，通过向前传递数据，向后更新参数，实现学习和拟合的功能。

全连接神经网络模型的学习准则一般采用交叉熵损失，优化算法一般采用小批量随机梯度下降 (Mini-batch Stochastic Gradient Descent, 简称 Mini-batch SGD) 算法。

模型

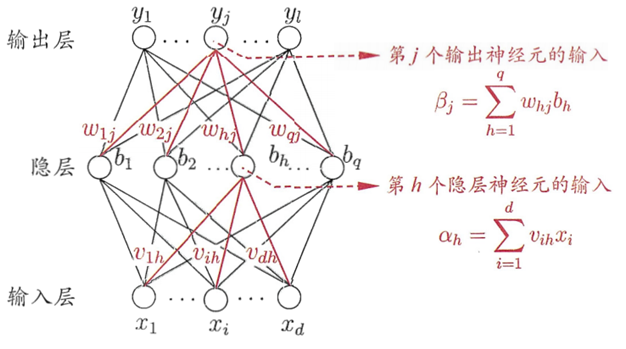
两层全连接神经网络

图 2. 两层全连接神经网络模型

Tip

在神经网络模型中，我们定义输入层为前，输出层为后。

功能简介。所谓全连接神经网络，就是各层神经元之间不会跨层连接，也不存在同层连接，其中：

  • 输入层仅仅接受外界输入，没有函数处理功能；
  • 隐藏层和输出层进行函数处理。

神经元的输入与输出。分为「有函数处理功能」和「无函数处理功能」两类：

  • 隐藏层：对于隐藏层的第 \(h\) 个神经元
    • 输入：\(\alpha_h = \sum_{i=1}^dx_i v_{ih}\)
    • 输出：\(b_h = f(\alpha_h - \gamma_h)\)
  • 输出层：对于输出层的第 \(j\) 个神经元
    • 输入：\(\beta_j=\sum_{h=1}^q b_h w_{hj}\)
    • 输出：\(\hat y_j = f(\beta j - \theta_j)\)

网络参数。现在给定一个训练集学习一个分类器。其中每一个样本都含有 \(d\) 个特征，\(l\) 个输出。每输入一个样本都迭代一次。对于单隐层神经网络而言，一共有 4 种参数，即：

  • 输入层到隐层的 \(d \times q\) 个权值 \(v_{ih}(i=1,2,\cdots,d,\ h=1,2,\cdots,q)\)
  • 隐层的 \(q\) 个神经元的阈值 \(\gamma_h(h=1,2,\cdots,q)\)
  • 隐层到输出层的 \(q\times l\) 个权值 \(w_{hj}(h=1,2,\cdots,q,\ j=1,2,\cdots,l)\)
  • 输出层的 \(l\) 个神经元的阈值 \(\theta_j(j=1,2,\cdots,l)\)

学习准则

假设每次输入一个训练样本进行参数更新（即 batch size = 1）。由于网络输出内容是实数，因此我们定义目标函数 \(\mathcal L\) 为当前训练样本的「均方误差」。那么对于第 \(k\) 个训练样本，就有如下损失：

\[ \mathcal L_k = \frac{1}{2} \sum _{j = 1}^l (\hat y_j^k - y_j^k)^2 \]

其中：为了求导方便，添加一个常量 \(\dfrac{1}{2}\)。\(\hat y\) 为样本真实值，\(y\) 为样本预测值。

优化算法

在进行梯度下降时，经过简单的推导可以发现，第 \(l\) 层的损失 \(\delta (l)\) 依赖于后一项的损失 \(\delta(l+1)\)，于是参数更新的逻辑就是从输出层开始逐层往后更新，直到第一层隐藏层。为此，我们引入著名的优化算法：误差逆传播算法 (error Back Propagation, BP)，其算法流程如下图所示：

误差逆传播算法流程

图 3. 误差逆传播算法流程

以上述单隐层神经网络为例，尝试推导参数更新的过程。假定学习率（搜索步长）为 \(\eta\)，那么上述 4 种参数的迭代公式就为：

\[ \begin{aligned} w_{hj} &\leftarrow w_{hj}+\Delta w_{hj} \\ \theta_{j} &\leftarrow \theta_{j}+\Delta \theta_{j} \\ v_{ih} &\leftarrow v_{ih}+\Delta v_{ih} \\ \gamma_{h} &\leftarrow \gamma_{h}+\Delta \gamma_{h} \\ \end{aligned} \]

其中，修正量分别为：

\[ \begin{aligned} \Delta w_{hj} &= \eta g_j b_h \\ \Delta \theta_{j} &= -\eta g_j \\ \Delta v_{ih} &= \eta e_h x_i \\ \Delta \gamma_{h} &= -\eta e_h \\ \end{aligned} \]
修正量推导 - 链式法则

公式表示：

公式表示

隐层到输出层的权重、输出神经元的阈值：

隐层到输出层的权重、输出神经元的阈值

输入层到隐层的权重、隐层神经元的阈值：

输入层到隐层的权重、隐层神经元的阈值

卷积神经网络

为了解决全连接网络不能学习到局部不变性的缺点，卷积网络应运而生。卷积网络有三大特征：局部连接、权重共享、时/间上的次采样。

卷积方式

等宽卷积、宽卷积、窄卷积；

转置卷积；

空洞卷积。

卷积网络

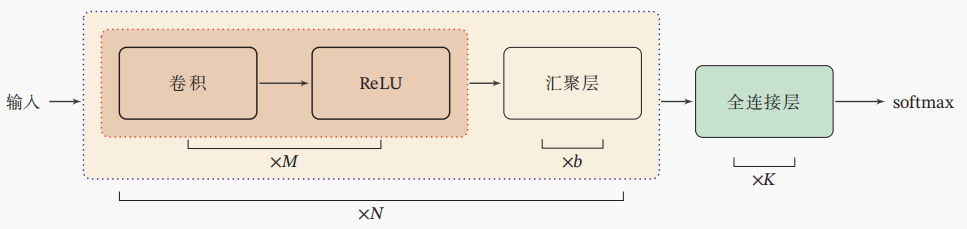
卷积神经网络的典型结构如下图所示：

卷积神经网络的典型结构

图 4. 卷积神经网络的典型结构

卷积层。对于二维卷积而言，我们假设输入共有 D 个图像，需要学习 P 个特征，并不是只需要学习 P 个卷积核的，对于每一个特征需要单独对每一张图像学习一个卷积核，因此需要学习 \(D\times P\) 个卷积核。

汇聚层 / 池化层。从上面的卷积层学习逻辑可以看出其实参数量和全连接层相比还是很大。池化层就是通过压缩卷积核大小来降低参数量；与此同时，通过池化也可以起到去噪作用。

其他卷积网络：

  • AlexNet [2012]。使用了 ReLU 激活函数，使用 GPU 并行计算，使用了数据增强；
  • VGGNet。
  • Inception 网络 [v3, 2016]。将多个等宽卷积的结果进行堆叠；
  • 残差网络。由于恒等模型 \(f(x)=x\) 无法学习到，故将线性模型转化为 \(f(x) = x + [f(x) - x]\) 并来学习新的模型 \(f(x)-x\)。可以解决梯度消失的问题；
  • GoogleNet。
  • DenseNet。

参数学习

同样是反向传播算法通过梯度下降进行优化。

循环神经网络

监督学习任务：

  1. 序列到类别模式。例如「序列分类」中的情感分类任务：给定一个语言序列，分析序列的类别；
  2. 同步的序列到序列。例如「序列标注」任务中的中文分词：给定一个中文序列，对序列中每一个词语进行词性分析；
  3. 异步的序列到序列。例如「序列编码解码」任务中的机器翻译：输入序列和输出序列不需要有长度的严格对应关系。

时序预测任务：时序序列的数据集形如 \(\{ t_i,\boldsymbol{x}_i, y_i \}\)

  • 传统机器学习方法：自回归模型。具体的，模型 \(y_i=\beta_0 + \beta_1 y_{i-1} + \beta_2 y_{i-2} + \cdots + \beta_p y_{i-p}\) 被称为 P 阶自回归模型。可以看出这种模型仅仅利用到了标签值并且定义当前标签值与曾经的标签值呈线性关系；
  • 前沿深度学习方法：RNN 模型、LSTM 模型、时序卷积模型、Transformer。

网络优化

为了能够让一个网络模型「训练速度更快」和「泛化性能更好」，我们可以采用各种网络优化策略。针对一个神经网络，可以有如下五个角度的网路优化策略。

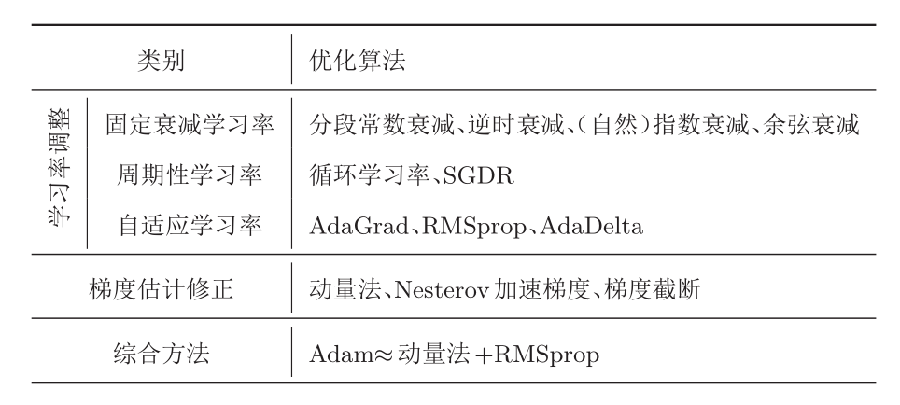
更好的优化算法：

更好的优化算法

更好的参数初始化方法：基于「范数保持性」的参数初始化方法。

更好的数据预处理方法：逐层归一化。

更好的网络结构：ReLU 激活函数、残差连接。

更好的超参数优化方法：

超参数：

  • 层数
  • 每层神经元个数
  • 激活函数
  • 学习率（以及动态调整算法）
  • 正则化系数
  • mini-batch 大小

超参数优化方法：

  • 网格搜索
  • 随机搜索
  • 贝叶斯优化
  • 动态资源分配
  • 神经架构搜索

mini-batch 与学习率的关系。对于网络中的超参数，如何进行选择呢？最朴素的方法就是网格搜索。对于随机梯度下降的参数优化算法，批大小与学习率一般成正比，即一批训练数据量越多，学习率越高。这是因为一批的训练数据越多，泛化能力就越高，对应的学习率就没必要太低。

学习率的动态调整算法。一般来说就是两个阶段，在初期的阶段，学习率线性增长，在之后的阶段中，学习率逐渐衰减。详情见 Facebook 的这篇论文 Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour [2018]。

下图展示了预热学习率调整的学习效果。图源：Bag of Tricks for Image Classification with Convolutional Neural Networks [2018]。

Visualization of learning rate schedules with warm-up. Top: cosine and step schedules for batch size 1024. Bottom: Top-1 validation accuracy curve with regard to the two schedules.

  1. 邱锡鹏.《神经网络与深度学习》[M]. 1版. 北京: 机械工业出版社, 2017. ISBN 978-7-111-64968-7. ↩

  2. https://nndl.github.io/ ↩

  3. https://github.com/nndl/ ↩