贝叶斯模型

极大似然估计

根本任务：寻找合适的参数 $\hat \theta$ 使得「当前的样本情况发生的概率」最大。又由于假设每一个样本相互独立，因此可以用连乘的形式表示上述概率，当然由于概率较小导致连乘容易出现浮点数精度损失，因此尝尝采用取对数的方式来避免「下溢」问题。也就是所谓的「对数似然估计」方法。

我们定义对数似然 $\text{(log-likelihood)}$ 估计函数如下：

$$\begin{aligned} LL(\theta_c) &= \log P(D_c\ |\ \theta_c) \\ &= \sum_{x \in D_c} \log P(x\ |\ \theta_c) \end{aligned}$$

此时参数 $\hat \theta$ 的极大似然估计就是：

$$\hat \theta_c = \arg \max_{\theta_c} LL(\theta_c)$$

朴素贝叶斯分类器

我们定义当前类别为 $c$，则 $P(c)$ 称为类先验概率，$P(x\ |\ c)$ 称为类条件概率。最终的贝叶斯判定准则为：

$$P(c\ |\ x) = \frac{P(c)P(x\ |\ c)}{P(x)}$$

现在假设 各属性之间相互独立，则对于拥有 d 个属性的训练集，在利用贝叶斯定理时，可以通过连乘的形式计算类条件概率 $P(x \ | \ c)$，于是上式变为：

$$P(c\ |\ x) = \frac{P(c)}{P(x)} \prod_{i = 1}^d P(x_i\ |\ c)$$

注意点：

• 对于离散数据。上述类条件概率的计算方法很好计算，直接统计即可
• 对于连续数据。我们就没法直接统计数据数量了，替换方法是使用高斯函数。我们根据已有数据计算得到一个对于当前属性的高斯函数，后续计算测试样例对应属性的条件概率，代入求得的高斯函数即可。
• 对于类条件概率为 0 的情况。我们采用拉普拉斯修正。即让所有属性的样本个数 $+1$，于是总样本数就需要 $+d$ 来确保总概率仍然为 $1$。这是额外引入的 bias

半朴素贝叶斯分类器

朴素贝叶斯的问题是假设过于强，现实不可能所有的属性都相互独立。半朴素贝叶斯弱化了朴素贝叶斯的假设。现在假设每一个属性最多只依赖一个其他属性。即独依赖估计 (One-Dependent Estimator, ODE)，于是就有了下面的贝叶斯判定准测：

$$P(c\ |\ x) \propto P(c) \prod _{i = 1}^d P(x_i\ |\ c, pa_i)$$

如何寻找依赖关系？我们从属性依赖图出发

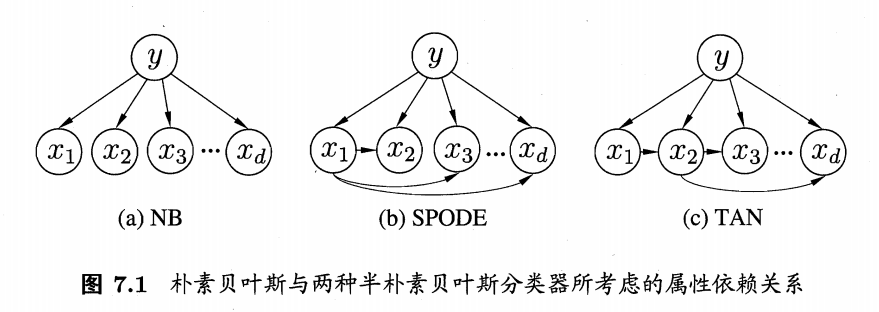
如上图所示：

• 朴素贝叶斯算法中：假设所有属性相互独立，因此各属性之间没有连边
• SPODE 确定属性父属性算法中：假设所有属性都只依赖于一个属性（超父），我们只需要找到超父即可
• TAN 确定属性父属性算法中：我们需要计算每一个属性之间的互信息，最后得到一个以互信息为边权的完全图。最终选择最大的一些边构成一个最大带权生成树
• AODE 确定属性父属性算法中：采用集成的思想，以每一个属性作为超父属性，最后选择最优即可

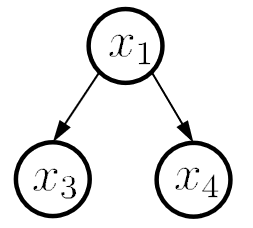
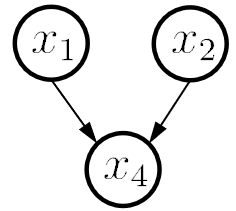
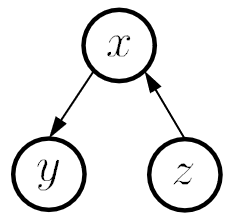
贝叶斯网

构造一个关于属性之间的 DAG 图，从而进行后续类条件概率的计算。三种典型依赖关系：

同父结构	V 型结构	顺序结构
在已知 $x_1$ 的情况下 $x_3,x_4$ 独立	若 $x_4$ 未知则 $x_1,x_2$ 独立，反之不独立	在已知 $x$ 的情况下 $y,z$ 独立

概率计算公式参考：超详细讲解贝叶斯网络(Bayesian network)

EM 算法

现在我们需要解决含有隐变量 $Z$ 的情况。如何在已知数据集含有隐变量的情况下计算出模型的所有参数？我们引入 EM 算法。EM 迭代型算法共两步

• E-step：首先利用观测数据 $X$ 和参数 $\Theta_t$ 得到关于隐变量的期望 $Z^t$
• M-step：接着对 $X$ 和 $Z^t$ 使用极大似然函数来估计新的最优参数 $\Theta_{t+1}$

有两个问题：哪来的参数？什么时候迭代终止？

• 对于第一个问题：我们随机化初始得到参数 $\Theta_0$
• 对于第二个问题：相邻两次迭代结果中 参数 差值的范数小于阈值 $(|| \theta^{(i+1)} - \theta^{(i)}) || < \epsilon_1)$ 或 隐变量条件分布期望 差值的范数小于阈值 $(|| Q(\theta^{(i+1)} , \theta^{(i)})) - Q(\theta^{(i)} , \theta^{(i)}) || < \epsilon_2)$