决策树模型

下面介绍一个经典的机器学习模型：决策树模型。可以利用该模型完成监督学习任务，比如常见的分类与回归。下面将会花较多篇幅讲解决策树模型在分类任务上的应用。

当然，决策树模型绝不至于此，基于这种划分决策的思想诞生出了很多别的模型，例如：异常检测任务中的孤立森林模型、集成学习任务中的基学习器模型等等，留给读者进一步探索。

基本概念

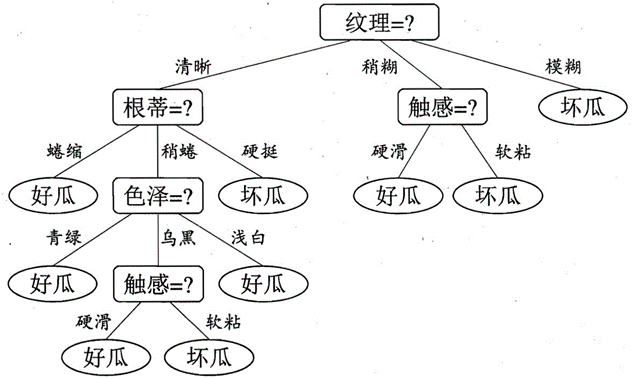
决策树的结构如上图所示。决策树算法遵循自顶向下、分而治之的思想。叶子结点表示分类结果、边表示属性划分、分支结点表示属性选择。

决策树的算法伪代码如上图所示。下面依次解释：

生成分支结点：选择最优的属性作为当前结点决策依据；
生成所有的边：根据当前分支结点的属性在 测试数据 中所有可能的属性取值生成所有的分支；
生成孩子结点：将当前结点的样本根据每一条边对应的属性取值依次划分到对应的孩子结点中；
不断递归：不断重复上述 1-3 步直到递归终点，有以下三种递归终点：
- 当前结点的训练样本类别均属于某个类别。则将当前结点设定为叶子结点，并标记当前叶子结点对应的类别为 当前结点同属的类别；
- 当前结点的训练样本数为 \(0\)。则将当前结点为设定为叶子结点，并标记当前叶子结点对应的类别为 父结点中最多类别数量对应的类别；
- 当前结点的训练样本的所有属性值都相同。则将当前结点设定为叶子结点，并标记当前叶子结点对应的类别为 当前训练样本中最多类别数量对应的类别。

划分策略

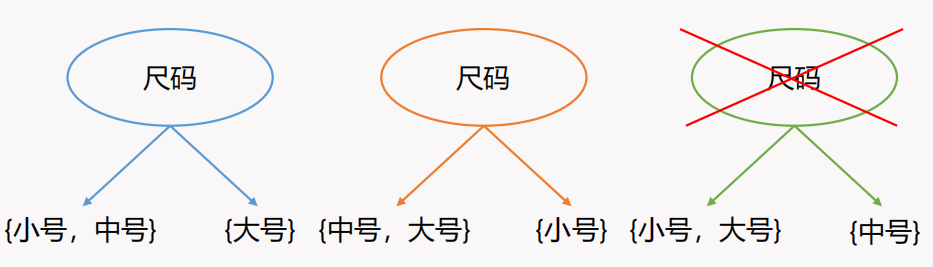
一般而言，决策树中每一个结点的分支数量可以是两个，即二路划分，也可以是多个，即多路划分。显然就需要对连续的数值属性进行离散化。但无论是类别属性（二元属性、标称属性、序数属性）还是离散化后的数值属性，划分时都要遵守分组的合法性，如下图所示：

属性选择

在递归建树时，如何选择出当前局面下的最优属性来划分样本呢？我们「希望当前结点的所包含的样本尽可能属于同一类」这一根本目的出发，讨论三种最优属性选择策略。

信息增益

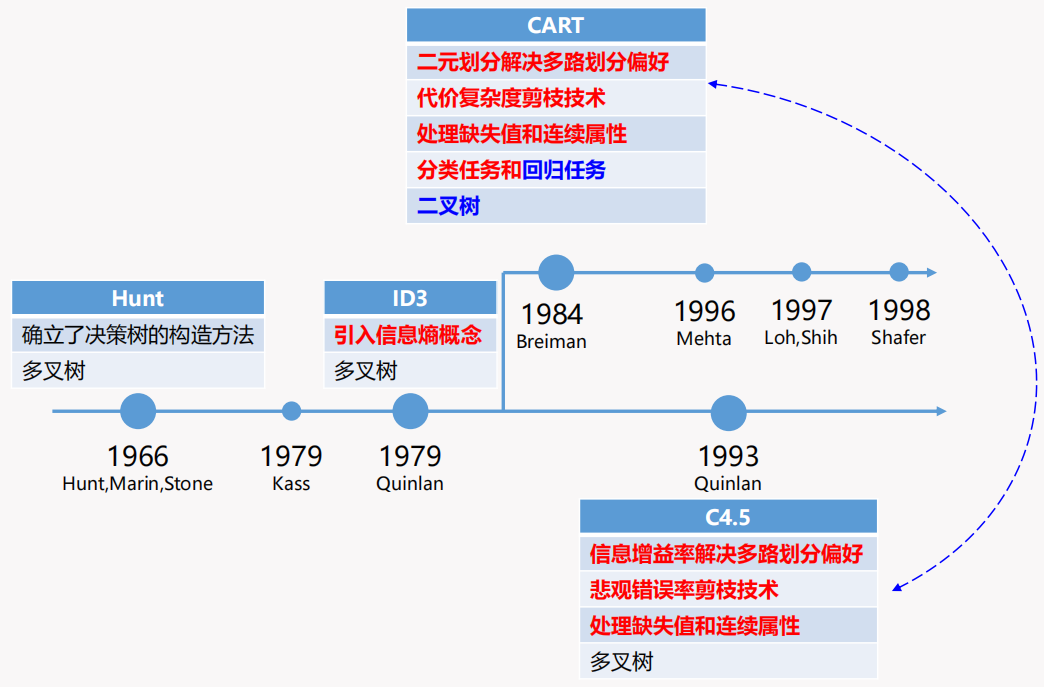
Iterative dichotomiser 3 (ID3) 算法首次在机器学习中引入了信息的概念。具体的：

信息量 (Amount of information)。对于一个随机事件 \(X\)，其发生的概率为 \(P\)，则该事件是否发生对应的信息量为 \(-\log_2 P\)。可以看出，一个随机事件发生的可能性越大，对应的信息量就越少；
信息熵 (Information Entropy)。信息熵就是所有随机事件 \(X_i, i \in N\) 信息量的期望。假设第 \(i\) 个随机事件 \(X_i\) 发生的概率为 \(P_i\)，则这些事件的信息熵为 \(-\sum_{i=1}^N P_i \log_2P_i\)。

而 ID3 算法选择最优属性的核心思路就是选择划分后使得信息增益 (Information gain) 最大的属性。

我们记训练集为 \(D\)，可供选择的属性列表为 \(a,b,\cdots,\gamma\)，随机事件定义为当前训练集中每一个类别的占比。假设当前样本集合中含有 \(t\) 个类别，第 \(k\) 个类别所占样本集合比例为 \(P_k\)，则当前训练集的信息熵 \(\text{Ent}(D)\) 为：

\[ \text{Ent}(D) = -\sum _{k = 1}^t P_k \log_2(P_k) \]

属性 \(a\) 共有 \(V\) 个属性取值，即 \(a=\{a^1,a^2,\cdots.a^V\}\)，于是便可以将当前结点对应的训练数据集 \(D\) 划分为 \(V\) 个子结点的训练数据 \(D=\{D^1,D^2,\cdots.D^V\}\)，由于每一个子结点划到的训练数据量不同，引入权重，则以 a 作为划分属性时得到的信息增益为：

\[ \text{Ent\_Gain}(D, a)=\text{Ent}(D) - \sum_{i = 1}^V \frac{|D^i|}{|D|} \text{Ent}(D^i) \]

信息增益率

由于 ID3 算法使用信息增益选择最优属性进行划分时，会在属性的取值较多时有偏好，C4.5 算法对其进行了改进。同时 C4.5 算法考虑了连续的数值属性离散化、缺失值处理和剪枝技术，这都会在接下来的小节中具体展开。

不过所谓的属性选择策略的优化，其实就是在 ID3 的基础上增加了一个规范化，信息增益率的定义式如下：

\[ \text{Ent\_Gain}\_\text{ratio}(D, a) = \frac{\text{Ent\_Gain}(D, a)}{\text{IV}(D, a)} \]

其中 \(\text{IV}(D, a)\) 为：

\[ \text{IV}(D, a) = -\sum_{i = 1}^V \frac{|D^i|}{|D|} \log_2 \frac{|D^i|}{|D|} \]

可以看出 \(\text{IV}(D, a)\) 其实就是数据集 \(D\) 在属性 \(a\) 所以可能取值上的信息熵。一般而言，属性的属性取值越多，信息增益越大，对应的 \(\text{IV}\) 值也越大，这样就可以规范化信息增益，避免在选择最优划分属性时模型偏好于更多属性取值的属性了。

基尼指数增益

分类与回归树 (Classification And Regression Tree, CART) 算法在决策树模型中引入了基尼指数 (Gini index) 来进行最优划分属性的选择。基尼指数是用来衡量一个国家或地区的收益差距的指标，基尼指数越小则表明收入差距越小。

假设当前结点对应的样本集合为 D，其中含有 \(t\) 个类别并且第 \(k\) 个类别所占样本集合比例为 \(P_k\)，则当前结点的基尼指数为：

\[ \text{Gini(D)} = 1 - \sum_{k = 1}^{t}P_k^2 \]

于是选择属性 \(a\) 作为划分属性的的基尼指数增益 \(\text{Gini\_Gain}(D,a)\) 为：

\[ \text{Gini\_Gain}(D,a) = \text{Gini(D)} - \sum_{i = 1}^V \frac{|D^i|}{|D|} \text{Gini}(D^i) \]

剪枝处理

为了防止模型过拟合并且降低计算复杂度，我们需要使用验证集对决策树进行剪枝。一共有两种剪枝方法：

预剪枝。基于贪心的思想，决策每次划分是否需要进行。我们知道最佳属性的选择是基于信息增益等关于结点纯度的算法策略，而是否进行子结点的生成需要我们进行性能评估，即从测试精度的角度来考虑。因此决策划分是否进行取决于子结点生成前后在验证集上的测试精度，如果可以得到提升则进行生成，反之则不生成子结点，也就是预剪枝的逻辑；
后剪枝。同样是预剪枝的精度决策标准。我们在一个决策树完整生成以后，从深度最大的分支结点开始讨论是否可以作为叶子结点，也就是是否删除该分支的子结点。决策的依据是删除子结点前后在测试集上的精度是否有提升，如果有则删除子结点，反之不变。

两种剪枝策略的区别在于。预剪枝是基于贪心，也就是说没有考虑到全局的情况，可能出现当前结点划分后测试精度下降，但是后续结点继续划分会得到性能提升，从而导致预剪枝的决策树泛化性能下降；而后剪枝就可以规避贪心导致的局部最优，但是计算的时间开销更大。

连续与缺失值

连续值处理

这里讲解二分法 (bi-partition)。主要就是在计算信息增益时增加了一步，将属性的取值情况划分为了两类。那么如何划分呢？关键在于划分点的取值。假设当前属性 a 的取值是连续值，去重排序后得到 n 个数值，我们取这 n 个数值的 n-1 个间隔的中值作为划分点集合，枚举其中的每一个划分点计算最大信息增益，对应的划分点就是当前连续取值的属性的二分划分点。~~时间复杂度极高！也不知道 C4.5 算法怎么想的~~

缺失值处理

当然我们可以直接删除含有缺失信息的样本，但是这对数据信息过于浪费，尤其是当数据量不大时，如何解决这个问题呢？我们需要解决两个问题：

在选择最优划分属性时，如何计算含有缺失值的属性对应的信息增益呢？
在得到最优划分属性时，如何将属性值缺失的样本划分到合理的叶子结点呢？

对于第一个问题：只计算属性值没有缺失的样本，然后放缩到原始的数据集合大小即可

对于第二个问题：对于已知属性值的样本，我们可以计算出每一个属性值的样本数量，从而计算出一个集合比例，这样对于未知属性值的样本，只需要按照前面计算出来的集合，按照概率划分到对应的子结点即可

多变量决策树

很好，本目就是来解决上述连续值处理的过高时间复杂度的问题的。现在对于一个结点，不是选择最优划分属性，而是对建一个合适的线性分类器，如图：