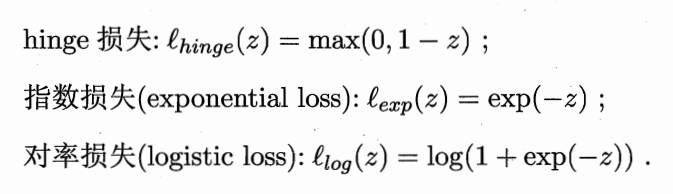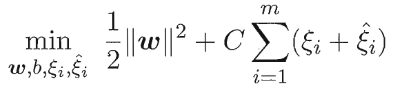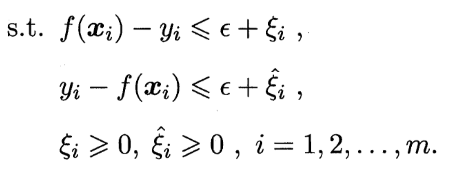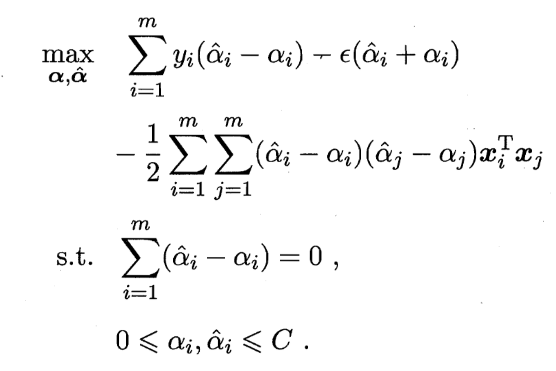线性模型

本章介绍机器学习模型中的线性模型。基本形式如下：

\[ \begin{aligned} &f(\boldsymbol {x}) = \boldsymbol {w}^T \boldsymbol {x} \\ &\boldsymbol {w} \in R^{D+1}, \boldsymbol {x} \in R^{D+1} \end{aligned} \]

其中 \(\boldsymbol {w} = [w_1,w_2,\cdots,w_D,b]^T, \boldsymbol {x} = [x_1,x_2,\cdots,x_D,1]^T\) 均为增广向量。样本的特征个数为 \(D\)，样本的总个数为 \(N\)，模型为 \(f(\cdot)\)。

基于此模型，我们就可以通过机器学习来进行分类与回归任务。值得注意的是，尽管线性模型无法解决线性不可分的问题，但其强就强在形式简单、易于建模以及高可解释性，同时也是很多非线性模型的基础。

线性回归

线性回归顾名思义就是利用线性模型解决「回归」任务。

模型

线性回归表达式就是最基本的线性模型表达式，因为最基本的线性模型最终的输出就是一个实数。

学习准则

我们定义学习准则为平方误差，那么损失函数 \(\mathcal L_{\boldsymbol w}\) 就是：

\[ \mathcal L_{\boldsymbol w} = (\boldsymbol y -\boldsymbol X \boldsymbol w) ^T (\boldsymbol y - \boldsymbol X\boldsymbol w) \]

其中 \(\boldsymbol X\) 是输入样本的增广矩阵 \(\boldsymbol{X}_{N\times (D+1)}\)：

\[ \boldsymbol{X}=\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1D} & 1 \\ x_{21} & x_{22} & \cdots & x_{2D} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{N1} & x_{N2} & \cdots & x_{ND} & 1 \end{bmatrix} \]

优化算法

为了最小化这个损失函数，我们用最常规的梯度下降算法。令 \(\dfrac{\partial \mathcal L_{\boldsymbol w}}{\partial \boldsymbol w}=0\)，得：

\[ \boldsymbol X^T\boldsymbol X \boldsymbol w = \boldsymbol X^T \boldsymbol y \]

情况一：若 \(\boldsymbol X^T \boldsymbol X\) 可逆，则最佳参数 \(\boldsymbol w^*\) 就是一个闭式解：

\[ \boldsymbol w^* = (\boldsymbol X^T \boldsymbol X)^{-1}\boldsymbol X^T \boldsymbol y \]

情况二：若 \(\boldsymbol X^T \boldsymbol X\) 不可逆，我们引入 \(L_2\) 正则化项 \(\alpha \| \boldsymbol w \|^2\)。现在的损失函数形为：

\[ \mathcal L_{\boldsymbol w} = (\boldsymbol y - \boldsymbol X \boldsymbol w) ^T (\boldsymbol y - \boldsymbol X \boldsymbol w) + \alpha \| \boldsymbol w \|^2 \]

上式有一个别名叫做「岭回归」。同样令 \(\dfrac{\partial \mathcal L_{\boldsymbol w}}{\partial \boldsymbol w}=0\)，得：

\[ \boldsymbol w^* = (\boldsymbol X^T \boldsymbol X + \alpha \boldsymbol I)^{-1} \boldsymbol X^T \boldsymbol y \]

上式中 \(\alpha\) 就变成了超参数。

逻辑回归

若想要利用线性回归的实数结果进行「二分类」，我们需要将回归结果映射成一个固定区间，便于定义阈值从而二分类。常见的映射函数如下：

\[ g(x) = \frac{1}{1+e^{-x}} \]

该函数被叫做：逻辑函数 (logistic function)。不过在深度学习里面这又被叫做 sigmoid 激活函数。该函数的数学性质比较好，比如她是任意阶连续可导的凸函数，以及她的值域是 \((0,1)\)。如下图所示：

模型

基于「逻辑函数」与「线性回归」的逻辑回归二分类模型定义为：

\[ y = \sigma(\boldsymbol{w}^T\boldsymbol{x}) = \frac{1}{1+e^{-\boldsymbol{w}^T\boldsymbol{x}}} \]

模型有一个可学习参数「权重向量 \(\boldsymbol {w}\)」和一个不可学习的超参数「二分类映射阈值 \(\text{threshold}\)」。其中：

权重向量 \(\boldsymbol{w}\) 已经包含了偏执项 \(b\)，因此参数个数为 \(D+1\)；
分类映射阈值 \(\text{threshold}\) 需要人为定义。

由于我们将正例标记为 \(1\)，将负例标记为 \(0\)，且逻辑函数可以将实数域单调递增地压缩到 \((0,1)\) 之间，因此我们可以将逻辑回归模型输出的结果视为「样本属于正例的后验概率」，即 \(p(y=1 \ | \ \boldsymbol x)\)。

至于为什么叫做「后验」，是因为逻辑回归模型已经知道了输入的 \(x\)，也就是已经知道了某一个前提了。反之如果不知道任何前提直接建模事件发生的概率，就叫做先验概率。

学习准则

我们采用最大似然估计 (Maximum Likelihood Estimation, MLE)，即在没有任何先验假设的情况下估计模型的参数使得当前的数据发生的概率最大。这是频率派的一种参数估计策略。

若我们将 \(y\) 视作类后验概率 \(p(y=1 \ | \ x)\)，则有

\[ \ln \frac{p(y = 1 \ | \ x)}{p(y = 0 \ | \ x)} = w^Tx+b \]

同时，显然有

\[ \begin{aligned} p(y = 1 \ | \ x) = \frac{1}{1 + e^{-(w^Tx+b)}} = \frac{e^{w^Tx+b}}{1 + e^{w^Tx+b}} \\ p(y = 0 \ | \ x) = \frac{e^{-(w^Tx+b)}}{1 + e^{-(w^Tx+b)}} = \frac{1}{1 + e^{w^Tx+b}} \end{aligned} \]

于是我们可以确定学习准则了。我们取学习准则为 对数似然函数，于是参数的学习就是需要求解下式：

\[ \arg \max_{w, b} l(w, b) = \sum_{i = 1}^m \ln p(y_i\ | \ x_i; w, b) \]

而所谓的对数似然函数，就是 最大化类后验概率 使得样本属于真实标记的概率尽可能大。

我们将变量进行一定的变形：

\[ \begin{aligned} \begin{cases} \beta = (w; b) \\ \hat x = (x; 1) \\ \end{cases} &\to w^Tx + b = \beta^T\hat x \\ \begin{cases} p_1(\hat x; \beta) = p(y = 1 \ | \ \hat x; \beta) \\ p_0(\hat x; \beta) = p(y = 0 \ | \ \hat x; \beta) \\ \end{cases} &\to p(y_i\ | \ x_i; w, b) = y_i p_1(\hat x; \beta) + (1 - y_i) p_0(\hat x; \beta) \end{aligned} \]

于是上述对数似然函数就可以进行以下转化：

\[ \begin{aligned} l(w, b) &= l(\beta) \\ &= \sum_{i = 1}^m \ln \left [y_i p_1(\hat x; \beta) + (1 - y_i) p_0(\hat x; \beta) \right ] \\ &= \sum_{i = 1}^m \ln \left [y_i p(y = 1 \ | \ \hat x; \beta) + (1 - y_i) p(y = 0 \ | \ \hat x; \beta) \right ] \\ &= \sum_{i = 1}^m \ln \left [ y_i \frac{e^{\beta^T\hat x}}{1 + e^{\beta^T\hat x}} + (1-y_i) \frac{1}{1 + e^{\beta^T\hat x}} \right ] \\ &= \sum_{i = 1}^m \ln \left [ \frac{y_i \beta^T\hat x +1 -y_i}{1 + e^{\beta^T\hat x}} \right ] \\ &= \begin{cases} \sum_{i = 1}^m \ln \left ( \frac{1}{1 + e^{\beta^T\hat x}} \right ), & y_i = 0 \\ \sum_{i = 1}^m \ln \left ( \frac{e^{\beta^T\hat x}}{1 + e^{\beta^T\hat x}} \right ), & y_i = 1\\ \end{cases}\\ &= \sum_{i = 1}^m \ln \left ( \frac{\left(e^{\beta^T\hat x}\right)^{y_i}}{1 + e^{\beta^T\hat x}} \right ) \\ &= \sum_{i = 1}^m \left( y_i e^{\beta^T\hat x} - \ln({1 + e^{\beta^T\hat x}})\right ) \end{aligned} \]

进而从 极大似然估计 转化为：求解「极小化负的上述目标函数时」参数 \(\beta\) 的值：

\[ \arg \min_{\beta} l(\beta) = \sum_{i = 1}^m \left(- y_i e^{\beta^T\hat x} + \ln({1 + e^{\beta^T\hat x}})\right ) \]

优化算法

由于上式是关于 \(\beta\) 的高阶可导连续凸函数，因此我们有很多数值优化算法可以求得最优解时的参数值，比如梯度下降法、牛顿法、拟牛顿法等。我们以牛顿法 (Newton Method) 为例：

最优解 \(\beta ^*\) 定义为：

\[ \beta ^* = \arg \min_{\beta} l(\beta) \]

第 \(t+1\) 轮迭代解的更新公式：

\[ \beta ^{t+1} = \beta^t - \left( \frac{\partial^2{l(\beta)}}{\partial{\beta} \partial{\beta^T}} \right)^{-1} \frac{\partial{l(\beta)}}{\partial{\beta}} \]

其中 \(l(\beta)\) 关于 \(\beta\) 的一阶导、二阶导的推导过程如下：

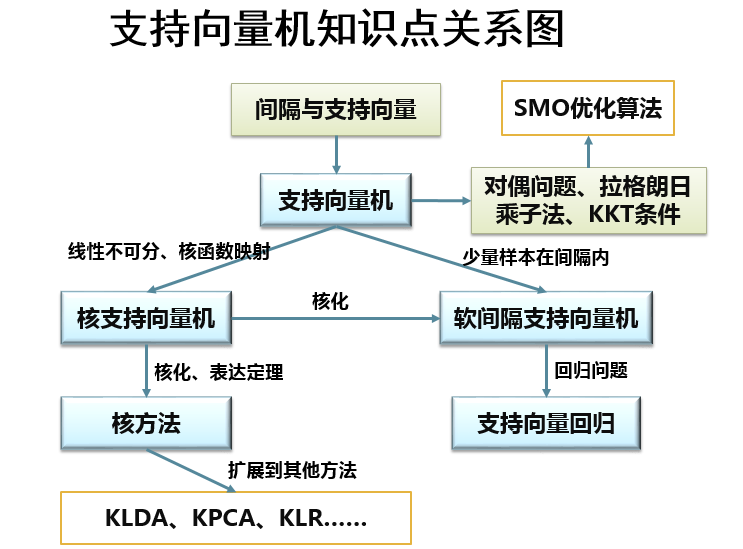
支持向量机

依然是分类学习任务。我们希望找到一个超平面将训练集中样本划分开来，那么如何寻找这个超平面呢？下面开始介绍。

本章知识点逻辑链：

间隔与支持向量

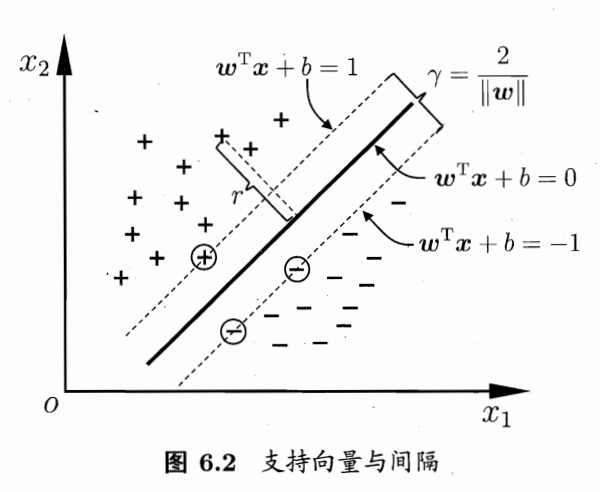
对于只有两个特征，输出只有两种状态的训练集而言，很显然我们得到如下图所示的超平面，并且显然应该选择最中间的泛化能力最强的那一个超平面：

我们定义超平面为：

\[ w^Tx+b = 0 \]

定义支持向量机为满足下式的样例：

\[ \begin{aligned} w^T+b&= 1 \\ w^T+b&=-1 \end{aligned} \]

很显然，为了求得这“最中间”的超平面，就是让异类支持向量机之间的距离尽可能的大，根据两条平行线距离的计算公式，可知间隔为：

\[ \gamma = \frac{2}{|| w ||} \]

于是最优化目标函数就是：

\[ \max_{w, b} \frac{2}{||w||} \]

可以等价转化为：

\[ \begin{aligned} &\min_{w, b} \frac{1}{2} ||w||^2 \\ &s.t. \quad y_i(w^Tx_i+b) \ge 1 \quad(i = 1,2,\cdots, m) \end{aligned} \]

这就是 SVM（support vector machine）的基本型

对偶问题

将上述 SVM 基本型转化为对偶问题，从而可以更高效的求解该最优化问题。

对偶转化推导

于是模型 \(f(x)\) 就是：

\[ \begin{aligned} f(x) &= w^Tx+b \\ &= \sum_{i = 1}^m\alpha_iy_ix_i^Tx+b \end{aligned} \]

其中参数 b 的求解可通过支持向量得到：

\[ y_if(x_i) = 1 \to y_i\left(\sum_{i = 1}^m\alpha_iy_ix_i^Tx+b \right)= 1 \]

由于原问题含有不等式约束，因此还需要满足 KKT 条件：

\[ \begin{cases} \alpha_i \ge 0&,\text{对偶可行性} \\ y_if(x_i) \ge 1&,\text{原始可行性} \\ \alpha_i(y_if(x_i)-1) = 0&,\text{互补松弛性} \end{cases} \]

对于上述互补松弛性：

若 \(\alpha_i > 0\)，则 \(y_if(x_i)=1\)，表示支持向量，需要保留
若 \(y_if(x_i)>1\)，则 \(\alpha_i = 0\)，表示非支持向量，不用保留

现在得到的对偶问题其实是一个二次规划问题，我们可以采用 SMO（Sequential Minimal Optimization）算法求解。具体略。

核函数

对原始样本进行升维，即 \(x_i \to \phi(x_i)\)，新的问题出现了，计算内积 \(\phi(x_i)^T \phi(x_i)\) 变得很困难，我们尝试解决这个内积的计算，即使用一个函数（核函数）来近似代替上述内积的计算结果，常用的核函数如下：

表格中的高斯核也就是所谓的径向基函数核 (Radial Basis Function Kernel, RBF 核)，其中的参数 \(\gamma=\frac{1}{2\sigma^2}\)，因此 RBF 核的表达式也可以写成：

\[ \kappa(x_i, x_j) = \exp(-\gamma \|x_i - x_j\|^2) \]

当 \(\gamma\) 较大时，\(\exp(-\gamma \|x_i - x_j\|^2)\) 的衰减速度会很快。这意味着只有非常接近的样本点才会有较高的相似度。此时，模型会更关注局部特征。并且会导致模型具有较高的复杂度，因为模型会更容易拟合训练数据中的细节和噪声，从而可能导致过拟合。
当 \(\gamma\) 较小时，\(\exp(-\gamma \|x_i - x_j\|^2)\) 的衰减速度会变慢。较远的样本点之间也可能会有较高的相似度。此时，模型会更关注全局特征。但此时模型的复杂度较低，容易忽略训练数据中的细节，从而可能导致欠拟合

软间隔与正则化

对于超平面的选择，其实并不是那么容易，并且即使训练出了一个超平面，我们也不知道是不是过拟合产生的，因此我们需要稍微减轻约束条件的强度，因此引入软间隔的概念。

我们定义软间隔为：某些样本可以不严格满足约束条件 \(y_i(w^Tx+b) \ge 1\) 从而需要尽可能减少不满足的样本个数，因此引入新的优化项：替代损失函数

\[ l_{\text{option}} \]

常见的平滑连续的替代损失函数为：

我们引入松弛变量 \(\xi_i\) 得到原始问题的最终形式：

\[ \min_{w, b,\xi_i} \quad \frac{1}{2}||w||^2+C\sum_{i = 1}^m \xi_i \]

支持向量回归

支持向量回归 (Support Vector Regression, SVR) 与传统的回归任务不同，传统的回归任务需要计算每一个样本的误差，而支持向量回归允许有一定的误差，即，仅仅计算落在隔离带外面的样本损失。

原始问题：

对偶问题：

KKT 条件：

预测模型：

核方法

通过上述：支持向量基本型、支持向量软间隔化、支持向量回归，三个模型的学习，可以发现最终的预测模型都是关于核函数与拉格朗日乘子的线性组合，那么这是巧合吗？并不是巧合，这其中其实有一个表示定理：

\[ h^*(x) = \sum_{i = 1}^m\alpha_i \kappa(x, x_i) \]

softmax

我们一般采用多分类+集成的策略来解决多分类的学习任务。具体的学习任务大概是：将多分类任务拆分为多个二分类任务，每一个二分类任务训练一个学习器；在测试数据时，将所有的分类器进行集成以获得最终的分类结果。这里有两个关键点：如何拆分多分类任务？如何集成二分类学习器？集成策略见第 8 章，本目主要介绍 多分类学习任务的拆分。主要有三种拆分策略：一对多、一对其余、多对多。对于 N 个类别而言：

一对一

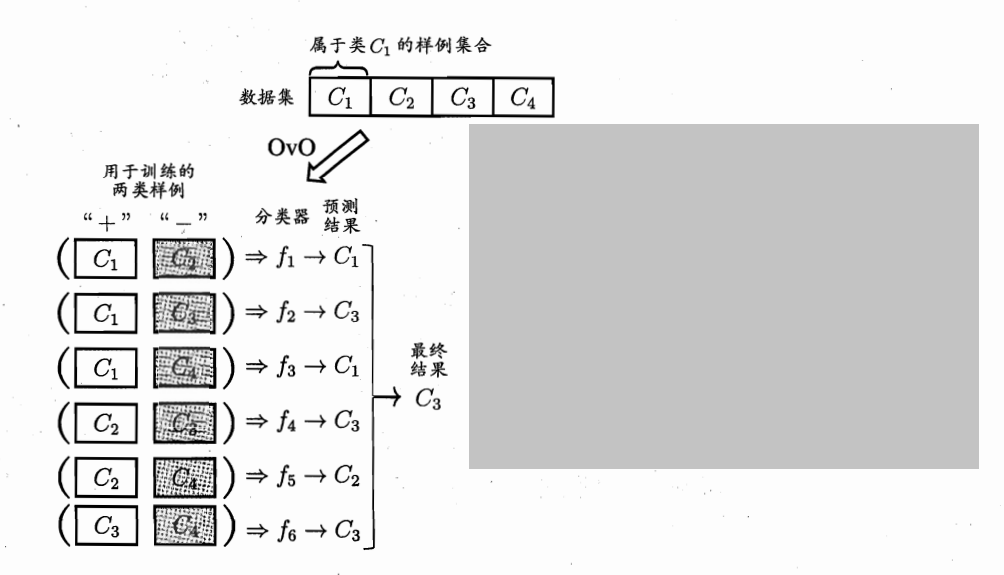
名称：One vs. One (OvO)
训练：需要对 N 个类别进行 \(\frac{N(N-1)}{2}\) 次训练，得到 \(\frac{N(N-1)}{2}\) 个二分类学习器
测试：对于一个样本进行分类预测时，需要用 \(\frac{N(N-1)}{2}\) 个学习器分别进行分类，最终分得的结果种类最多的类别就是样本的预测类别
特点：类别较少时，时间和内存开销往往更大；类别较多时，时间开销往往较小

一对其余

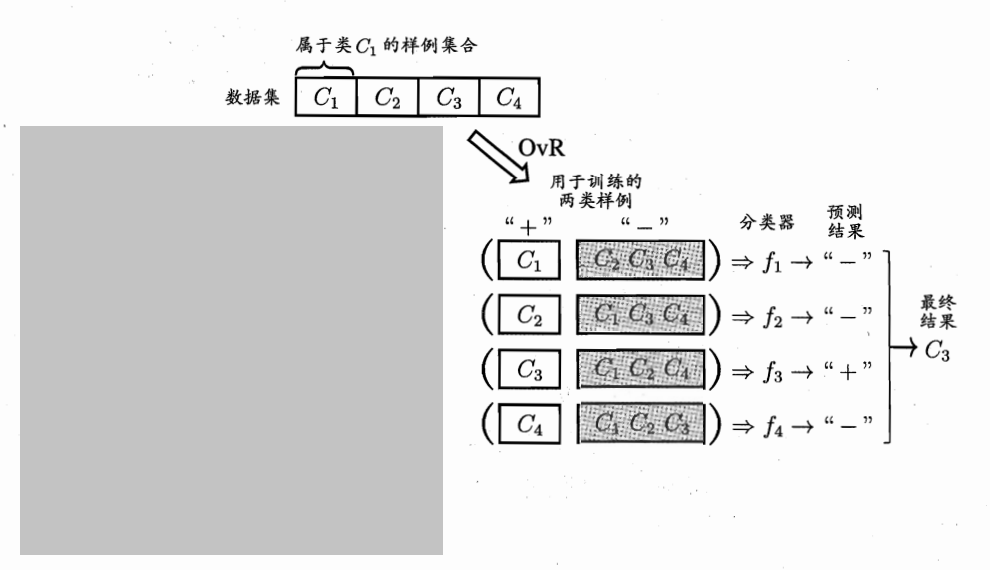
名称：One vs. Rest (OvR)
训练：需要对 N 个类别进行 \(N\) 次训练，得到 \(N\) 个二分类学习器。每次将目标类别作为正例，其余所有类别均为反例
测试：对于一个样本进行分类预测时，需要用 \(N\) 个学习器分别进行分类，每一个学习器显然只会输出二值，假定为正负。正表示当前样例属于该学习器的正类，反之属于反类。若 \(N\) 个学习器输出了多个正类标签，则还需通过执行度选择最终的类别。

多对多

名称：Many vs. Many (MvM)
训练（编码）：对于 N 个类别数据，我们自定义 M 次划分。每次选择若干个类别作为正类，其余类作为反类。每一个样本在 M 个二分类学习器中都有一个分类结果，也就可以看做一个 M 维的向量。m 个样本也就构成了 m 个在 M 维空间的点阵。
测试（解码）：对于测试样本，对于 M 个学习器同样也会有 M 个类别标记构成的向量，我们计算当前样本与训练集构造的 m 个样本的海明距离、欧氏距离，距离当前测试样本最近的点属于的类别，我们就认为是当前测试样本的类别。

softmax 函数

将当前测试样本属于各个类别的概率之和约束为 \(1\)。若共有 \(n\) 个输出，则将第 \(i\) 个输出 \(x_i\) 转化为 \([0,1]\) 取值范围的公式为：

\[ P_i =\frac{e^{x_i}}{\sum_{j = 1}^n e^{x_j}} \]