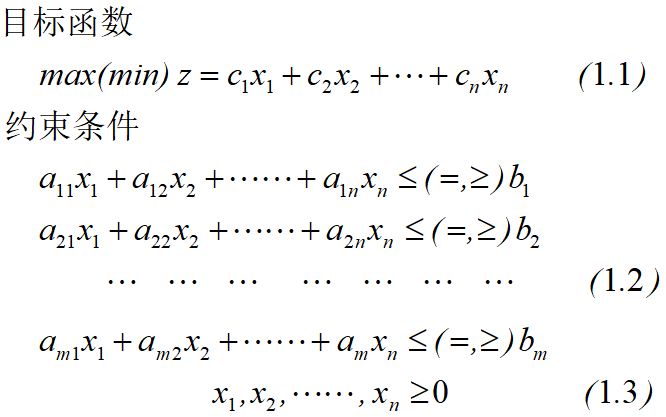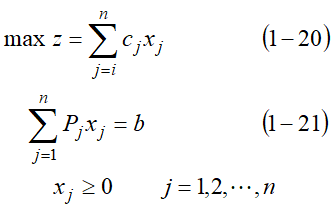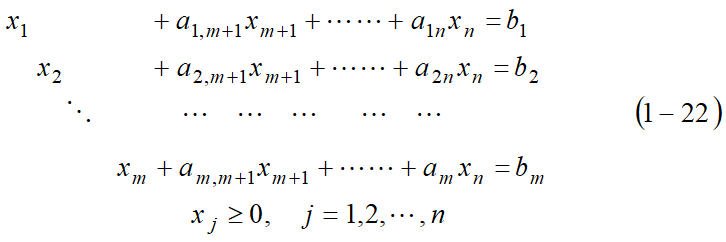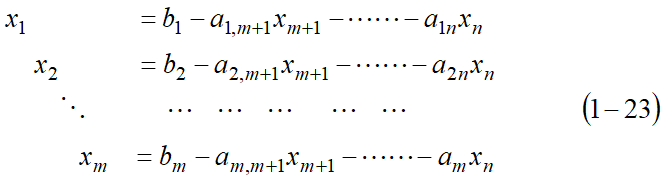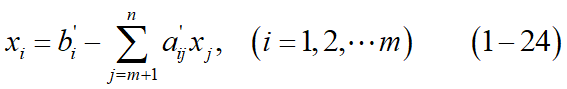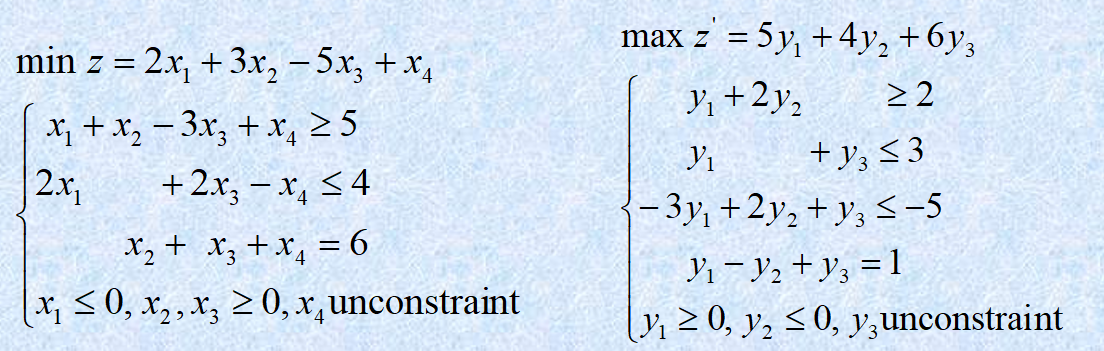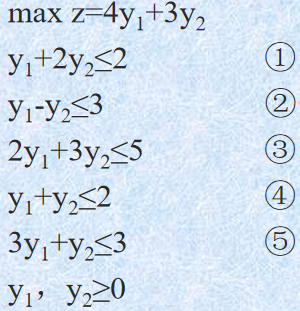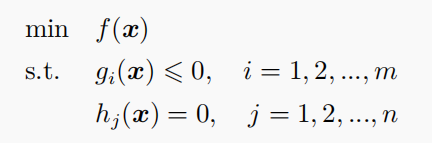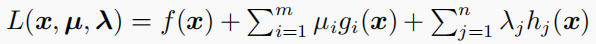跳转至

约束优化方法

线性规划

目标函数和约束函数都是线性函数。

线性规划问题和基本性质

线性规划问题

线性规划问题的一般形式

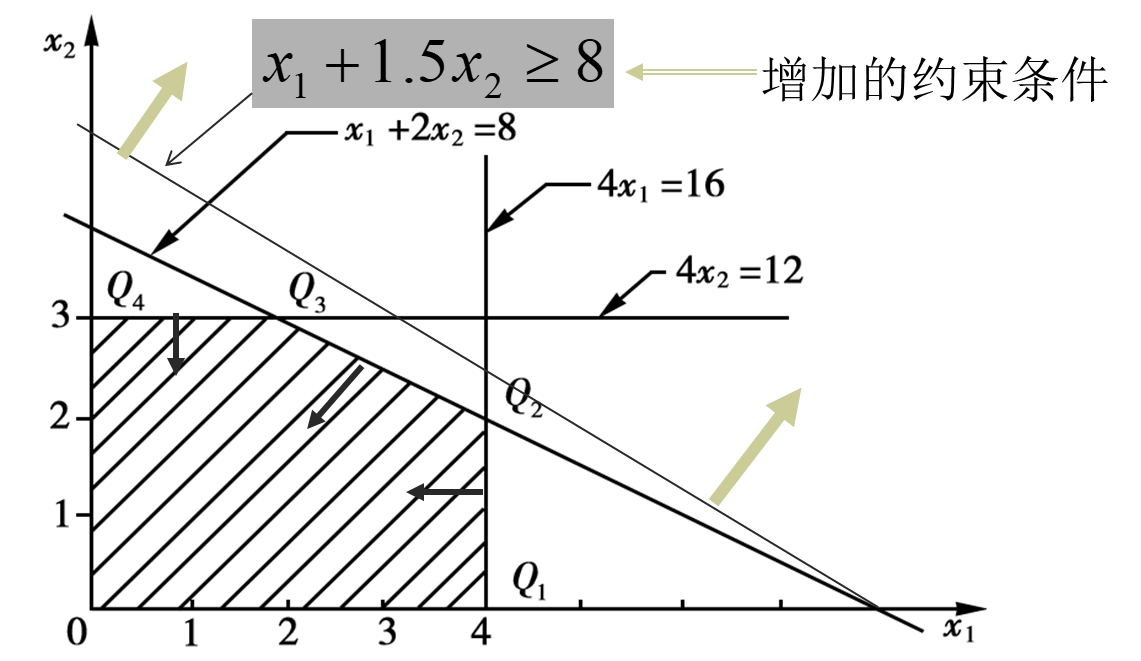
图解法

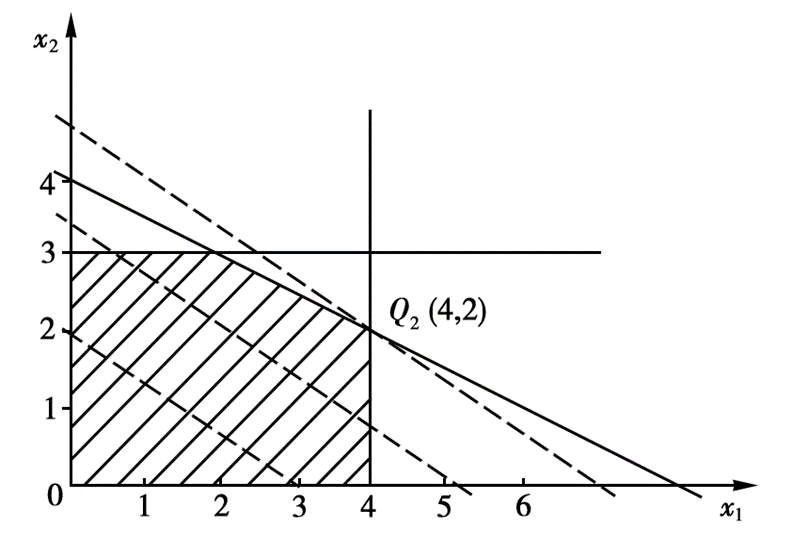
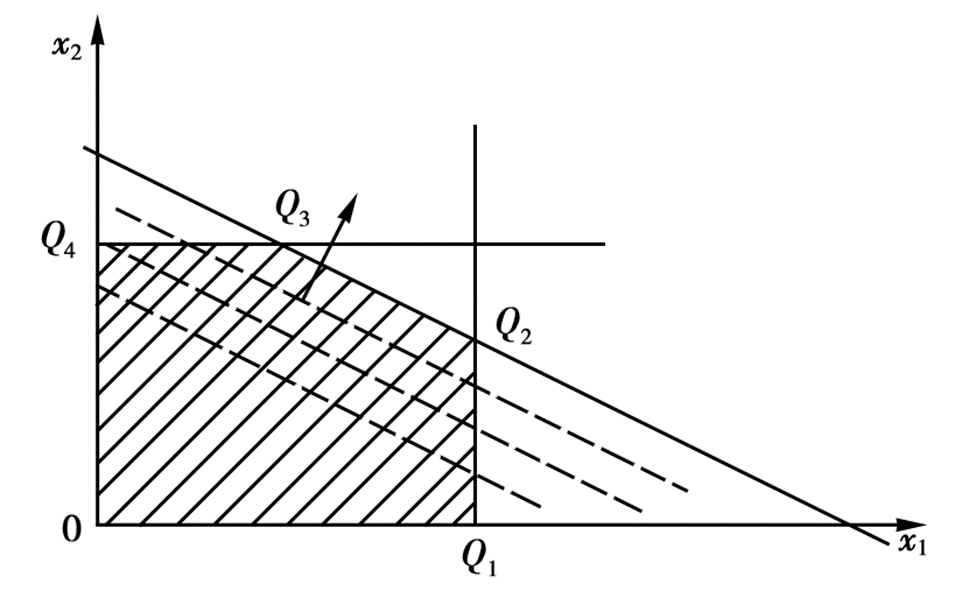
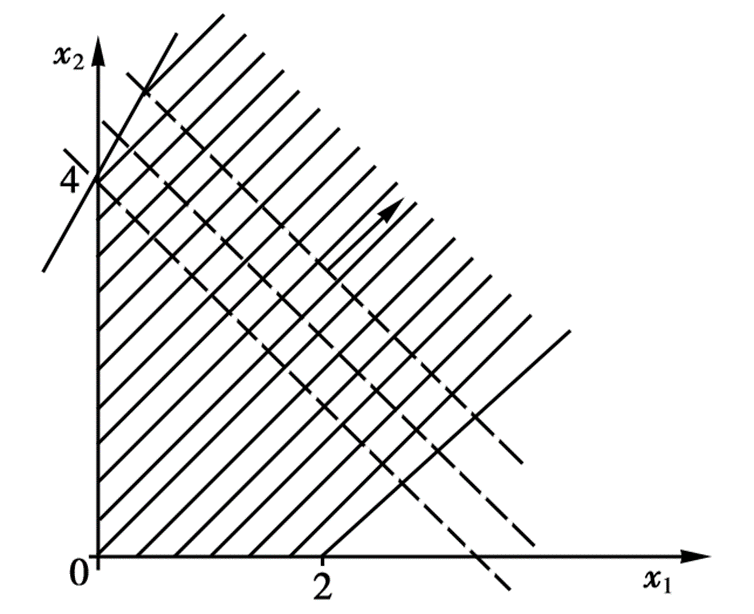
仅适用于二元变量 的线性规划问题。我们将所有的约束条件全部画到平面直角坐标系中构成一个可行域，然后将目标函数作为一条直线进行平移，直到与可行域初次有交点，则该交点就是最优解对应的点。当然不一定会有交点，一共分为四种情况：

刚好只有一个最优解

有无穷多最优解

有无界解

无可行解（可行域为空集）

基本性质

  1. 线性规划问题的可行域如果非空，则是一个凸集

    证明

    证明

  2. 如果线性规划问题有最优解，那么最优解可在可行域的顶点中确定

  3. 如果可行域有界且可行域只有有限个顶点，则问题的最优解必存在，并在这有限个顶点中确定

  4. 最优解可由最优顶点处的 有效约束 形成的方程组的解确定

线性规划的标准形

为什么要学习线性规划的标准形？

  • 我们要学习单纯形法来计算多维线性规划的最优解
  • 单纯形法需要线性规划的具有所谓的标准形

线性规划的标准形的定义：

  • 只含有线性等式约束和对变量的非负约束

一般线性规划转化为标准形的方法：

  1. 对于目标函数：需要将取 \(\max\) 通过 取相反数 转化为取 \(\min\)
  2. 对于约束条件：需要将不等式约束 松弛 转化为等式约束
    • 对于 \(\le\) 的不等式约束，等式左边加上非负新变量，从而转化为等式
    • 对于 \(\ge\) 的不等式约数，等式左边减去非负新变量，从而转化为等式
  3. 对于无约束的变量：需要将其转化为 两个新变量之差（可正可负），产生了一个新的等式，如果该无约束变量存在于目标函数中，还需要将目标函数中的该变量表示为两个新变量之差
举个例子

一般线性规划转化为标准形 - 演示

基本可行解

直接说结论：对于标准形的线性规划问题，其基本可行解就是凸集的顶点。

假设系数矩阵 \(A_{m, n}\)。基本可行解 \(\subset\) 基本解，而基本解的个数 \(\le C_{n}^{m}\)（因为分块矩阵 \(B_{m \times m}\) 不一定可逆）。其中基本可行解需要满足解序列元素非负。如果 基本变量 向量对应的解中含有 0 元素，称其为退化的基本可行解，产生退化的基本可行解的原因是存在可删除的约数条件。

最优解的性质

  • 若可行域有界，则线性规划问题的目标函数一定可以在其可行域的顶点上达到最优。

    证明（反证法）

    证明

  • 有时，目标函数可能在多个顶点处达到最大，这时在这些顶点的 凸组合 上也达到最大值，这时线性规划问题有无限多个最优解。

单纯形法

本目主要介绍一种常用的计算线性规划问题可行解的方法：单纯形法。其中，前三条 分别介绍单纯性方法计算步骤的理论可行性，第四条 具体介绍单纯形法的计算步骤与过程。

初始基可行解的确定

  1. 直接观察：直接看出系数矩阵中含有 \(m \times m\) 的单位矩阵，则选择该单位矩阵为初始基
  2. 加松弛变量：当所有的约束条件都是 \(\le\) 时，每一个约束条件都加一个非负的松弛变量，则这 \(m\) 个松弛变量的系数就对应了一个 \(m \times m\) 的单位矩阵，选择其为初始基即可
  3. 加非负的人工变量：求解方法与常规的线性规划问题不一样，见下述 2.2.3 条。
    • 对于 \(=\) 约束，我们在约束条件的左边加上非负人工变量
    • 对于 \(\ge\) 约束，我们先在约束条件的左边减去非负松弛变量，再在约束条件的左边加上非负的人工变量

最优性检验

符号说明

一、当前局面：已经计算出一个基本可行解

1.1 确定线性规划的目标

确定线性规划的目标

1.2 添加松弛变量

添加松弛变量

1.3 用非基变量线性表示基变量

用非基变量线性表示基变量

向量表示

二、最优性检验

最优性检验

  1. 唯一最优解 判别定理：对于 目标函数求解最大值 的情形。若 \(\forall j \in [m+1, n]\) 有 \(\sigma_j \le 0\) 则当前基本可行解 \(x^{(k)}\) 为最优解。

  2. 无穷多最优解 判别定理：在满足第一条所有的检验数非正的情况下，\(\exist j \in [m+1, n]\)，有 \(\sigma_j=0\)，则该线性规划问题有无穷多最优解。

    证明

    我们可以将任意一个检验数为 0 的非基变量与基变量进行置换得到新的一个基本可行解对应的目标函数值保持不变。于是下述凸组合内的可行解都是最优解

    \[ \begin{aligned} & x^{(k)} \\ & s.t. \begin{cases} k &\in& [m+1, n] \\ \sigma_k &=& 0 \end{cases} \end{aligned} \]

  3. 无界解 判别定理：pass

  4. 无解 判别定理：可行域为空集

2.2.3 计算新的基本可行解

对于 常规 的线性规划问题（初始基本可行解 \(x^{(0)}\) 可以直接找到）

  1. 向量方程法
    • 确定入基变量：选择目标函数中 系数最大的变量 作为入基变量，即将其对应的系数列向量与出基变量对应的系数列向量进行置换
    • 确定出基变量：线性表示基方程组以后，利用变量非负的特性找到入基变量刚好取 \(0\) 时对应的变量即为出基变量（示例的第二轮迭代中出基变量即为 \(x_5\)）
  2. 系数矩阵法
    • pass

对于 添加人工变量 的线性规划问题（初始基本可行解 \(x^{(0)}\) 不能直接找到，需要手动构造 \(x^{(0)}\)）

  1. 大 M 法：pass
  2. 两阶段法
    • 第一阶段：pass
    • 第二阶段：pass

2.2.4 单纯形表法

向量方程法：

实战演练

单纯形法的求解步骤 - 1

单纯形法的求解步骤 - 2

单纯形表法：

实战演练

实战演练

代码验算

对偶与对偶单纯形法

确定对偶问题

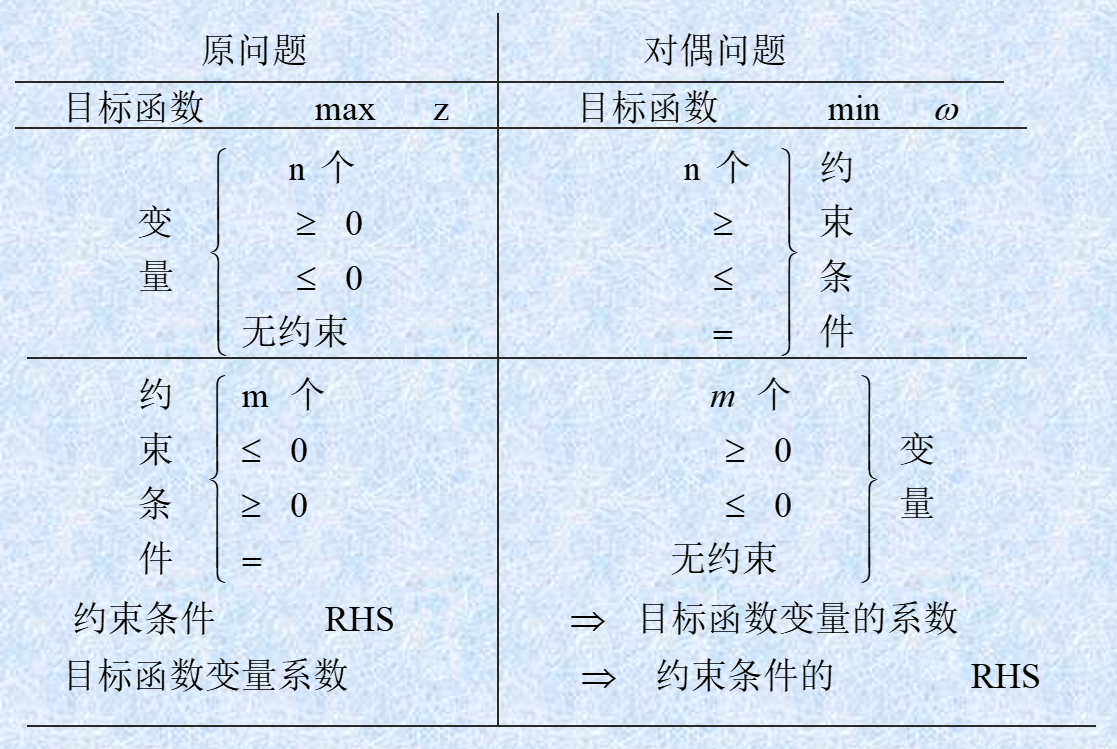
已知原问题的表达式，如何求解对偶问题的表达式？我们需掌握以下对偶转换规则：

转化规则

从上图不难发现，其实就是对线性规划的三个部分进行转换：目标函数、m 个约束条件、n 个自变量，下面分别进行文字介绍：

  1. 约束条件：从 m 个变为 n 个
    • 常量矩阵 中的元素为原问题中自变量的系数
    • 二元关系 的变化取决于转化方向
      • max to min：对偶问题约束条件的符号和原问题自变量的符号相同
      • min to max：对偶问题约束条件的符号和原问题自变量的符号相反
    • 线性约束 为原问题线性约束的转置
  2. 自变量：从 n 个变为 m 个
    • 二元关系 的变化同样取决于转化方向
      • max to min：对偶问题自变量的符号和原问题约束条件的符号相反
      • min to max：对偶问题自变量的符号和原问题约束条件的符号相同
  3. 目标函数：自元个数从 n 个变为 m 个
    • 变元的系数就是原问题中约束条件的常量矩阵对应的元素值
实战演练

实例

对偶定理

  • 对称性：对偶问题的对偶问题是原问题
  • 无界性：若原问题是无界解，则对偶问题无可行解
  • 对偶定理：若原问题有最优解，那么对偶问题也有最优解，且目标函数值相等
  • 互补松弛性：若原问题最优解为 \(x^*\)，对偶问题的最优解为 \(y^*\)，则有 \(x^* y_s=0,y^*x_s=0\)，其中 \(x_s,y_s\) 分别为原问题的松弛变量和对偶问题的松弛变量
实战演练

问题

对于上述问题，我们可以先写出其对偶问题：

对偶问题

显然的对于 \(y^*=(\frac{4}{5},\frac{3}{5})^T\)，上述 2,3,4 是取不到等号的，对应的 \(x^*=(-,0,0,0,-)^T\)。还剩两个变量 \(x_1,x_5\) 通过 1,5 两个不等式取等进行计算：

\[ \begin{aligned} x_1+3x_2 = 4\\ 2x_1+x_2 = 3 \end{aligned} \]

计算可得 \(x_1=1,x_5=1\)，于是原问题的最优解 \(x^*=(1, 0, 0, 0, 1)^T\)

对偶单纯形法

实战演练

实战演练

代码验算

二次规划

目标函数是二次函数，约束函数是线性函数。一般形式为：

\[ \begin{aligned} &\min \quad q(x) = \frac{1}{2}x^TGx + g^Tx \\ &s.t.\quad \begin{cases} a_i^Tx = b_i& , i\in S\\ a_i^Tx \ge b_i& , i \in M\\ \end{cases} \end{aligned} \]

本章将分别讨论约束函数「含有等式」和「含有不等式」两类二次规划问题。

等式约束二次规划

我们引入 拉格朗日方法 (Lagrange Method, 简称 LM)。此时可以用矩阵表示问题和约束条件，并且不加证明的给出最优解和对应乘子就是满足 KKT 条件下的解。

拉格朗日函数：

\[ L(x,\lambda) = \frac{1}{2}x^TGx+g^Tx -\lambda^T(A^Tx - b) \]

一阶必要条件：

\[ \begin{aligned} \frac{\partial L(x, \lambda) }{\partial x} &= Gx+g-A\lambda = 0 \\ \frac{\partial L(x, \lambda) }{\partial \lambda} &= A^x - b = 0 \end{aligned} \]

最优解的矩阵形式：

\[ \begin{aligned} \begin{bmatrix} G & -A \\ -A^T & 0 \end{bmatrix} \begin{bmatrix} x^* \\ \lambda^* \end{bmatrix} = - \begin{bmatrix} g \\ b \end{bmatrix} \end{aligned} \]

不等式约束二次规划

我们引入 有效集方法 (Active Set Method, 简称 ASM)。首先显然的最优解一定成立于等式约束，或成立于不等式取等。我们可以直接枚举每一种约束条件的组合（所有等式+枚举的不等式，并将不等式看做等式约束），然后判定当前的解是否满足没有选择的不等式约束。这种方法是可行的但是计算量极大。于是有效集方法应运而生。

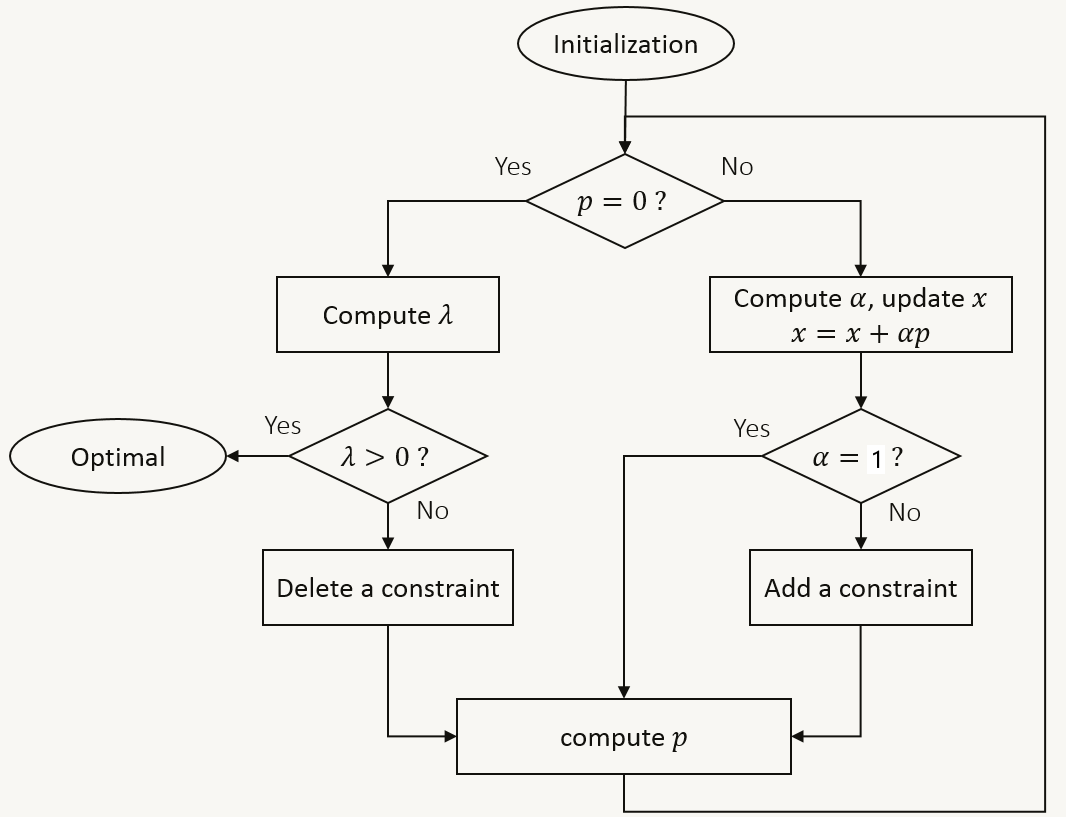
算法流程：

Primal ASM 算法

算法解析：

  • 计算初始可行点 \(x^{(0)}\)，可用线性规划中的大 M 法计算获得
  • 计算前进方向 \(p_k\)，通过求解等式约束二次规划子问题获得
  • 若 \(p_k = \bf{0}\)​，则 计算工作集约束 \(W_k\) 对应的所有拉格朗日乘子 \(\lambda_i\)
    • 若所有 \(\lambda_i \ge 0\)，则停止迭代，得到最优解 \(x^*=x^{(k)}\)
    • 若存在 \(\lambda_i < 0\)，则在工作集中剔除 \(\lambda_i\) 最小时对应的约束 \(a_j\)，得 \(W_{k+1}=W_k \setminus \set{a_j}\)
  • 若 \(p_k \ne \bf{0}\)，则 计算步长因子 \(\alpha_k\)，并置 \(x^{(k+1)} = x^{(k)} + \alpha_kp_k\)
    • 若 \(\alpha_k=1\)，则工作集不变，得 \(W_{k+1}=W_k\)
    • 若 \(\alpha_k < 1\)，则在工作集中添加 \(\alpha_k\) 最小时对应的约束 \(a_j\)，得 \(W_{k+1}=W_k \bigcup \set {a_j}\)

参考：

罚函数法

本章我们简单讨论 约束最优化问题 中，针对 等式约束 的「二次罚函数」算法。

拉格朗日乘子法

如果现在最优化问题不是单纯的 无约束最优化问题，而是增设了等式约束的 等式约束最优化问题，如何求解呢？我们引入 \(\text{Lagrange}\) 乘子法，将所有的等式约束都转化到目标函数中得到一个等价的无约束最优化问题，即：

对于这样的等式约束最优化问题：

\[ \begin{aligned} \min\quad& f(x)\\ \text{s.t.}\quad&c_i(x)= 0, i = 1,2,\cdots, m. \end{aligned} \]

引入拉格朗日乘子将其转化为无约束最优化问题，进而利用上述无约束最优化问题的求解策略进行求解：

\[ L(x,\lambda) = f(x) - \sum_{i = 1}^m\lambda_ic_i(x) \]

二次罚函数法

对于等式约束问题：

\[ \begin{aligned} &\min\quad f(x) \\ &s.t.\quad a_i(x) = 0,\ i = 1,2,..., p \end{aligned} \]

我们定义二次罚函数 \(P_E(x, \sigma)\)，其中 \(\sigma\) 为惩罚因子：

\[ P_E(x, \sigma) = f(x) + \frac{1}{2} \sigma\sum_{i = 1}^p a_i^2(x) \]

不加证明的给出结论：当惩罚因子 \(\to \infty\) 时，目标函数趋于最小值。下面给出算法流程：

等式约束的二次罚函数法

拉格朗日乘子法

目标函数：

目标函数

拉格朗日函数：

拉格朗日函数

KKT 条件：

KKT 条件

在实际求解时，我们只需要罗列上述 KKT 条件中的 (1) 和 (5)，另外三个显然不需要再罗列了。我们只需要对 \(m\) 个不等式约束条件对应的乘子进行是否为零的讨论即可，显然需要讨论 \(2^m\) 次。

后记

考试题型见 git 的历史，就不放这里丢人现眼了 🤣。