基础算法例题精讲

本文精选一些「基础算法」的例题并进行详细的原理讲解与代码实现。算法标签主要是「贪心、前缀和与差分、二分、递归」。题目来源主要是 Codeforces、洛谷、LeetCode。

一些做题小技巧：

贪心：善用枚举，可以从一两个元素开始考虑；
前缀和与差分：遇到区间修改操作时，应该立即想到其等价于对差分数组做端点修改操作；
二分：当按照题意进行正面模拟发现难以实现或者复杂度过高时，可以观察变量之间是否有单调性关系；
递归：搜索类题目，脑子里始终有一个搜索树，无论是具象化的树的题，还是可以抽象为树的搜索题；分治类题目，思考能不能先解决子问题，然后利用解决好的所有子问题来解决当前局面的问题。

为了提升阅读效率，我将题目的重要元信息单独罗列为了一张表格，可以按照自己的实际需求按需跳转阅读。

基础算法例题导读表（打 * 表示自己预估的难度）

标签 🏷	难度 🔥	链接 🔗	锚点 ⚓	策略 ⭐
贪心	CF 1200 *	蓝桥	通关	堆
贪心	CF 1500	CF	ABBC or BACB	翻转操作 $\xrightarrow{\text{看作}}$ 平移操作
贪心	CF 1800 *	力扣	子序列最大优雅度	反悔贪心
贪心	洛谷绿	洛谷	起床困难综合症	按位贪心
前缀和	CF 1600	CF	Decode	看到 01 数量相等，试着将 $0$ 转成 $-1$ 用前缀和做
差分	洛谷黄	洛谷	铺设道路	区间修改 $\xrightarrow{\text{差分}}$ 单点修改
二分	洛谷黄	洛谷	木材加工	二分答案找右边界
二分	CF 1400 *	AcWing	盖楼	二分答案找左边界、集合的思维
搜索	CF 1200 *	力扣	组合总和	组合型枚举
搜索	CF 1400 *	力扣	将石头分散的最少移动次数	排列型枚举
搜索	洛谷黄	洛谷	01 迷宫	连通分量板子题
搜索	CF 1500 *	AcWing	扩展字符串	trick：预处理设置上限
分治	CF 1400 *	AcWing	随机排列	逆序数板子题

通关

OJ：蓝桥

题意：给定一棵含有 $n$ 个结点的树和一个初始价值，树中每个结点代表一个关卡，每个关卡有「通过最低需求价值」和「通过奖励价值」两个属性。只有通过了父结点关卡才能继续挑战子结点关卡。现在从根结点开始尝试通关，问应该如何选择通关顺序使得通过的关卡数最多？给出最多通关的关卡数。

思路：我们每次贪心地选择需求价值最小的关卡进行闯关即可。可以通过二叉堆来实现。

时间复杂度：$O(n \log n)$

PythonC++

from heapq import *

n, have = map(int, input().split())
g = [[] for _ in range(n + 1)]

for i in range(1, n + 1):
    fa, get, need = map(int, input().split())
    g[fa].append((need, -get, i))

ans = 0
h = [g[0][0]]
heapify(h)  # 默认小根堆
while h:
    need, neg_get, now = heappop(h)
    if have < need:
        break
    have += -neg_get
    ans += 1
    for ch in g[now]:
        heappush(h, ch)

print(ans)

#include <iostream>
#include <queue>
using namespace std;
using ll = long long;

int main() {
    int n;
    ll have;
    cin >> n >> have;

    struct Node {
        int fa, get, need;
        bool operator<(const Node& t) const {
            if (need == t.need) {
                return get < t.get;
            }
            return need > t.need;
        }
    };

    vector<Node> g[n + 1];
    for (int i = 1; i <= n; i++) {
        int fa, get, need;
        cin >> fa >> get >> need;
        g[fa].push_back({i, get, need});
    }

    priority_queue<Node> q;  // 默认大根堆
    q.push({g[0][0]});
    int ans = 0;
    while (q.size()) {
        auto [now, get, need] = q.top();
        q.pop();
        if (have < need) {
            break;
        }
        ans++;
        have += get;
        for (auto ch: g[now]) {
            q.push(ch);
        }
    }

    cout << ans << "\n";

    return 0;
}

ABBC or BACB

OJ：CF

题意：现在有一个由 A 和 B 两种字符组成的字符串 $s\ (1\le|s|\le2\cdot 10^5)$。操作一，可以将 AB 转化为 BC；操作二，可以将 BA 转化为 CB。问最多可以执行上述操作多少次。给出最多操作次数。

思路：

容易发现，题意中的两种翻转操作可以转化为平移操作。即，两种操作都可以看做是对 B 字符的移动，操作一是向左移动，操作二是向右移动。于是题目就转化为了怎么选择每一个 B 字符的移动方向可以尽可能多的经过 A 字符；
不难发现，如果字符串的边缘有 B 字符或者有至少两个连续的 B 字符，那么所有的 A 字符都能被经过。反之，就是单独的 B 字符将一个完整的 A 串切割开来的情景，此时就是小学学到的线段模型，选择长度最短的 A 子串不经过即可。

时间复杂度：$O(n)$

PythonC++

T = int(input())
for _ in range(T):
    s = input()
    cnt_A = s.count('A')
    if s[0] == 'B' or s[-1] == 'B' or s.count('BB'):
        print(cnt_A)
    else:
        min_len_A = len(s)  # 最短 A 串长度
        i = 0
        while i < len(s):
            if s[i] == 'A':
                j = i
                while j < len(s) and s[j] == 'A':
                    j += 1
                min_len_A = min(min_len_A, j - i)
                i = j
            else:
                i += 1
        print(cnt_A - min_len_A)

#include <algorithm>
#include <climits>
#include <iostream>
using namespace std;

void solve() {
    string s;
    cin >> s;

    int cnt_A = count(s.begin(), s.end(), 'A');

    auto check_bb = [](string& s) -> bool {
        for (int i = 1; i < s.size(); i++) {
            if (s[i] == s[i - 1] && s[i] == 'B') {
                return true;
            }
        }
        return false;
    };

    if (s[0] == 'B' || s[s.size() - 1] == 'B' || check_bb(s)) {
        cout << cnt_A << "\n";
        return;
    }

    int min_len_A = INT_MAX / 2;  // 最短 A 串长度
    for (int i = 0; i < s.size(); ) {
        if (s[i] == 'A') {
            int j = i;
            while (j < s.size() && s[j] == 'A') {
                j++;
            }
            min_len_A = min(min_len_A, j - i);
            i = j + 1;
        } else {
            i++;
        }
    }
    cout << cnt_A - min_len_A << "\n";
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

同类题推荐：

CF 1300 * | 力扣 | 修改后的最大二进制字符串 - (leetcode.cn)

子序列最大优雅度

OJ：力扣

题意：给定长度为 $n \ (1\le n \le 10^5)$ 的二元组序列，二元组表示每一个元素的价值与种类。现在需要从中寻找一个长度为 $k$ 的子序列使得该序列「所有物品价值之和 + 物品种类数的平方」的值最大。返回该最大值。

思路：我们采用反悔贪心的思路。首先按照物品本身价值进行降序排序并选择前 $k$ 个物品作为集合 $S$，然后按顺序枚举剩下的物品进行替换决策。当且仅当集合 S 有物品的类别重复且剩下物品的类别不存在于集合 $S$ 中才有可能让答案更大。

时间复杂度：$O(n \log n)$

PythonC++

class Solution:
    def findMaximumElegance(self, items: List[List[int]], k: int) -> int:
        n = len(items)
        items.sort(key=lambda x: -x[0])

        # 贪心
        val, cat = 0, 0
        cnt = [0] * (n + 1)
        rep = []
        for i in range(k):
            v, c = items[i]
            val += v
            cat += cnt[c] == 0
            cnt[c] += 1
            if cnt[c] > 1:
                rep.append(v)

        # 反悔
        ans = val + cat ** 2
        for i in range(k, n):
            v, c = items[i]
            if cnt[c] == 0 and len(rep):
                val -= rep.pop()
                val += v
                cat += 1
                cnt[c] += 1
                ans = max(ans, val + cat ** 2)

        return ans

using ll = long long;

class Solution {
public:
    ll findMaximumElegance(vector<vector<int>>& items, int k) {
        int n = items.size();
        sort(items.rbegin(), items.rend());

        // 贪心
        ll val = 0, cat = 0;
        vector<int> cnt(n + 1, 0);
        vector<int> rep;
        for (int i = 0; i < k; i++) {
            int v = items[i][0], c = items[i][1];
            val += v;
            cat += !cnt[c];
            cnt[c] += 1;
            if (cnt[c] > 1) {
                rep.push_back(v);
            }
        }

        // 反悔
        ll ans = val + cat * cat;
        for (int i = k; i < n; i++) {
            int v = items[i][0], c = items[i][1];
            if (!cnt[c] && !rep.empty()) {
                val += v;
                val -= rep.back();
                rep.pop_back();
                cnt[c] += 1;
                cat += 1;
                ans = max(ans, val + cat * cat);
            }
        }

        return ans;
    }
};

同类题推荐：

原料采购 | 第 16 届蓝桥杯 Python A 组最后一题

起床困难综合症

OJ：洛谷

题意：给定 $n\ (2 \le n \le 10^5)$ 个操作对，每个操作对包含一个位运算（「按位与、按位或、按位异或」三者之一）和一个操作数 $t\ (0 \le t \le 10^9)$。现在需要选择一个初始值 $num\in{\{0, 1, \cdots,m\}},\ (2 \le m \le 10^9)$，使得 $num$ 经过这 $n$ 次二元运算后得到的结果最大。输出最大运算结果。

思路：

由于三种操作是相邻无关的，因此我们可以按每一个二进制位单独考虑。对于第 $i$ 位，初始值为 $0$ 或 $1$ 在经过 $n$ 次运算后均有可能得到 $0$ 和 $1$，因此我们有 $4$ 种情况需要讨论，每种情况贪心地选择最优即可；
而为了让结果最大，我们需要从高位开始枚举。因为当初始值填 $1$ 更优时，如果先填低位，可能会导致高位填不了 $1$ 从而得不到最大的答案值。

时间复杂度：$O(n)$

PythonC++

n, m = map(int, input().strip().split())

x, y = 0, -1
for _ in range(n):
    inp = input().strip().split()
    op, t = inp[0], int(inp[1])
    if op == "AND":
        x &= t
        y &= t
    elif op == "OR":
        x |= t
        y |= t
    else:
        x ^= t
        y ^= t

ans, num = 0, 0
for i in range(30, -1, -1):
    a, b = (x >> i) & 1, (y >> i) & 1
    # 下列四种情况可以简化，为了逻辑清晰性就不简化了
    if a and b:
        ans |= 1 << i
    elif a and not b:
        ans |= 1 << i
    elif not a and b:
        if num | (1 << i) <= m:
            num |= 1 << i
            ans |= 1 << i
    else:
        pass

print(ans)

#include <iostream>
#include <vector>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    vector<pair<string, int>> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i].first >> a[i].second;
    }

    // 预处理所有可能的结果
    int x = 0, y = -1;
    for (int i = 0; i < n; i++) {
        auto [op, t] = a[i];
        if (op == "AND") {
            x &= t;
            y &= t;
        } else if (op == "OR") {
            x |= t;
            y |= t;
        } else {
            x ^= t;
            y ^= t;
        }
    }

    // 从高位开始贪心选择
    int ans = 0, num = 0;
    for (int i = 30; i >= 0; i--) {
        int a = (x >> i) & 1, b = (y >> i) & 1;
        if (a == 1 && b == 0) {
            ans |= 1 << i;
        } else if (a == 0 && b == 1 && ((num | (1 << i)) <= m)) {
            num |= 1 << i;
            ans |= 1 << i;
        } else if (a == 1 && b == 1) {
            ans |= 1 << i;
        }
    }

    cout << ans << "\n";

    return 0;
}

Decode

OJ：CF

题意：给定一个 01 字符串 $s\ (1\le \lvert s \rvert \le 2\cdot10^5)$，计算 $s$ 的所有子区间中 01 数量相等的子串数量，将结果对 $10^9+7$ 取模。

思路：

下标从 $1$ 开始，采用枚举右维护左的策略来枚举所有合法子串。即统计「以 $s_i\ (i\in [1,n])$ 结尾的合法子串」在所有区间中的数量，最朴素的做法就是利用前缀和，枚举 $j \in [0,i-1]$ 并统计区间长度是区间和两倍的子串数量，但这是 $O(n^2)$ 的，无法通过本题；
引入 01 串的前缀和维护 trick：当 s[i] == '0' 时，将其记作 -1，当 s[i] == '1' 时，仍然记作 1。这样我们就可以将「枚举 $j$ 寻找合法区间个数」的操作转化为「统计 pre[j] == pre[i] 个数」的操作，而这显然可以通过哈希表/桶/红黑树来维护，从而将枚举 $j$ 的时间复杂度从 $O(n)$ 降至 $O(1)$ 或 $O(\log n)$；
容易发现，一个合法的 $j$ 对应的子串 $s_{j+1\sim i}$ 存在于 $(j+1)\cdot (n-i+1)$ 个区间中，也就意味着对最终答案也贡献了这么多，因此我们在枚举 $i$ 时只需要统计所有合法的 $j$ 即可，而这在上一步就已经完成了。

时间复杂度：$O(n)$

PythonC++

from collections import defaultdict

T = int(input().strip())
OUTs = []
for _ in range(T):
    s = input().strip()
    n = len(s)

    pre = [0] * (n + 1)
    for i in range(n):
        pre[i + 1] = pre[i] + (-1 if s[i] == '0' else 1)

    ans = 0
    cnt = defaultdict(int)
    cnt[0] = 1
    for i in range(1, n + 1):
        ans = (ans + cnt[pre[i]] * (n - i + 1)) % (10**9 + 7)
        cnt[pre[i]] += i + 1

    OUTs.append(ans)

print('\n'.join(map(str, OUTs)))

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
using ll = long long;

const int MOD = 1e9 + 7;

void solve() {
    string s;
    cin >> s;

    int n = s.size();
    vector<int> pre(n + 1);
    for (int i = 0; i < n; i++) {
        pre[i + 1] = pre[i] + (s[i] == '0' ? -1 : 1);
    }

    int ans = 0;
    unordered_map<int, ll> cnt;
    cnt[0] = 1;
    for (int i = 1; i <= n; i++) {
        ans = (1ll * ans + cnt[pre[i]] * (n - i + 1)) % MOD;
        cnt[pre[i]] += i + 1;
    }

    cout << ans << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

同类题推荐：

CF 1300 * | 截断数组 | AcWing - (www.acwing.com)

铺设道路

OJ：洛谷

题意：给定一个含有 $n\ (1 \le n \le 10^5)$ 个数序列 $a\ (0\le a_i\le 10^4)$，每次操作可以让一个区间内所有数减一，前提是区间中的数都要 $\ge1$。输出将所有的数全部都减到 $0$ 的最小操作次数。

思路：看到区间操作，首先想到差分。于是区间操作就等价于修改差分数组 b，那么区间的最小操作次数就等价于 b[l]--, b[r+1]++ 的最小操作次数。由于 b[r+1]++ 不是必须的（因为右端点不一定需要存在，即给序列的整个右半段执行区间操作），因此本题的答案就是 $\sum_{i=0}^{n-1}b_i\cdot \mathbb I(b_i>0)$。

时间复杂度：$O(n)$

PythonC++

n = int(input())
a = list(map(int, input().split()))

ans = a[0]
for i in range(1, n):
    ans += max(0, a[i] - a[i - 1])

print(ans)

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    int ans = 0;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        if (!i) {
            ans += a[i];
        } else {
            ans += max(0, a[i] - a[i - 1]);
        }
    }

    cout << ans << "\n";

    return 0;
}

同类题推荐：

CF 1500 * | 增减序列 | AcWing - (www.acwing.com)

木材加工

OJ：洛谷

题意：给定 $n\ (1\le n \le 10^5)$ 根木头，现在需要将这些木头切成 $k\ (1\le k \le 10^8)$ 段等长的小段，问小段的最大长度是多少。

思路：小段长度越长，可切出的小段就越少，具备单调性，那么直接二分小段长度，找到最大的小段长度值使得可切出的小段个数 $\ge k$ 即可。

时间复杂度：$O(n\log k)$

PythonC++

n, k = map(int, input().strip().split())
a = [int(input()) for _ in range(n)]

def chk(v: int) -> bool:
    s = 0
    for x in a:
        s += x // v
    return s >= k

l, r = 0, max(a)
while l < r:
    mid = (l + r + 1) >> 1
    if chk(mid):
        l = mid
    else:
        r = mid - 1

print(l)

#include <iostream>
#include <vector>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    ll n, k;
    cin >> n >> k;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    auto chk = [&](int v) -> bool {
        ll cnt = 0;
        for (int i = 0; i < n; i++) {
            cnt += a[i] / v;
        }
        return cnt >= k;
    };

    int l = 0, r = 1e8;
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if (chk(mid)) {
            l = mid;
        } else {
            r = mid - 1;
        }
    }

    cout << r << "\n";

    return 0;
}

盖楼

OJ：AcWing

题意：给定 $n,m,x,y\ (1\le n,m\le10^9,2\le x,y< 30000)$，其中 $x$ 和 $y$ 均为质数。现在有一个排列数数组，需要将数组中的部分数字分配给两个人。其中一个人需要 $n$ 个数且不允许给它能被 $x$ 整除的数，另一个人需要 $m$ 个数且不允许给它能被 $y$ 整除的数。问这个排列数数组的大小最小是多少。

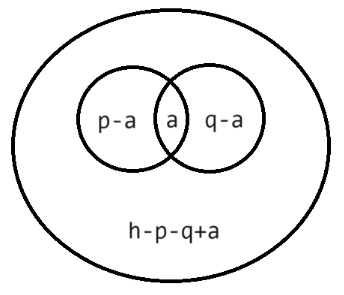
思路：假设排列数共有 $h$ 个，能被 $x$ 整除的数有 $p$ 个，能被 $y$ 整除的数有 $q$ 个，能同时被 $x$ 和 $y$ 整除的数有 $a$ 个。一种贪心的分配策略就是，优先将自己不要的数分配给对方，然后再从 $h-p-q+a$ 中分配。由于 $h$ 越大，可分配的数字就越多，为了找到最小的 $h$，套二分查找左边界的板子即可。

时间复杂度：$O(\log n)$

PythonC++

n, m, x, y = map(int, input().strip().split())

def chk(h: int) -> bool:
    p = h // x
    q = h // y
    a = h // (x * y)
    return h - p - q + a < max(0, n - (q - a)) + max(0, m - (p - a))

l, r = 0, 10**15
while l < r:
    mid = (l + r) >> 1
    if chk(mid):
        l = mid + 1
    else:
        r = mid

print(l)

#include <iostream>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m, x, y;
    cin >> n >> m >> x >> y;

    auto chk = [&](ll h) -> bool {
        ll p = h / x, q = h / y, a = h / (x * y);
        return h - p - q + a < max(0ll, n - (q - a)) + max(0ll, m - (p - a));
    };

    ll l = 1, r = 1e15;
    while (l < r) {
        ll mid = (l + r) >> 1;
        if (chk(mid)) {
            l = mid + 1;
        } else {
            r = mid;
        }
    }

    cout << r << "\n";

    return 0;
}

同类题推荐：

组合总和

OJ：力扣

题意：给定一个含有 $n\ (1\le n \le 30)$ 个不重复元素的序列，问如何选取其中的元素（可重复选），能够使得选出的数字总和为 $\text{target}\ (1\le \text{target}\le 40)$。给出所有具体选数方案（不考虑数字的选择顺序）。

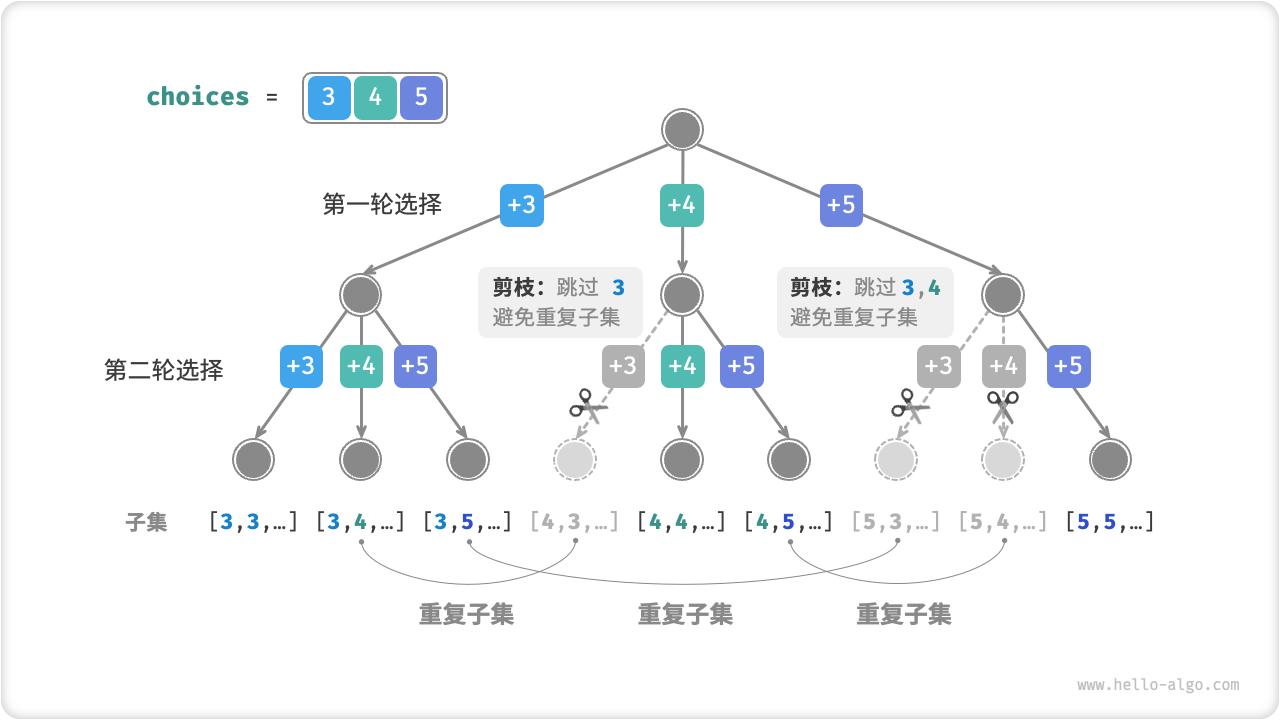
思路：不考虑顺序就是组合数，即组合型搜索经典例题。在枚举序列中的元素时，需要从上一次枚举结束的位置开始，防止方案重复（也可以理解为剪枝操作）。下图对组合型搜索进行了可视化：

时间复杂度：不太会计算时间复杂度，但是在本题的数据量下通过剪枝可以很快的算出方案。具体复杂度推导见三种方法：选或不选/枚举选哪个/完全背包预处理+可行性剪枝 - (leetcode.cn)。

PythonC++

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        n = len(candidates)
        ans = []
        path = []

        def dfs(remain: int, idx: int) -> None:
            if remain < 0:
                return
            elif remain == 0:
                ans.append(path.copy())  # 对于列表，append 的是一个引用，所以要加 copy
                return
            for i in range(idx, n):
                path.append(candidates[i])
                dfs(remain - candidates[i], i)
                path.pop()

        dfs(target, 0)

        return ans

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        int n = candidates.size();
        vector<vector<int>> ans;
        vector<int> path;

        function<void(int, int)> dfs = [&](int remain, int idx) {
            if (remain < 0) {
                return;
            } else if (remain == 0) {
                ans.push_back(path);
                return;
            }
            for (int i = idx; i < n; i++) {
                path.push_back(candidates[i]);
                dfs(remain - candidates[i], i);
                path.pop_back();
            }
        };

        dfs(target, 0);

        return ans;
    }
};

将石头分散的最少移动次数

OJ：力扣

题意：给定一个 $3\times 3$ 的矩阵 $g$，其中数字总和为 $9$ 且 $g[i][j] \ge 0$，现在需要将其中 $>1$ 的数字沿着直角边移动到值为 $0$ 的位置上使得最终矩阵全为 $1$，输出最小的总移动距离。

思路：

记 $0$ 为空位，假设有 $k$ 个空位，那么就一定有 $k$ 个 $1$ 可以移动，因此这道题本质上就是 $k$ 个空位与 $k$ 个 $1$ 的匹配问题。为了不漏掉任何一种匹配方式，我们直接全排列枚举空位或者 $1$ 的位置即可，此处我们选择前者；
Python 和 C++ 都内置了全排列的库函数：
- C++ 的全排列枚举库函数为 std::next_permutation(ItFirst, ItEnd)，每次返回刚好比当前排列字典序大的排列；
- Python 的全排列枚举库函数为 itertools.permutations(Iterable)，按照字典序一次性返回所有排列。

时间复杂度：$O(9\times 9!)$

PythonPython 库函数C++C++ 库函数

class Solution:
    def minimumMoves(self, g: List[List[int]]) -> int:
        a = []  # 存 0 的位置
        b = []  # 存 1 的位置
        for i in range(3):
            for j in range(3):
                if g[i][j] == 0:
                    a.append((i, j))
                elif g[i][j] > 1:
                    b.extend([(i, j)] * (g[i][j] - 1))

        ans = 1000
        n = len(a)
        vis = [False] * n

        def dfs(i: int, now: int) -> None:
            if i == n:
                nonlocal ans
                ans = min(ans, now)
                return

            # i 是 1，j 是空位
            for j in range(n):
                if vis[j]:
                    continue
                vis[j] = True
                dfs(
                    i + 1,
                    now + abs(a[j][0] - b[i][0]) + abs(a[j][1] - b[i][1])
                )
                vis[j] = False

        dfs(0, 0)

        return ans

from itertools import permutations

class Solution:
    def minimumMoves(self, g: List[List[int]]) -> int:
        a = []
        b = []
        for i in range(3):
            for j in range(3):
                if g[i][j] == 0:
                    a.append((i, j))
                elif g[i][j] > 1:
                    for _ in range(g[i][j] - 1):
                        b.append((i, j))

        ans = 1000
        for p in permutations(a):
            now = 0
            for i, (x, y) in enumerate(p):
                now += abs(x - b[i][0]) + abs(y - b[i][1])
            ans = min(ans, now)

        return ans

class Solution {
public:
    int minimumMoves(vector<vector<int>>& g) {
        vector<array<int, 2>> a, b;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (g[i][j] == 0) {
                    a.push_back({i, j});
                } else if (g[i][j] > 1) {
                    for (int _ = 0; _ < g[i][j] - 1; _++) {
                        b.push_back({i, j});
                    }
                }
            }
        }

        int ans = 1000;
        int n = a.size();
        vector<bool> vis(n);

        auto dfs = [&](auto&& dfs, int i, int now) -> void {
            if (i == n) {
                ans = min(ans, now);
                return;
            }
            for (int j = 0; j < n; j++) {
                if (vis[j]) {
                    continue;
                }
                vis[j] = true;
                dfs(
                    dfs,
                    i + 1,
                    now + abs(a[j][0] - b[i][0]) + abs(a[j][1] - b[i][1])
                );
                vis[j] = false;
            }
        };

        dfs(dfs, 0, 0);

        return ans;
    }
};

class Solution {
public:
    int minimumMoves(vector<vector<int>>& g) {
        vector<array<int, 2>> a, b;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (g[i][j] == 0) {
                    a.push_back({i, j});
                } else if (g[i][j] > 1) {
                    for (int _ = 0; _ < g[i][j] - 1; _++) {
                        b.push_back({i, j});
                    }
                }
            }
        }

        int ans = 1000;
        do {
            int now = 0;
            for (int i = 0; i < a.size(); i++) {
                now += abs(a[i][0] - b[i][0]) + abs(a[i][1] - b[i][1]);
            }
            ans = min(ans, now);
        } while (next_permutation(a.begin(), a.end()));

        return ans;
    }
};

扩展字符串

OJ：AcWing

题意：给定一种字符串构造方法，进行 $q\ (1\le q\le 10)$ 次查询，每次询问第 $n\ (0\le n\le 10^5)$ 个字符串中第 $k\ (1\le k \le 10^{18})$ 个字符是什么（字符串下标从 $1$ 开始）。如果越界输出 '.'。字符串构造方法如下：

$s_0 = $ DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB；
$s_i = $ DKER EPH VOS GOLNJ UKLMH QHNGLNJ A $+s_{i−1}+$ AB CPH VOS FSQVB DLMM VOS QHNG A $+s_{i−1}+$ AB。

思路：

可以发现字符串构造方法类似二叉递归的形式，我们预处理每一个状态的字符串长度后直接递归搜索即可；
由于 $n$ 的上限很大，直接存储每一个状态的长度肯定会炸（C++ 炸 long long，Python 会因为高精炸时空）。注意到询问的下标索引不超过 $10^{18}$，因此我们在预处理时给每一个状态的字符串长度设置上限即可。

时间复杂度：$O(qn)$

PythonC++

import sys
sys.setrecursionlimit(100000)

s = "DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB"
t0 = "DKER EPH VOS GOLNJ UKLMH QHNGLNJ A"
t1 = "AB CPH VOS FSQVB DLMM VOS QHNG A"
t2 = "AB"
l0, l1, l2 = len(t0), len(t1), len(t2)

a = [0] * 100001
a[0] = len(s)
for i in range(1, 100001):
    a[i] = min(2 * 10**18, l0 + l1 + l2 + a[i - 1] * 2)

def dfs(n: int, k: int) -> str:
    if k > a[n]:
        return '.'
    if n == 0:
        return s[k - 1]

    if k > l0 + a[n - 1] + l1 + a[n - 1]:
        return t2[k - (l0 + a[n - 1] + l1 + a[n - 1]) - 1]
    elif k > l0 + a[n - 1] + l1:
        return dfs(n - 1, k - (l0 + a[n - 1] + l1))
    elif k > l0 + a[n - 1]:
        return t1[k - (l0 + a[n - 1]) - 1]
    elif k > l0:
        return dfs(n - 1, k - l0)

    return t0[k - 1]

q = int(input())
ans = ''
for _ in range(q):
    n, k = map(int, input().strip().split())
    ans += dfs(n, k)

print(ans)

#include <iostream>
#include <vector>

using namespace std;
using ll = long long;

const int N = 100001;

ll a[N];
string s = "DKER EPH VOS GOLNJ ER RKH HNG OI RKH UOPMGB CPH VOS FSQVB DLMM VOS QETH SQB";
string t0 = "DKER EPH VOS GOLNJ UKLMH QHNGLNJ A";
string t1 = "AB CPH VOS FSQVB DLMM VOS QHNG A";
string t2 = "AB";
int l0 = t0.size();
int l1 = t1.size();
int l2 = t2.size();

char dfs(int n, ll k) {
    if (k > a[n]) {
        return '.';
    }
    if (n == 0) {
        return s[k - 1];
    }

    if (k > l0 + a[n - 1] + l1 + a[n - 1]) {
        return t2[k - (l0 + a[n - 1] + l1 + a[n - 1]) - 1];
    } else if (k > l0 + a[n - 1] + l1) {
        return dfs(n - 1, k - (l0 + a[n - 1] + l1));
    } else if (k > l0 + a[n - 1]) {
        return t1[k - (l0 + a[n - 1]) - 1];
    } else if (k > l0) {
        return dfs(n - 1, k - l0);
    } else {
        return t0[k - 1];
    }
}

int main() {
    a[0] = s.size();
    for (int i = 1; i < N; i++) {
        a[i] = min((ll)2E18, l0 + l1 + l2 + a[i - 1] * 2);
    }

    int q;
    cin >> q;

    string ans = "";
    while (q--) {
        int n;
        ll k;
        cin >> n >> k;
        ans += dfs(n, k);
    }

    cout << ans << "\n";

    return 0;
}

01 迷宫

OJ：洛谷

题意：给定一个 $n\times n\ (1\le n\le 1000)$ 的 01 方阵，询问 $m\ (1\le m\le 10^5)$ 次，每次询问从 $i,j\ (1\le i,j\le n)$ 出发可以移动多少格。移动规则为：可以走到曼哈顿距离为 $1$ 且与当前数值不同的四个格子中。

思路：

一道入门级网格图遍历问题，放在这主要是为了熟悉连通分量的概念以及 DFS、BFS 和 DSU 在这类问题上的板子写法；
回到本题，显然不可能问一次遍历一次，考虑预处理。预处理就直接遍历网格图同时标记每一个连通分量的大小即可。这里有一个遍历的小 trick，在遍历时保留走过的路径，遍历结束后给走过的路径全都赋上连通分量的大小即可，即二次遍历；
本题也可以用并查集实现，通过给每一个结点添加一个「大小域」来维护每一个结点所在连通分量的结点个数，相较于上述二次遍历策略，时间上的常数会小一点。

时间复杂度：$O(n^2)$

Python BFSPython DSUC++ DFS

from collections import deque

n, m = map(int, input().strip().split())
g = [""] * n
for i in range(n):
    g[i] = input().strip()

ans = [[0] * n for _ in range(n)]
vis = [[False] * n for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]

def bfs(i: int, j: int) -> None:
    cnt = 0
    path = []
    q = deque()

    cnt += 1
    path.append((i, j))
    vis[i][j] = True
    q.append((i, j))
    while q:
        x, y = q.popleft()
        for k in range(4):
            nx, ny = dx[k] + x, dy[k] + y
            if nx < 0 or nx >= n or ny < 0 or ny >= n:
                continue
            if vis[nx][ny] or int(g[x][y]) ^ int(g[nx][ny]) == 0:
                continue
            cnt += 1
            path.append((nx, ny))
            vis[nx][ny] = True
            q.append((nx, ny))

    for x, y in path:
        ans[x][y] = cnt

for i in range(n):
    for j in range(n):
        if not vis[i][j]:
            bfs(i, j)

for _ in range(m):
    i, j = map(int, input().strip().split())
    print(ans[i - 1][j - 1])

from collections import deque

class DSU:
    def __init__(self, n: int) -> None:
        self.n = n
        self.sz = n
        self.p = [i for i in range(n)]
        self.cnt = [1 for i in range(n)]

    def find(self, x: int) -> int:
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def merge(self, a: int, b: int) -> None:
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            self.p[pa] = pb
            self.cnt[pb] += self.cnt[pa]
            self.sz -= 1

    def same(self, a: int, b: int) -> bool:
        return self.find(a) == self.find(b)

    def size(self) -> int:
        return self.sz

    def size(self, a: int) -> int:
        return self.cnt[self.find(a)]

n, m = map(int, input().strip().split())
g = [""] * n
for i in range(n):
    g[i] = input().strip()

dsu = DSU(n * n)
vis = [[False] * n for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]

def bfs(i: int, j: int) -> None:
    q = deque()
    vis[i][j] = True
    q.append((i, j))

    while q:
        x, y = q.popleft()
        for k in range(4):
            nx, ny = dx[k] + x, dy[k] + y
            if nx < 0 or nx >= n or ny < 0 or ny >= n:
                continue
            if vis[nx][ny] or int(g[x][y]) ^ int(g[nx][ny]) == 0:
                continue

            dsu.merge(x * n + y, nx * n + ny)

            vis[nx][ny] = True
            q.append((nx, ny))

for i in range(n):
    for j in range(n):
        if not vis[i][j]:
            bfs(i, j)

for _ in range(m):
    i, j = map(int, input().strip().split())
    i -= 1
    j -= 1
    print(dsu.size(i * n + j))

#include <iostream>
#include <vector>

using namespace std;

const int N = 1010;

int n, m;
string g[N];
int ans[N][N];
bool vis[N][N];

int cnt;
vector<pair<int, int>> path;
int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};

void dfs(int i, int j) {
    path.push_back({i, j});
    vis[i][j] = true;
    cnt += 1;
    for (int k = 0; k < 4; k++) {
        int nx = i + dx[k], ny = j + dy[k];
        if (nx < 0 || nx >= n || ny < 0 || ny >= n || 
            vis[nx][ny] || (g[nx][ny] - '0') ^ (g[i][j] - '0') == 0) {
            continue;
        }
        dfs(nx, ny);
    }
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> g[i];
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (vis[i][j]) {
                continue;
            }
            cnt = 0;
            path.clear();
            dfs(i, j);
            for (auto& [x, y]: path) {
                ans[x][y] = cnt;
            }
        }
    }

    while (m--) {
        int i, j;
        cin >> i >> j;
        cout << ans[i - 1][j - 1] << "\n";
    }

    return 0;
}

同类题推荐：

登山 | 第 16 届蓝桥杯 Python A 组倒数第二题

随机排列

OJ：AcWing

题意：现在将一个含有 $n\ (2\le n\le 10^6)$ 个数的自然排列（即升序序列）进行 $3n$ 次或 $7n+1$ 次的对换操作，问是对换了 $3n$ 次还是 $7n+1$ 次，若是前者输出 $1$，后者输出 $2$。

思路：

一看到排列对换，立刻想到一个结论：在排列中进行一次对换操作，排列的逆序数的奇偶性就会发生一次变化；
容易发现 $3n \equiv n \pmod 2,7n+1 \equiv n+1 \pmod 2$，因此两种对换次数下，排列的逆序数的奇偶性是不一样的，这就可以成为区分两种对换次数的判别依据。即若 $n$ 为偶数，则对换 $3n$ 次后排列的逆序数一定是偶数，对换 $7n+1$ 次后排列的逆序数一定是奇数，反之同理；
发现了上述性质后，本题就变成了求序列逆序数的板子题。可以借助归并排序的分治思想求解。

时间复杂度：$O(n \log n)$

PythonC++

n = int(input().strip())
a = list(map(int, input().strip().split()))

def merge_sort(l: int, r: int) -> int:
    if l >= r:
        return 0

    # divide
    mid = (l + r) >> 1

    # conquer
    ans = merge_sort(l, mid) + merge_sort(mid + 1, r)

    # combine
    t = []
    i, j = l, mid + 1
    while i <= mid and j <= r:
        if a[i] <= a[j]:
            t.append(a[i])
            i += 1
        else:
            t.append(a[j])
            j += 1
            ans += mid - i + 1  # 点睛之笔
    while i <= mid:
        t.append(a[i])
        i += 1
    while j <= r:
        t.append(a[j])
        j += 1
    a[l:r+1] = t

    return ans

cnt = merge_sort(0, n - 1)

if n & 1:
    print(1 if cnt & 1 else 2)
else:
    print(2 if cnt & 1 else 1)

#include <iostream>
#include <vector>

using namespace std;
using ll = long long;

const int N = 1000010;

int n;
int a[N];

ll merge_sort(int l, int r) {
    if (l >= r) {
        return 0;
    }

    // divide
    int mid = (l + r) >> 1;

    // conquer
    ll ans = merge_sort(l, mid) + merge_sort(mid + 1, r);

    // combine
    int i = l, j = mid + 1;
    vector<int> t;
    while (i <= mid && j <= r) {
        if (a[i] <= a[j]) {
            t.push_back(a[i++]);
        } else {
            t.push_back(a[j++]);
            ans += mid - i + 1;  // 点睛之笔
        }
    }
    while (i <= mid) {
        t.push_back(a[i++]);
    }
    while (j <= r) {
        t.push_back(a[j++]);
    }
    for (int k = l, idx = 0; k <= r; k++) {
        a[k] = t[idx++];
    }

    return ans;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    ll cnt = merge_sort(0, n - 1);

    if (n & 1) {
        cout << (cnt & 1 ? 1 : 2) << "\n";
    } else {
        cout << (cnt & 1 ? 2 : 1) << "\n";
    }

    return 0;
}